Software: FEM - Tutorial - 2D-Bauteil - Vergleichsspannung
Vergleichsspannung
Entsprechend unserer Solver-Konfiguration wurde für die Spannungsberechnung die Gestaltänderungsenergiehypothese (GEH) genutzt und damit die sogenannte Mises-Vergleichsspannung ermittelt. Verfügbar sind die berechneten Spannungswerte in [MPa] an den Eckknoten, über Elemente gemittelt und in den sogenannten Gaußpunkten. Diese Werte werden wir in der unverformten Darstellung nacheinander betrachten.
Legende
- Die Anzahl der Stufen=11 und die Position in der linken oberen Ecke des Grafikfensters sind festgelegt.
- Die Farbzuordnung zu den einzelnen Stufen könnte man ändern (Menü: Ansichten > Farben > Legendenfarben), was aber kaum erforderlich sein dürfte (Standard: Min.Wert=blau ... Max.Wert=rot)
- Ungewohnt ist die Orientierung der Skale (Oben=Minimum / Unten=Maximum)
- Nach Aufruf der Postprozessor-Ansicht wird die Legende standardmäßig mit den aktuellen Minimal- und Maximal-Werten der gewählten physikalischen Größe skaliert.
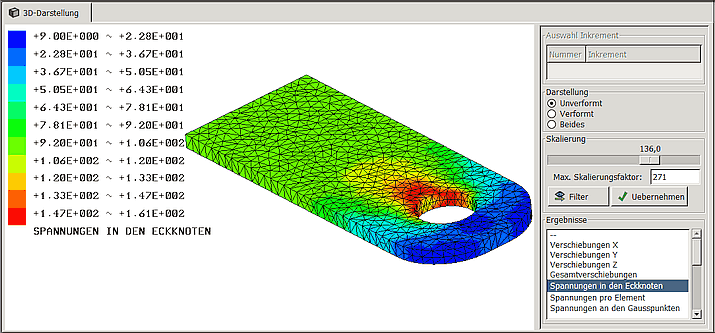
Eckknoten-Spannungen
- Die Legende ist mit den Min-/Max-Werten skaliert:
- Die maximale Knotenspannung von 161 MPa tritt am fixierten Lochrand auf. Diesen Wert kann man somit auch als Ergebniswert des Lochwand-Knotensets ablesen (Siehe: Auflagereaktionen).
- Die Farbkontur auf dem Oberflächennetz wird dargestellt als interpolierter Farbverlauf zwischen den Knotenfarben. Dies wirkt ästhetisch, gestattet jedoch nur eine qualitative Beurteilung und retuschiert Artefakte infolge ungünstiger Vernetzung.
- Die Spannungen werden in den Elementen nicht direkt für die Eckknoten berechnet, sondern für die Gauß-Punkte, welche in der Nähe der jeweiligen Eckknoten liegen.
- Da meist an einem Eckknoten mehrere Elemente anschließen, ergibt sich eine Eckknoten-Spannung dann als Interpolation zwischen den Gauß-Punkten der benachbarten Elementen. Dies führt zu recht ausgeglichenen Spannungsverläufen, die im Mittel aber geringer sind als die Maximalspannungen aus den Gauß-Punkten.
Mittlere Element-Spannungen
- Es werden die Spannungen in den Gauß-Punkten im jeweiligen Element berechnet, aufsummiert und durch die Anzahl der Gauß-Punkte geteilt. Dies ergibt die mittlere Vergleichsspannung pro Element:
- Es erfolgt keine Glättung der Farbkontur. Jedes Element erhält die zu seinem gemittelten Spannungswert passende Farbe aus dem Legenden-Wertebereich.
- Aufgrund der Mittelwertbildung ist die Maximalspannung geringer sein als die maximale Gaußpunkt-Spannung.
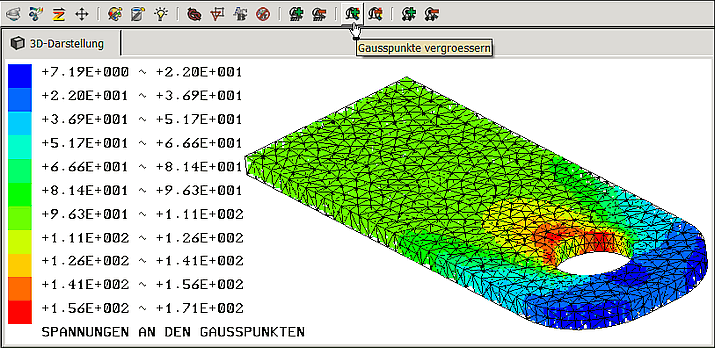
Gaußpunkt-Spannungen
- Am präzisesten ist die Spannungsanzeige direkt in den Gauß-Punkten. Es werden die Spannungen für genauso viele Gauß-Punkte berechnet, wie Eckknoten vorhanden sind.
- Um eine "homogen" gefüllte Farbkontur zu erhalten, muss man die Darstellungsgröße der Gaußpunkte optimal einstellen:
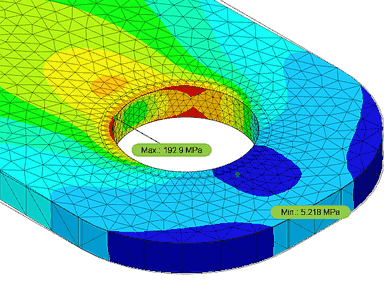
- Der max. Spannungswert von 171 MPa wurde direkt in einem Gauß-Punkt berechnet. Dieser Wert kann trotzdem falsch sein, wenn die Netzqualität an dieser Stelle unzureichend ist!
Berechnete Spannungswerte
- Die Datei z88o3.txt enthält für jedes Element die Positionen der Eck-Knoten [mm] und die Spannungen [MPa] an den zugehörigen Gauß-Punkten:
: Element # = 1156 Typ = 10-K Tetraeder XX YY ZZ SIGXX SIGYY SIGZZ TAUXY TAUYZ TAUZX SIGV +5.65E+00 +1.54E+00 +9.32E-01 +1.257E+02 -1.381E+01 -2.506E+00 -2.739E+01 +3.754E+00 +1.102E+00 +1.426E+02 +5.82E+00 +1.33E+00 +9.32E-01 +1.767E+02 -2.128E+00 +2.360E+01 -1.505E+01 -9.895E+00 +4.534E+00 +1.705E+02 +5.51E+00 +1.33E+00 +7.11E-01 +1.371E+02 -3.761E+00 +1.897E+00 -2.376E+01 -7.074E-01 +3.109E+00 +1.442E+02 +5.70E+00 +1.16E+00 +9.32E-01 +1.584E+02 -6.932E+00 +1.088E+01 -1.454E+01 -8.793E+00 +9.478E+00 +1.607E+02 :
- Die Struktur dieser Datei sieht man beispielhaft am Tetraeder-Element Nr. 1156 mit seinen 4 Eck-Knoten.
- Die Spalte SIGV enthält am letzten Gauß-Punkt den Maximalwert der Vergleichsspannung von "+1.607E+02" (gerundet 171 MPa).
- Dieser Wert stimmt recht gut überein mit dem Ergebnis entlang der Lochkante aus der Autodesk-Fusion-Studie:
Vernetzungsfeinheit
- Infolge der groben Vernetzung des Lochrandes im Z88Aurora zeigt sich nicht die Spannungsüberhöhung direkt an der Kante!
- Mit unserem Vorwissen, dass dieser Spannungswert an einer "ideal" eckigen Kante gegen Unendlich konvertiert, könnten wir auf eine Tetraeder-Verfeinerung am Lochrand verzichten. Diese wäre in Hinblick auf die Ergebnis-Genauigkeit sinnvoll, wenn die Befestigung der Lasche am Loch sowohl geometrisch als auch kontaktmäßig im Modell realistischer nachgebildet wird.
- Hinweis: Wir werden die lokale Netzverfeinerung im weiteren Verlauf dieses Übungskomplexes trotzdem noch durchführen, um das Prinzip der Tetraeder-Verfeinerung im Z88Aurora zu verstehen.