Software: SimX - Nadelantrieb - Aktordynamik - Magnetkreis
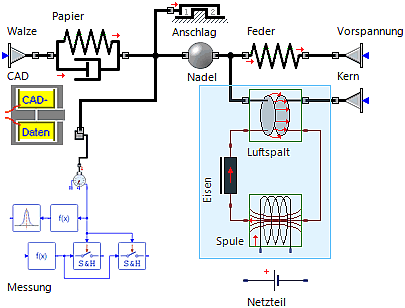
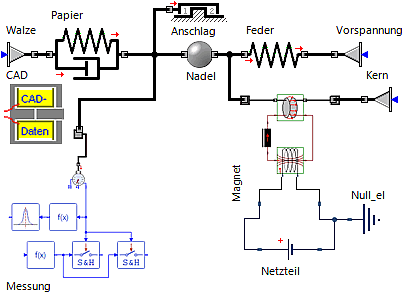
Netzwerkstruktur eines Elektromagneten
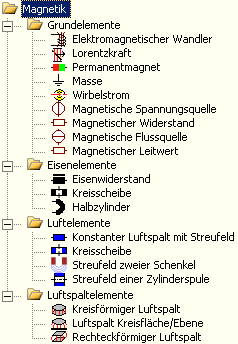
- Die Magnetik-Bibliothek enthält alle Element-Typen, um damit das Dynamik-Modell unseres Elektro-Magneten aufzubauen. Für jeden Element-Typ steht über die Taste <F1> eine ausführliche Beschreibung der implementierten physikalischen Zusammenhänge zur Verfügung.
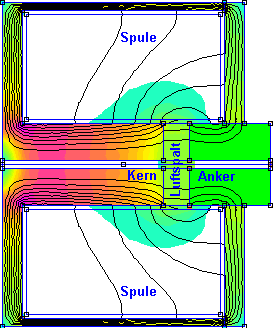
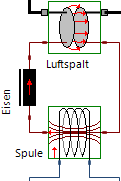
- Mit Elementen der Magnetik-Domäne können wir das magnetische Feld des Elektro-Magneten als magnetisches Netzwerk abbilden. Grundlage für die Wahl einer geeigneten Netzwerk-Struktur sind die "Wege" des magnetischen Flusses im realen Magnetkreis. Als Ersatz für den realen Magnetkreis (der häufig noch nicht existiert!), kann man die Finite-Element-Simulation benutzen. Diese berechnet die räumliche Struktur des Magnetfeldes. Im folgenden Bild ist die räumliche Verteilung der magnetischen Flussdichte B in einem Topfmagneten als Farbverlauf abgebildet (violett: B≥1 T / weiß: fast feldfrei):
- Man erkennt deutlich, dass nur der dem Arbeitsluftspalt abgewandte Teil des Magnetkerns (Eisen_innen) vom kompletten Spulenfluss durchflossen wird. Dort sollte man die magnetische Durchflutung (MMK) der Spule als konzentriertes Netzwerk-Element platzieren.
- Nur ein Teil des Flusses geht durch den äußeren Eisenkreis (Kernabschnitt2, Anker, Topf = Eisen_aussen) mit dem Arbeits-Luftspalt, der andere Teil des Flusses erstreckt sich durch den Luftraum der Spule (Spulenstreufeld).
- Infolge der unterschiedlichen Flussdichten "bewegen" sich die Eisenabschnitte auf unterschiedlichen Punkten ihrer µ(B)-Kennlinie. Das Eisen besitzt an jedem Ort und zu jedem Zeitpunkt individuelle Permeabilität.
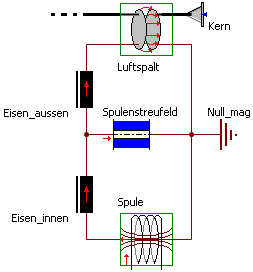
Die soeben beschriebenen Flusswege lassen sich nicht scharf abgrenzen. Trotzdem kommt man über diese Vereinfachung zu einer sehr einfachen Netzwerk-Struktur für Elektromagnete (noch nicht erzeugen!):
Vorbereitungen zur Compound-Definition (Teilmodell des Elektromagneten)
Am Beispiel des Signalprozessors haben wir bereits etwas Erfahrung bei der Compound-Definition mittels des SimulationX-TypeDesigners gesammelt. Diese Erfahrung werden wir nun am Beispiel des Elektromagneten vertiefen:
- Im Rahmen der Express Edition von SimulationX stehen uns nur noch wenige Elemente innerhalb des Modells zur Verfügung, bis wir das Maximum von 16 Elementen ausgeschöpft haben.
- Wir wählen hier eine Vorgehensweise, welche sich auch für die Vollversion von SimulationX vor dem "Zusammenfassen" als sinnvoll erweist:
- Definition aller Elemente des Teilmodells, welche Anschlüsse für Verbindungen zum Modell bereitstellen, in unserem Beispiel:
- "Luftspalt" mit den mechanischen Anschlüssen des magneto-mechanischen Wandlers
- "Spule" mit den elektrischen Anschlüssen des elektro-magnetischen Wandlers
- Definition aller konstruktiven Entwurfsgrößen für das Teilmodell innerhalb des "CAD_Daten"-Interface (hier: Maß- und Bauelement-Parameter)
- Definition aller Elemente einer abstrahierten Grundstruktur des Teilmodells zur Nutzung der automatischen Bilderstellung des TypeDesigners (hier: Luftspalt-, Eisen- und Spulen-Element)
- Definition aller Elemente des Teilmodells, welche Anschlüsse für Verbindungen zum Modell bereitstellen, in unserem Beispiel:
Arbeitsluftspalt
Der Arbeitsluftspalt ist der Luftspalt zwischen beweglichem Anker und festem Kern. In diesem Luftspalt entsteht die Kraft an den Trennflächen im magnetischen Feld. Er repräsentiert den magneto-mechanischen Wandler:
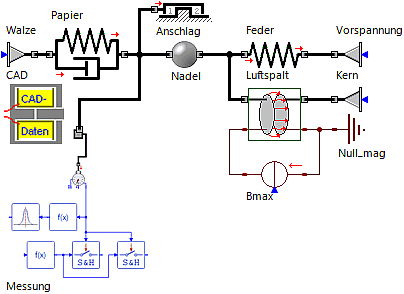
- Wir ersetzen im Modell das bisherige Kraftelement mit dem zugehörigen Impulsgenerator (beide Elemente löschen) durch die mechanische Seite das Magnetik-Luftspaltelement > Kreisförmiger Luftspalt:
- Wichtig: Die positive Richtung des magnetischen Flusses in den Magnetik-Elementen wird durch die roten Pfeile repräsentiert. Die Elemente sind vor dem Verbinden unter Beachtung ihrer positiven Flussrichtungen zu drehen/spiegeln!
- Um die Funktionsfähigkeit des "Luftspaltes" zu überprüfen, erzeugen wir darin die maximal zulässige Flussdichte Bmax-zul → daraus muss sich dann die bisher genutzte maximal mögliche Kraft Fmax ergeben.
- Dafür benötigen wir temporär das Magnetik-Grundelement > Magnetische Flussdichte.
- Der magnetische Kreis benötigt (wie jede physikalische Domäne) sein eigenes Null-Potential (Magnetik-Grundelement > Masse).
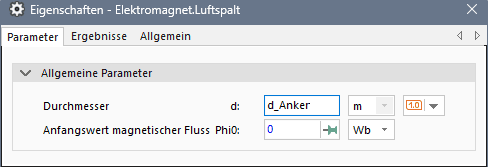
Zum Erzeugen der "konstanten" maximal möglichen Magnetkraft Fmax konfigurieren wir die beiden Magnetik-Elemente wie folgt:
- Als Durchmesser der Luftspaltfläche verwenden wir d=CAD.d_Anker.
- Der Anfangswert des magnetisches Flusses ist standardmäßig fixiert
 auf Phi0=0 Wb. Diese Fixierung des Anfangswertes ist zu entfernen
auf Phi0=0 Wb. Diese Fixierung des Anfangswertes ist zu entfernen  , da deren Wert bereits durch die Flussquelle bestimmt wird!
, da deren Wert bereits durch die Flussquelle bestimmt wird! - Die Flussquelle soll unter Berücksichtigung des aktuellen Ankerdurchmessers einen magnetischen Fluss erzeugen, welcher der maximal zulässigen Flussdichte im Eisen entspricht:
Magnetischer Fluss Phi_scr: CAD.A_Anker*CAD.Bmax_zul in Wb
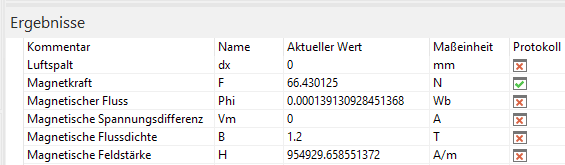
- Nach der Simulation muss sich bei der aktuellen Konfiguration Luftspalt.dx=0 mm ergeben. Die zugehörige Magnetkraft Luftspalt.F sollte auf ca. 1 Promille genau dem analytisch berechneten Wert CAD.Fmax entsprechen:
- Wichtig: Falls Luftspalt.dx nicht den Wert Null besitzt, muss man die Position der feststehenden Kern-Fläche korrigieren!
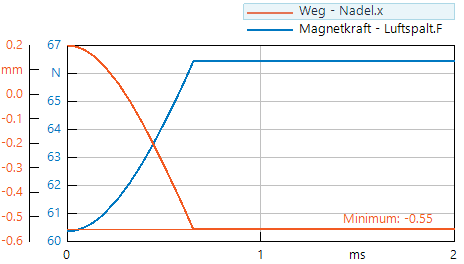
Interessant ist der zeitliche Verlauf der "konstanten" Magnetkraft beim Anzugsvorgang:
- Trotz konstanter Flussdichte ist die Kraft im Arbeitsluftspalt umso geringer, je größer Luftspalt.dx ist! Erst bei dx=0 wird der analytisch berechnete Wert von Fmax erreicht.
- Dieser Effekt resultiert aus der wirklichkeitsnäheren Modellierung des Luftspalt-Elementes, indem darin auch das tonnenförmige Streufeld berücksichtigt wird (nicht nur Feld im Kreis-Zylinder zwischen den Flächen!).
- Die Details zur Modellierung findet man unter Hilfe zum Bibliothekselement (Taste F1).
Restluftspalt eines Elektromagneten:
- Für die Verifizierung der richtigen Funktion des Luftspalt-Elementes nutzten wir bisher einen Restluftspalt dx=0 mm!
- Bei einem realem Elektromagneten würde damit der Anzugsvorgang ebenfalls funktionieren, obwohl es in Hinblick auf Verschleiß und Geräuschentwicklung ungünstig wäre. Allerdings gibt es dann beim Abfallvorgang Probleme, weil infolge der immer vorhandenen Hysterese nach dem Abschalten eine Remanenz-Feldstärke erhalten bleibt, so dass der magnetische Fluss im Luftspalt nicht Null wird.
- Bei einem Elektromagneten muss man konstruktive Lösungen finden, welche einen Restluftspalt (z.B. 50 µm) bei geschlossenem Arbeitsluftspalt garantieren.
- Wir ergänzen zum Testen diesen Restspalt vorläufig als Zahlenwert 50e-6 im Parameter der Kern-Wegvorgabe (bevor wir nachher diese Entwurfsgröße in CAD_Data ergänzen):
Weg x: CAD.x_Matrix + CAD.d_Praegung - 50e-6 in m
- Nach der Simulation ergibt sich dann das Ergebnis Luftspalt.dx=50 µm. Der Restspalt hat keinen Einfluss auf die Anschlagsposition -0,55 mm!
- Wichtig: Bevor wir im folgenden Schritt die CAD-Daten bereinigen, löschen wir im Modell die Flussquelle, weil diese zu löschende CAD-Daten benötigt!
Konstruktive Entwurfsparameter des Elektromagneten
- Vom CAD-Element sollen möglichst alle von Geometrie, Stoff und Zukauf-Bauteilen abhängigen Parameter für die idealisierten Netzwerk-Elemente des Modells bereitgestellt werden.
- Damit können diese Entwurfskenngrößen des Magnetantriebes an zentraler Stelle geändert werden und die Auswirkungen werden automatisch im gesamten Modell berücksichtigt.
- Wir nehmen in einer neuen Näherung an, das L_Anker dem Wert von d_Anker entspricht. Der in Etappe1 verwendete L_Faktor kann also entfallen.
- Der Kern soll doppelt so lang sein, wie der Anker. Das ergibt sich aus dem Vorwissen zur günstigen Lage des Arbeitsluftspalts innerhalb der Spule.
- Die nicht mehr benötigten Parameter und Variablen sind zu löschen:
- Abschaltung
- L_Faktor
- Bmax_zul
- my0
- Fmax → zugehörige Berechnung danach im Verhalten ebenfalls löschen!
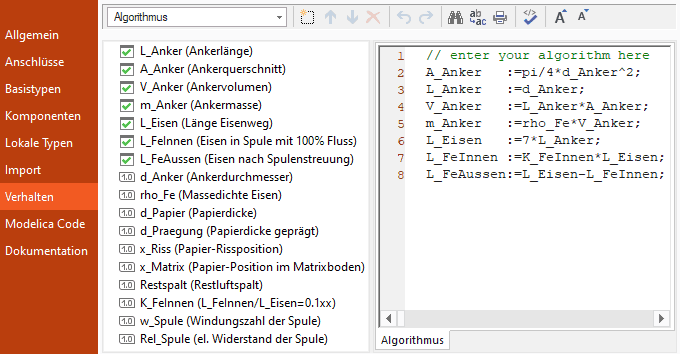
- Wir ergänzen die folgenden Größen im CAD_Data-Elementtyp:
Restspalt = 50 µm (Parameter: Restluftspalt im angezogenen Zustand) K_FeInnen = 0.1xx (Parameter: Verhältnis der Eisenwiderstände mit xx=Nr.) L_Eisen = 7 * L_Anker (Variable: Länge des Eisenweges) L_FeInnen = K_FeInnen * L_Eisen (Variable: Eisenabschnitt mit 100% Fluss) L_FeAussen = L_Eisen − L_FeInnen (Variable: restlicher Eisenabschnitt) w_Spule = 500 (Parameter: Windungszahl der Spule) Rel_Spule = 1 Ohm (Parameter: el. Widerstand der Spule)
- Mit den CAD-Werten müssen innerhalb des Modells folgende Element-Parameter gespeist werden:
Nadel.m = 0.001 + CAD.m_Anker (bereits in Etappe1 erfolgt) Anschlag.l2 = abs(CAD.x_Matrix + CAD.d_Praegung) (bereits in Etappe1 erfolgt) Kern.x = CAD.x_Matrix + CAD.d_Praegung - CAD.Restspalt (zur Realisierung eines Restluftspalts)
- Die entsprechenden Element-Parameter innerhalb des noch zu bildenden Magnet-Compounds speisen wir später indirekt über die Compound-Parameter!
Abstrahierte Teilmodell-Struktur
Insbesondere als Anfänger sollte man möglichst die Automatismen nutzen, welche vom SimulationX-TypeDesigner beim Zusammenfassen von Elementen zu einem Compound bereitgestellt werden:
- Generierung der energetischen Kopplung mit dem übergeordneten Modell an der mechanischen Seite des Luftspalt-Elementes und der elektrischen Seite der Spule.
- Das automatisch generierte Bildsymbol kann im Beispiel die Komplexität der gesamten inneren Compound-Struktur nicht mehr abbilden. Wir definieren deshalb vor dem Zusammenfassen nur jeweils ein Element pro Compound-internem Teilsystem einschließlich der Verbindungen:
- Luftspalt: Arbeitsluftspalt als magneto-mechanischer Wandler (Magnetik > Luftspaltelemente > Kreisförmiger Luftspalt)
- Eisen: zur Bündelung des Magnetfeldes (Magnetik > Eisenelemente > Eisenwiderstand)
- Spule: Draht-Windungen um Eisenkreis (Magnetik > Grundelemente > elektromagnetischer Wandler)
- Die Elemente sind entsprechend zu verbinden, nachdem sie zuvor in die richtige Richtung gedreht wurden.
- Eine Parametrisierung ist noch nicht erforderlich.
- Um ein symmetrisches Struktur-Symbol zu erhalten (und die Begrenzungen der Express Edition einzuhalten), löschen wir die magnetische Masse vor dem Zusammenfassen.
- Netzteil: Gleichspannung zur elektrischen Energieversorgung (Elektrotechnik > Analog > Quellen >Spannungsquelle) verbinden wir mit der Spule, damit beim Zusammenfassen an dieser Stelle die elektrischen Anschlüsse generiert werden!
Elektromagnet-Compound
Express Edition - Workaround
Leider schlägt auch bei dieser Compound-Bildung die Beschränkung der Express Edition auf 16 Elemente innerhalb des Modells zu:
- Vor dem eigentlichen Zusammenfassen der markierten Elemente erzeugt der TypeDesigner innerhalb des aktuellen Modells automatisch die zusätzlich erforderlichen Anschlüsse für die Compound-Schnittstellen zum übergeordneten Modell.
- Diese zusätzlichen Anschlüsse werden mit den bereits markierten Elementen erst danach zum Compound zusammengefasst. Diesmal sind sogar vier zusätzliche Anschluss-Elemente erforderlich (zwei mechanische und zwei elektrische!).
- So erfolgt dann die Fehlermeldung zur Überschreitung der Anzahl der Elemente bei der Generierung der elektrischen Anschlüsse für die Schnittstelle zur Spule.
- Wir behelfen uns diesmal damit, dass wir auf die automatische Generierung dieser elektrischen Anschlüsse verzichten und diese dann nachher innerhalb des TypeDesigners manuell ergänzen.
Beachte:
- Bei Verwendung der Express Edition müssen vor dem Markieren der zusammenzufassenden Elemente die beiden Verbindungen zur Spannungsquelle gelöscht werden!
- Die Anleitung beschreibt im Folgenden die in der Express Edition notwendigen Schritte, welche man sich in der Vollversion ersparen kann.
Zusammenfassen der abstrahierten Teilmodell-Struktur
Bevor man über die Multifunktionsleiste den TypeDesigner zur Compound-Bildung aufrufen kann, muss man die drei Modell-Elemente markieren, welche zusammengefasst werden sollen.
Die gleichzeitige Markierung mehrerer Elemente erreicht man durch Rechteck-Auswahl mittels des Cursors bei gedrückter Maustaste (wie im Bild gezeigt). Ist dies auf Grund der Element-Anordnung nicht möglich, kann man Modell-Elemente durch zusätzlich betätigter UMSCHALT-Taste bei der Cursor-Markierung der Auswahl hinzufügen bzw. auch entfernen:
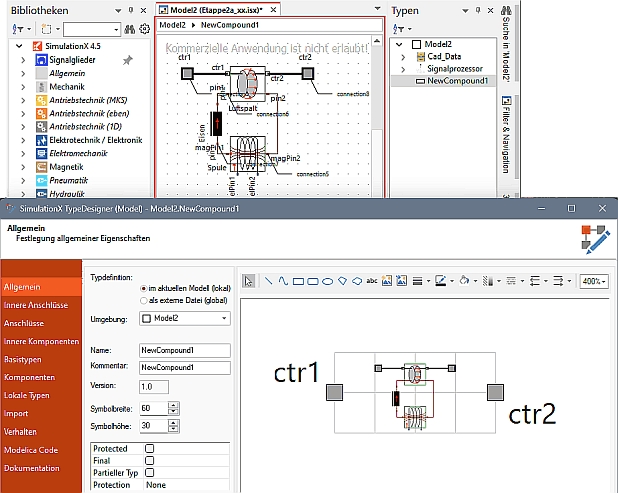
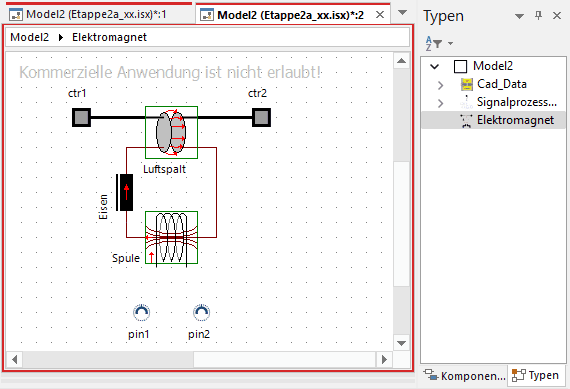
Nach Aufruf des TypeDesigners erscheint dieser im Bearbeitungsmodus für einen neuen Compound-Typ, welcher die markierten Modell-Elemente und deren Verbindungen enthält:
- Standardmäßig wird der neue Compound-Typ lokal im aktuellen Modell erzeugt und erscheint im Typen-Explorer (im Beispiel unter dem bereits vorhandenem Signalprozessor-Typ).
- Der grafische Editor des SimulationX enthält nun eine Ebene unter dem aktuellen Modell die Compound-Struktur, welche dort auch bearbeitet werden kann.
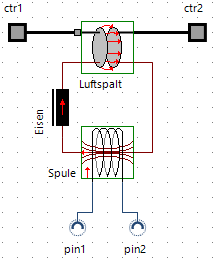
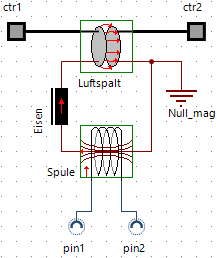
- Standardmäßig wird für den Compound-Typ ein Symbol der Größe 60x30 mm² erzeugt. Im zugehörigen Grafikeditor wird passend zu dieser Größe ein Strukturbild der zusammengefassten Elemente bereitgestellt.
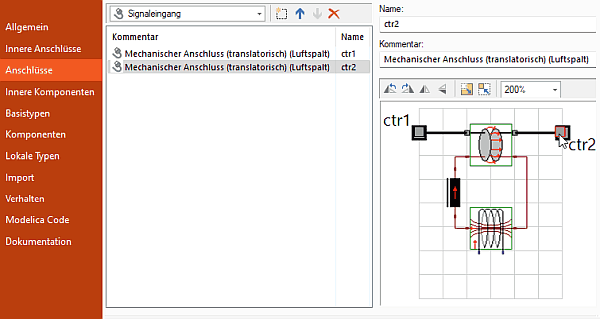
- Für die Verbindungen zwischen den Compound-Elementen und der Rest der Modellstruktur werden passende Schnittstellen generiert. Im Beispiel sind dies ctr1 und ctr2 (translatorische Mechanik-Konnektoren), welche die mechanischen Anschlüsse des Luftspalts nach außen führt.
- Wir orientieren uns wieder an den auf der linken Seite aufgelisteten Bearbeitungsschritten zur Typ-Definition.
Allgemein
Wir modifizieren hier Namen, Kommentar und Grafiksymbol:
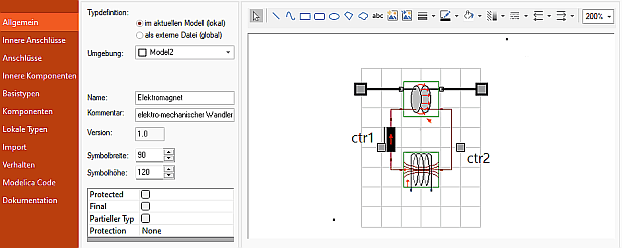
- Name: Elektromagnet
- Kommentar: elektro-mechanischer Wandler
- Symbol:
- Breite x Höhe: 90 Pixel x 120 Pixel (diese Verkleinerung auf ca. 60% ermöglicht Erkennbarkeit)
- Bild-Anpassung: nach Wahl eines geeigneten Zoom-Faktors im Symbol-Editor (z.B. 200 %) mittels Cursor an den 2 diagonalen Eckpunkten das sehr kleine Bild auf komplette Symbolgröße ziehen (Mechanik-Anschlüsse exakt an oberen Gitterpunkten beider Seitenkanten:
Anschlüsse
Die beiden Marker für die automatisch generierten mechanischen Anschlüsse muss man mit dem Cursor im Symbol-Editor auf die entsprechenden Positionen im Symbol-Bild schieben:
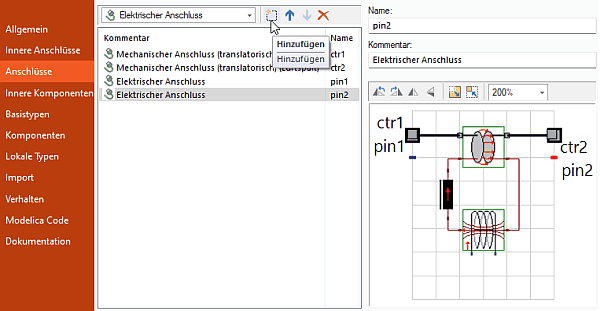
Die Express-Edition erfordert im Beispiel das manuelle Ergänzen der beiden benötigten elektrischen Anschlüsse einschließlich ihrer Verbindung mit den Spulen-Anschlüssen:
- Wir fügen zuerst im TypeDesigner die beiden elektrischen Anschlüsse hinzu, welche als pin1 und pin2 auch in der Symbolgrafik auftauchen:
- Die noch fehlenden Verbindungen zwischen den elektrischen Anschlüssen der Spule und den elektrischen Anschlüssen des Elektromagnet-Compound ergänzen wir später.
- Das von uns verwendete, automatisch generierte Compound-Strukturbild wird nur zum Zeitpunkt des Zusammenfassens erstellt. Spätere Modifikationen der inneren Struktur werden darin nicht berücksichtigt.
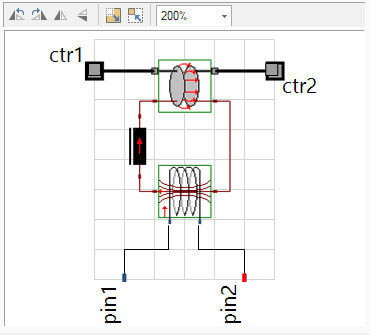
- Wir schieben deshalb die beiden elektrischen Pin mit dem Cursor an günstige Positionen.
- Danach nutzen den Grafikeditor im Abschnitt "Allgemein", um das Symbol manuell um die beiden Verbindungslinien zu ergänzen (Linienstärke 1 ½ pt / Linienfarbe schwarz). Dies ergibt danach folgende Ansicht im Abschnitt "Anschlüsse":
- Hinweise: Die Linienzüge erfordern jeweils einen Mausklick am Anfangs- und jeden Knickpunkt, sowie einen Doppelklick am Endpunkt. Misslungene Linien können markiert und dann gelöscht werden.
Wichtig → Speichern des Arbeitsstandes:
Wir haben schon einiges an Aufwand in die Bildung des Magnet-Compound investiert. Deshalb soll dieser Zwischenstand jetzt definiert auf dem Datenträger gespeichert werden:
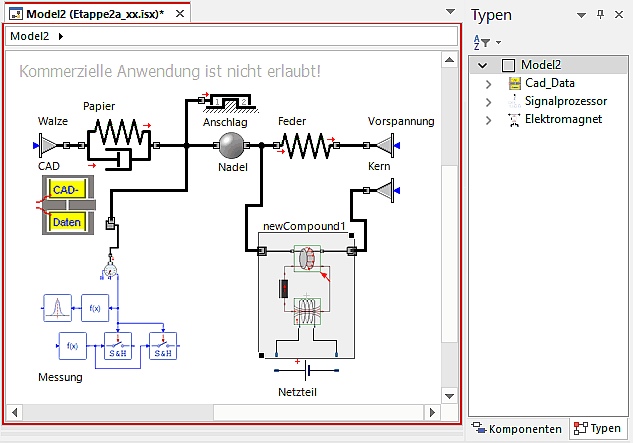
- TypeDesigner > Fertigstellen: schließt auch die Compound-Strukturansicht und zeigt das Compound-Element in der Modellstruktur als "NewCompound1" ("Elektromagnet" im Typen-Explorer):
- Magnet: als Name des Teilmodells im Modell eintragen
- Datei > Speichern: Bei der Erstellung dieser Anleitung behielt trotz "Speichern" das Modell den Stern als Markierung (nicht gespeicherte Änderungen enthalten?).
- Datei > Modell schließen und SimulationX beenden: führt zu einem definierten Abschluss dieses Bearbeitungszustandes.
- SimulationX starten und Datei öffnen > Etappe2a_xx.isx : ausgehend von diesem Zustand können wir den Magnet-Compound nun weiter bearbeiten.
Bevor wir weiter im TypeDesigner arbeiten öffnen wir über das Kontextmenü im Type-Explorer die Strukturansicht des Elektromagnet-Compound und ergänzen darin die noch fehlenden Verbindungen:
- Die beiden im TypeDesigner hinzugefügten elektrischen Anschlüsse müssen als erstes mit dem Cursor an sinnvolle Positionen verschoben und entsprechend gedreht werden:
- Die Beschriftung der Pin sollte unten angeordnet werden, um Platz für die Verbindungen zu schaffen. Die Verbindungen zu den Spulen-Anschlüssen selbst sind dann kein Problem mehr:
Die Änderungen in der Strukturansicht werden mit dem Bearbeitungszustand des im TypeDesigner synchronisiert. Leider ist nicht dokumentiert, wann diese Synchronisation erfolgt. Um wieder einen definierten Zustand zu erreichen, sollte man den Weg über das Speichern und Schließen des Modells gehen:
- Schließen der Strukturansicht ("X" am der Register): führt noch nicht zu einer Speicher-Abfrage.
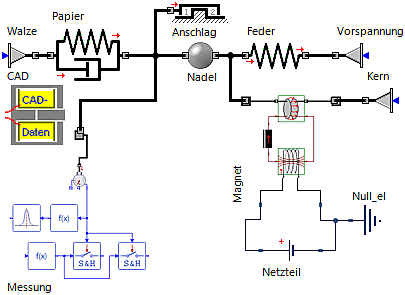
- Magnet-Compound mit Spannungsquelle verbinden und das erforderliche Nullpotential für die elektrische Domäne ergänzen (Elektrotechnik > Analog > Grundbausteine > Masse).
- Zusätzlich wurden die Elemente in der Modell-Strukturansicht ansprechend platziert:
- Datei > Speichern: danach Modell schließen und SimulationX neu starten
Wir haben damit den Workaround für die Begrenzungen der Express Edition abgeschlossen und können uns dem nächsten Abschnitt der Compound-Definition zuwenden.
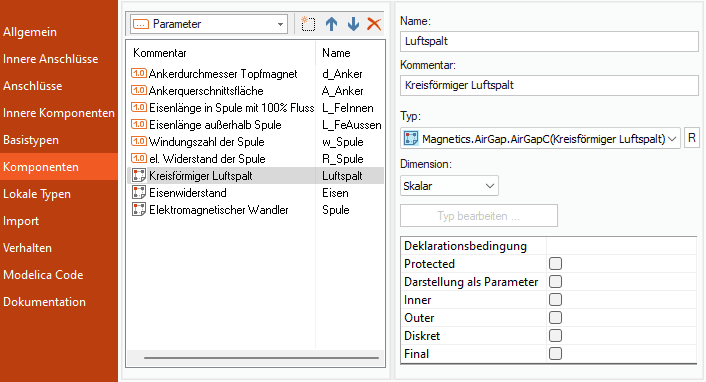
Komponenten-Definition (Parameter)
Für den Elektromagnet-Type öffnen wir wieder den TypeDesigner, welcher nun auch alle Änderungen enthält, die wir in der Strukturansicht vorgenommen hatten.
Parameter und Variable (Ergebnisse) des Komponenten-Abschnitts bilden die Datenschnittstelle zwischen den Elementen im Compound und der übergeordneten Modellebene.
- Innerhalb des Magnet-Compound müssen die Elemente der Magnetik-Domäne mit den entsprechenden Parametern gespeist werden, welche von den konstruktiven Entwurfsgrößen im CAD_Data-Element abgeleitet werden:
- Durchmesser, Querschnittsflächen und Längen der Eisen-Elemente, der Spulenstreuung und des Arbeitsluftspalts
- Windungszahl und ohmscher Widerstand der Spule
- Dafür sind im Komponenten-Abschnitt des Compound folgende Parameter mit sinnvoller Standardbelegung zu definieren (z.B.):
d_Anker = 10 mm : Ankerdurchmesser Topfmagnet A_Anker = 1 cm² : Ankerquerschnittsfläche L_FeInnen = 10 mm : Eisenlänge in Spule mit 100% Fluss L_FeAussen = 60 mm : Eisenlänge außerhalb Spule w_Spule = 500 : Windungszahl der Spule R_Spule = 1 Ohm : el. Widerstand der Spule
- Im Komponenten-Abschnitt sind bereits alle zum Compound zusammengefassten Modell-Elemente enthalten. Die später noch in der Struktur-Ansicht zu ergänzenden Modell-Elemente werden automatisch an das Ende der Komponentenliste gesetzt.
- Wir platzieren die erforderlichen neuen Parameter deshalb an den Anfang der Komponenten-Liste:
Bevor wir in die Strukturansicht des Magnet-Compounds wechseln, Speichern wir den erreichten Bearbeitungszustand:
- TypeDesigner > Fertigstellen
- Datei > Speichern
Struktur des Elektromagnet-Compound in der Strukturansicht vollenden
In der geöffneten Modelldatei öffnen wir für den Elektromagnet-Compound die Strukturansicht, um die "symbolische" Grundstruktur zur endgültigen Netzwerk-Struktur umzugestalten. Dabei können wir für die Parametrisierung die im Komponenten-Abschnitt definierten Schnittstellen-Parameter benutzen.
Magnetisches Null-Potential
- Jede physikalische Domäne in einem Netzwerk-Modell benötigt ein "Masse"-Element, welches den Knoten mit dem Potentialwert Null festlegt.
- Aus Gründen der Symbol-Übersichtlichkeit (und wegen der Beschränkungen der Express Edition) hatten wir die magnetische Masse vor dem Zusammenfassen der Compound-Elemente entfernt.
- Die feststehende Kernfläche des Luftspalts soll die magnetische Spannung Vm=0 A erhalten:
Arbeitsluftspalt
- Die magnetische Seite des magneto-mechanischen Wandlers ist innerhalb des Elektromagnet-Compounds Bestandteil der Magnetik-Domäne.
- Der Durchmesser d des Luftspalts muss mit dem Wert des Ankerdurchmessers d_Anker belegt werden:
Spule und Anfangswerte des magnetischen Flusses
- Der magnetische Kreis benötigt eine Quelle (MMK=Magneto-Motorische Kraft).
- Wir benutzen einen elektro-magnetischen Wandler in Form einer Spule.
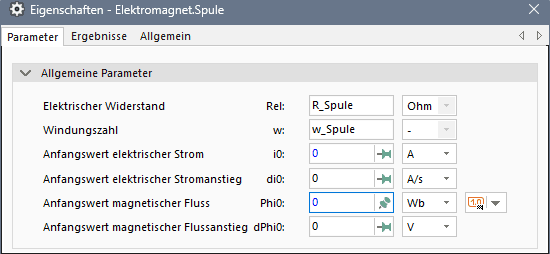
- Die Vorgabewerte von 500 Windungen bei 1 Ohm Drahtwiderstand ersetzen wir durch die Parameter-Werte von w_Spule und R_Spule.
- Wir fixieren den Anfangswert des magnetischen Flusses in der Spule auf Phi0=0 Wb. Damit ergeben sich die Anfangswerte für den magnetischen Fluss in allen anderen Elementen des Magnetkreises ebenfalls zu Phi0=0 Wb.
- Da der Magnetkreis keine zusätzlichen magnetischen Spannungsquellen (z.B. in Form von Wirbelstrom-Elementen) enthält, ist der Stromfluss in der Spule über die Beziehungen des elektromagnetischen Wandlers fest mit dem magnetischen Fluss gekoppelt. Aus dem fixierten Anfangswert Phi0=0 Wb ergibt sich also der Anfangswert des elektrischen Stromes in der Spule zu i0=0 A. Deshalb darf in der Spule der Wert von i0 nicht fixiert werden!
- Hinweis: Die Anfangswerte für die zeitlichen Ableitungen des Stromes di0 und des Flusses dPhi0 vertragen ebenfalls keine Fixierungen, weil sich ihre Werte aus den bekannten Zustandsgrößen ergeben.
Eisenmaterial und Eisen-Abschnitte (Innen und Aussen)
Bevor wir den gesamten Eisenwiderstand in zwei markante Abschnitte unterteilen, betrachten wir die Abhängigkeit der relativen magnetischen Permeabilität des Eisenmaterials µRel von der aktuellen magnetischen Flussdichte B:
- Mit den Eisen-Elementen werden standardmäßig die Materialkennwerte für Trafoblech 530-50 A mitgeliefert.
- Dieses wollen wir in Ermangelung eigener Kennwerte für unseren Magnetkreis verwenden.
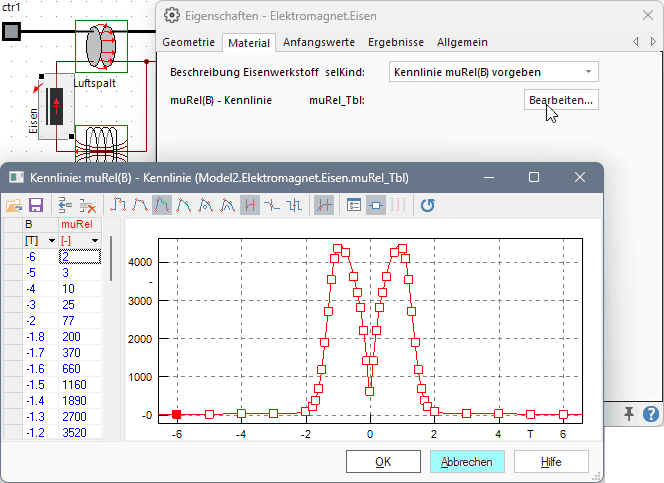
- Der Zugriff auf diese Werte kann über verschiedene Methoden erfolgen. Der Anschaulichkeit halber wählen wir den Zugang über die Kennlinie muRel(B). Auf diese kann man dann in der Material-Registerkarte mittels "Bearbeiten" zugreifen:
- Für die Flussdicht B=0 T beträgt im Beispiel die relative Anfangspermeabilität µRel=600.
- Steigt der Betrag |B| der Flussdichte (Symmetrie der Kurve um die Ordinatenachse!), so erreicht die rel. Permeabilität bei ca. B=1 T ihren Maximalwert µRel=4350 (Änderung fast ca. Faktor 7).
- Bei größeren B-Werten sinkt der Wert von µRel (insbesondere nach Überschreiten der Sättigungsflussdichte, im Beispiel ca. 2 T).
- Der Wert von µRel konvergiert bei noch größeren Flussdichten gegen 1. D.h., das Eisenmaterial nähert sich in seiner magnetischen Leitfähigkeit dem Wert von Luft.
- Wichtig:
Die vorgegebene Kennlinie muRel(B) entspricht nicht den Materialkennwerten für Trafoblech 530-50 A und sollte hier nur die qualitative Abhängigkeit der Permeabilität von der Flussdichte verdeutlichen! Deshalb muss man abschließend unbedingt für das Eisen-Material wieder Trafoblech 530-50 A wählen.
Die bisherige Netz-Struktur der magnetischen Domäne mit nur einem zylinderförmigen Eisenelement stellt eine extrem grobe "nullte" Näherung dar, wenn man das bereits bekannte Bild mit der realen räumliche Verteilung der magnetischen Flussdichte B in einem Topfmagneten als Farbverlauf betrachtet (violett: B≥1 T / weiß: fast feldfrei):
Eine verbesserte "erste" Näherung erhält man, wenn man den Eisenkreis in zwei zylinderförmige Abschnitte unterteilt:
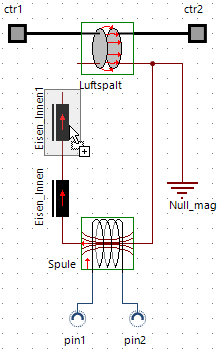
- "Eisen_innen": Teil des Magnetkerns innerhalb der Drahtspule, welcher "näherungsweise" vom kompletten Magnetfluss der Spule durchflossen wird. Dort wird auch die magnetische Durchflutung (MMK) der Spule als konzentriertes Netzwerk-Element platziert.
- "Eisen_aussen" (Kernabschnitt2, Anker, Topf): Ein Teil des Flusses strömt nicht durch den äußeren Eisenabschnitt, sondern verläuft durch den Luftraum der Spule (Spulenstreufeld). Den restlichen magnetischen Fluss leitet der äußere Eisenabschnitt durch den Arbeitsluftspalt.
Wir können sehr einfach den zweiten Eisenwiderstand ergänzen, einbinden und parametrisieren:
- Zuerst löschen wir die Verbindung zwischen dem jetzigen Eisenwiderstand und dem Luftspalt.
- Nach Umbenennung des vorhanden Eisenwiderstandes in "Eisen_Innen" (mit entsprechendem Kommentar) erhält er die zugehörigen Parameter:
Länge l : L_FeInnen Querschnittsfläche A : A_Anker Anfangswert magn. Fluss Phi0 : 0 Wb (nicht fixieren, da durch Spule vorgegeben)
- Wir schaffen Platz für den zweiten Eisenwiderstand, indem wir die Elemente unterhalb des Luftspalts in der Struktur weiter nach unten verschieben.
- Man könnte sich den zweiten Eisenwiderstand auch aus der Modellbibliothek herüberziehen. "Eleganter" funktionierte es bei gedrückter <Strg>-Taste durch Anklicken und Ziehen des in der Struktur vorhandenen Elements:
- Es wird dabei eine Kopie erzeugt, welche man an der gewünschten Position ablegt.
- Dabei kann auch bereits automatisch die Verbindung zum vorherigen Element hergestellt werden, wenn man beim Ziehen die zu verbindenden Anschlüsse übereinander hält.
- Falls diese Verbindung nicht oder falsch entsteht, muss man dies manuell korrigieren (im Bild fehlt z.B. noch die Verbindung zum Luftspalt).
- Erforderlich ist das Umbenennen in "Eisen_Aussen" mit Änderung des Kommentars
- Der Vorteil der Element-Kopie besteht auch in der vereinfachten Parametrisierung, da die komplette Konfiguration übernommen wird:
Länge l : L_FeAussen Querschnittsfläche A : A_Anker Anfangswert magn. Fluss Phi0 : 0 Wb (nicht fixieren, da durch Spule vorgegeben)
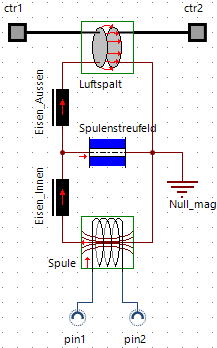
Spulenstreufeld
Das Magnetik-Element Luftelemente > "Streufeld einer Zylinderspule" berechnet den konstanten magnetischen Ersatzwiderstand, der nur von der Geometrie des Wicklungsraums der Spule abhängt:
Näherungsweise können wir in Bezug auf den Ankerdurchmesser d_Anker den Wickelraum vorläufig wie folgt beschreiben (dabei vernachlässigen wir die Wandstärken des Eisen-Topfes):
Innendurchmesser din : d_Anker Außendurchmesser dout : 2 * d_Anker Länge l : 3 * d_Anker Anfangswert magn. Fluss Phi0 : 0 Wb (nicht fixieren, da durch Flussteiler-Regel vorgegeben)
Nach dem Ergänzen der Spulenstreuung kann man die Magnet-Struktur noch etwas in Hinblick auf "Schönheit" zurechtzupfen, wobei man zum Verschieben des Null-Potentialknotens zuvor den kompletten Verbindungszug löschen muss:
Wichtig:
Den erarbeiteten Modellzustand sollte man nach Schließen der Compound-Strukturansicht Speichern. Das komplette Schließen und erneute Öffnen des Modells garantiert einen definierten Zustand.
Einspeisung der Entwurfsparameter im Magnet-Compound
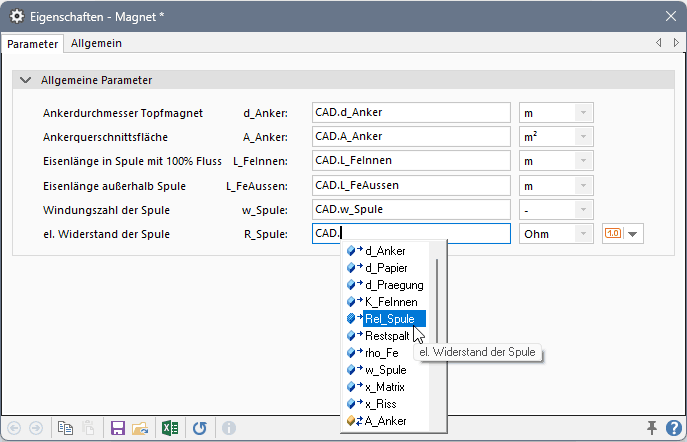
Innerhalb des Magnet-Compounds werden die Parameter (Komponenten) bereits an die einzelnen Elemente des Magnetkreises verteilt. Es fehlt jetzt noch die Einspeisung der CAD-Entwurfsparameter in die Parameter des Magnet-Compound:
Dies gestaltet sich sehr einfach, da nach Eingabe von "CAD." eine Liste aller verfügbaren CAD-Werte erscheint. Durch Doppelklick wählt man daraus die gewünschte Größe.
Validierung des Magnetkreis-Modells
Nach Fertigstellen des Magnet-Compound einschließlich der Parametrisierung fehlt nun noch ein entscheidender Schritt - die Validierung. Infolge der nichtlinearen magnetischen Eigenschaften des Eisenmaterials kann man die Glaubwürdigkeit des Modellverhaltens überwiegend nur qualitativ überprüfen. Für bestimmte definierte Anfangs- und Endzustände kann man die Richtigkeit der Werte jedoch auch quantitativ einschätzen.
Vor dem Start der Simulation nehmen wir noch folgende Einstellungen vor:
- tStop = 30 ms → Verlängerung der Simulationszeit (um eingeschwungenen Endzustand für den E-Magneten zu erreichen)
- Netzteil.V = 10 V → ergibt mit R_Spule = 1 Ohm einen Endstrom von 10 A.
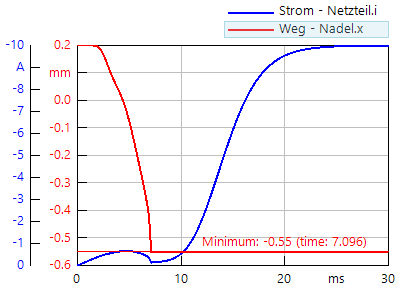
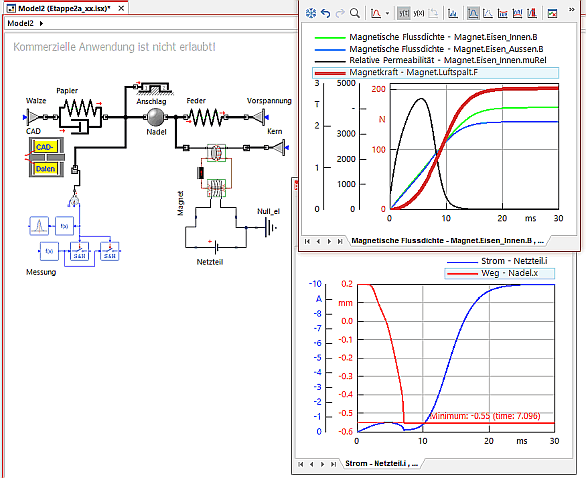
Nach der Simulation konfigurieren wir ein Ergebnisfenster mit dem Stromanstieg und dem Verlauf der Nadel-Bewegung:
- Bei positiver Spannung ergibt sich an dem Netzteil ein negativer Stromwert → deshalb für Y-Achse des Stroms "Negative Orientierung=True" setzen!
- Der Anker mit der Nadel verbleibt in der Ruhelage, solange die Magnetkraft kleiner ist, als die Rückstellkraft der Federvorspannung.
- Durch die Ankerbewegung entsteht in der Spule eine Gegeninduktionsspannung, welche dem Anstieg des Stromes entgegenwirkt und dann umkehrt.
- Nach dem plastischen Anschlag der Nadel auf dem geprägten Papier steigt der Strom wieder an bis zu seinem Endwert von 10 A.
- Die Magnetkraft drückt die Nadel dauerhaft auf das Papier, da im Modell keine Abschaltung vorgesehen wurde.
Um interne Größen eines Compound auf der Modellebene in einem Ergebnisfenster darzustellen, muss man sich in die Strukturansicht des betreffenden Compound begeben. Dafür stehen verschiedene Möglichkeiten zur Verfügung:
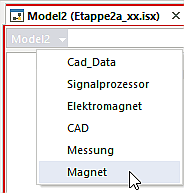
- Nach Klick auf den Hierarchiepfeil neben dem Modellnamen auf der Registerkarte öffnet sich eine Liste der möglichen Compounds. Hierbei muss man jedoch beachten, dass man nicht den Compound-Typen, sondern die im Modell verwendete Instanz wählt:
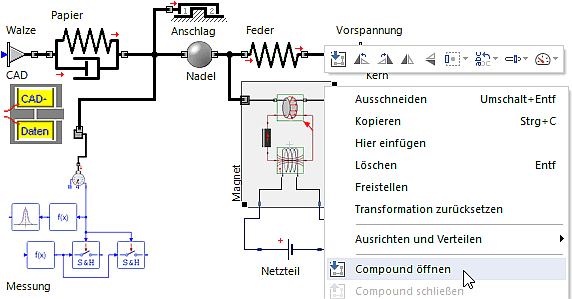
- Man kann über das Kontextmenü des Compound-Elements dessen Strukturansicht direkt öffnen:
- In der Strukturansicht des Compound ist der Hintergrund grau, wenn es sich um das Modell-Element handelt. Den Compound-Typen erkennt man am weißen Hintergrund!
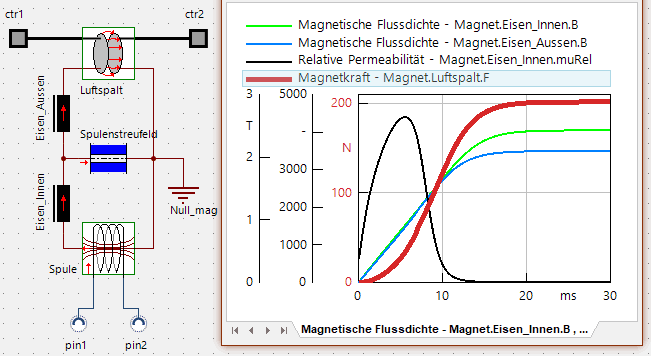
In der Strukturansicht des Magnet-Compound konfigurieren wir ein Ergebnisfenster mit:
- den magnetischen Flussdichten in den beiden Eisen-Abschnitten
- der relativen magnetischen Permeabilität (im inneren Eisenabschnitt)
- dem Kraftverlauf im Luftspalt:
- Die magnetische Flussdichte steigt näherungsweise linear in der Zeit → der Kraftanstieg ist deshalb am Anfang quadratisch.
- Die Flussdichte wird infolge der magnetischen Sättigung des Eisens begrenzt.
- Die Abzweigung des Gesamtflusses durch das Spulenstreufeld macht sich mit steigender Sättigung des Eisens stärker bemerkbar. Allerdings werden die in der Simulation erreichten Flussdichten von über 2 T in der Praxis kaum erreicht.
- Aus dem sehr großen Endwert der Flussdichte resultiert auch die eine wesentlich größere Haltekraft Fmax im Vergleich zu unseren vorherigen Annahmen.
Die Compound-Strukturansicht kann man auch schließen, indem man auf der Registerkarte die Modell-Ebene anklickt:
- Das in der Compound-Strukturebene konfigurierte Ergebnisfenster bleibt dabei geöffnet:
- Bei Bedarf könnte man die Signale der Compound-Ebene nachträglich durch Signale der Modell-Ebene ergänzen.