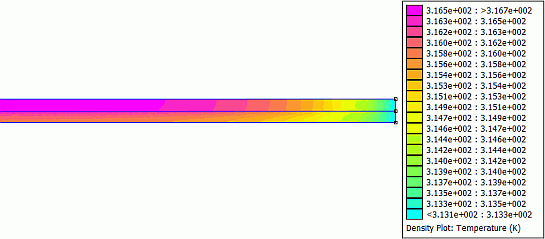Software: FEM - Tutorial - Feldkopplung - MP - Thermo-Bimetall - FEMM-Transiente Simulation

↑

← →

Transiente Simulation (FEMM - Heat Flow Problem)

Achtung: kein Bestandteil der FEM-Übung (nur zur Information)!

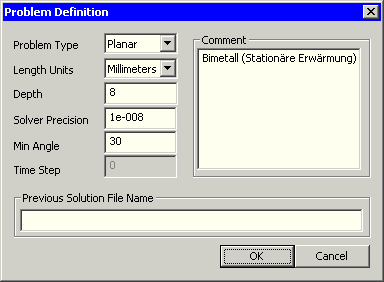
Das Programm FEMM ermöglichte ursprünglich nur die stationäre Berechnung von Wärmestrom-Problemen unter Berücksichtigung der Wärmeleitung, Konvektion und Strahlung. Inzwischen sind auch transiente thermische Berechnungen mit diesem Programm möglich.

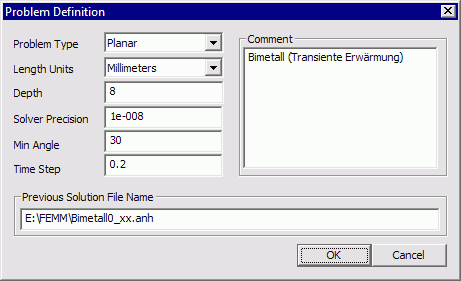
In dem Eingabefeld "Previous Solution File Name" kann man beschreiben, von welcher Lösung ausgehend der aktuelle Zeitschritt durchgeführt werden soll. Gibt man einen File-Namen an (.anh-Datei mit Ergebnissen der Wärmeberechnung), so wird das Eingabefeld für den "Time Step" aktiviert. Man kann dann angeben, wieviel Zeit von der vorherigen Lösung bis zur neu zu berechnenden Lösung vergehen soll:

• Auf dem Niveau der grafischen Oberfläche kann man damit nur extrem umständlich Schritt für Schritt durch den Zeitbereich bewegen!
• Praktikabel ist nur ein Script, welches diesen Prozess automatisiert.
• David Meeker hat ein Beispiel zur Verfügung gestellt. In diesem LUA-Script zeigt er, wie man sich ausgehend von einem Anfangszustand Schritt für Schritt durch eine Folge von Berechnungen bewegt, indem man den "Previous Solution File Name" ändert, während man in einer Schleife die gewünschte Zahl von Zeitschritten abarbeitet.

Mit diesem Wissen können wir die transiente Erwärmung unseres Bimetallstreifens ebenfalls auf Basis eines LUA-Scripts simulieren:

• Wir benutzen das mittels der grafischen Oberfläche bereits erstellte Modell Bimetall_xx.FEH.
• Das LUA-Script soll nur die Ablaufsteuerung im Zeitbereich übernehmen.

1. Berücksichtigung der Wärmekapazitäten

• Für die stationäre Berechnung des Endzustandes der Erwärmung waren die Werte für die spezifische Wärmekapazität der Materialien ohne Bedeutung, da sie im Gleichungssystem nicht benutzt wurden.
• Für die Materialien sind folgende massenbezogene Werte der spezifischen Wärmekapazität bekannt:
  • spez. Wärmekapazität (Kupfer) = 385 J/(kg·K)
  • spez. Wärmekapazität (Invar) = 514 J/(kg·K)
• Leider erwartet FEMM die Eingabe volumenbezogen in MJ/(m³·K). Wir müssen die Werte unter Berücksichtigung der Massedichten also erst umrechnen:
  • Massedichte (Kupfer) = 8960 kg/m³
  • Massedichte (Invar) = 8130 kg/m³
• Der volumenbezogene Wert in J/(m³·K) ergibt sich, indem man den massebezogenen Wert mit der Massedichte multipliziert. Die Umrechnung in MJ/(m³·K) ist dann einfach.
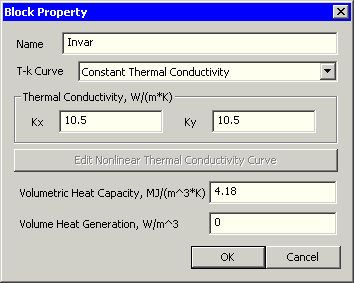
• Die Eintragung der korrekten Werte in die Material-Eigenschaften sollte man gründlich überprüfen:

2. Berechnung des Anfangszustandes für t=0 s

• Eigentlich kennen wir den Anfangszustand vor dem Einspeisen der Wärmeenergie in den Kupferstreifen. Der gesamte Bimetallstreifen besitzt die Umgebungstemperatur von 40°C.
• Mit diesem Zustand müssen wir jedoch eine Ergebnisdatei erzeugen, welche als Eingabedatei für den ersten Zeitschritt benötigt wird.
• Dazu erzeugen wir eine Kopie Bimetall0_xx.FEH unseres FEMM-Modells.
• In dieser Kopie setzen wir die Wärmeerzeugung im Kupfermaterial auf Null und führen eine normale stationäre Simulation durch. Infolge der automatischen Normierung der Farbskale wird das numerische Rauschen sichtbar:

• Es entsteht damit eine Ergebnisdatei Bimetall0_xx.anh, welche wir als Previous Solution File in der Problem-Definition für den ersten Zeitschritt der transienten Simulation nutzen können.

3. Verifizierung des transienten Modells für den ersten Zeitschritt

• Um unser stationäres Modell nicht zu zerstören, erzeugen wir daraus eine weitere Kopie Bimetall1_xx.FEH.
• Dieses Modell benutzen wir testweise zur Simulation des ersten Zeitschrittes von 0.2 s. Dazu müssen wir den kompletten Pfad für die zu verwendende Ergebnisdatei angeben:

• Nach 0.2 s hat sich der Kupferstreifen in der Mitte bereits um ca. 3 K erwärmt:

4. Ablaufsteuerung der transienten Simulation mittels LUA-Script

Wenn der transiente Simulationsprozess mit unserem Modell funktioniert, können wir mit dem Aufbau der Ablaufsteuerung mittels LUA-Script Bimetall_xx.LUA beginnen:

• Man kann für jeden Zeitschritt komfortabel die Ergebnisse der Modellrechnung mit den Funktionen des Postprozesses aufbereiten.
• Es gibt jedoch keine direkte Möglichkeit im FEMM, über die Zeitschritte hinweg den zeitlichen Verlauf von physikalischen Größen darzustellen.
• Um dies zu erreichen, muss man die benötigten Ergebnisse jedes Zeitschrittes in Dateien schreiben und nach der gesamten transienten Simulation mit separater Software diese Daten aufbereiten.
• Wir beschränken uns hier beispielhaft auf eine qualitative grafische Animation des zeitlichen Verlaufes der Erwärmung im Bimetall. Dazu erzeugen wir von jedem Zeitschritt eine Bitmap-Hardcopy des FEMM-Grafikfensters mit der als Farb-Kontur dargestellten Temperaturverteilung.
• Hinweis: Die Größe des Bitmap-Bildes ergibt sich aus der Größe des FEMM-Fensters beim Aufruf des LUA-Scripts.
• Die nicht mehr benötigten Modell- und Ergebnisdateien werden automatisch gelöscht, weil das nachträgliche manuelle Löschen sehr aufwändig ist.

-- aktuelle Teilnehmer-Nummer xx als Zeichenkette 00..99 verwenden!
-- myDir ist nicht erforderlich, da LUA-Script direkt im FEMM geöffnet wird
-- Zeitsteuerung
   Step  = 0.2; -- in [s]
   Steps = 100; -- entspricht 20s  
-- Berechnung der Knotentemperaturen für t=0 -> Ergebnisse in "Bimetall0_xx.anh"
   open("Bimetall0_xx.FEH");
   hi_analyze();
-- Hardcopy der aktuellen Temperaturverteilung als .BMP-Datei
   hi_loadsolution();
   hi_close();
-- ho_showdensityplot(legend,gscale,type,upper,lower)
   ho_showdensityplot(1,0,0,373.15,313.15,0);
   ho_savebitmap("Bimetall0_xx.bmp");
   ho_close();
-- Öffnen des transienten Modells    
   open("Bimetall1_xx.FEH");
   for n=1,Steps do
   -- Im aktuellen Modell wird 
   -- "Previous Solution File Name" auf die vorherige Ergebnisdatei gelenkt.
   -- "Time Step" auf Step gesetzt
   -- die übrigen Parameter müssen dem Modell des Anfangszustands entsprechen (gleiches Netz!):
      hi_probdef("millimeters","planar",1.e-8,8,30,"Bimetall"..(n-1).."_xx.anh",Step);
      hi_saveas("Bimetall"..n.."_xx.feh"); -- Speichern des modifizierten Modells
      hi_analyze();                        -- Berechnung mit dem aktuell gespeichertem Modell
   -- Hardcopy der aktuellen Temperaturverteilung als .BMP-Datei
      hi_loadsolution();                   	
   -- ho_showdensityplot(legend,gscale,type,upper,lower)
      ho_showdensityplot(1,0,0,373.15,313.15,0); -- Grenzen: 40°C-100°C
      ho_savebitmap("Bimetall"..n.."_xx.bmp");
   -- Löschen nicht mehr benötigter Dateien
      if n>1      then remove ("Bimetall"..n.."_xx.feh"); end;
      if n>1      then remove ("Bimetall"..(n-1).."_xx.anh"); end;
      if n==Steps then remove ("Bimetall"..(n).."_xx.anh"); end;
      ho_close();
   end;

Aus den Einzelbildern kann man nachträglich mit geeigneter Grafiksoftware z.B. eine animierte GIF-Datei erstellen, im Beispiel sieht man die Erwärmung ungefähr in Echtzeit:

← →