Software: FEM - Tutorial - 2D-Bauteil - Elastostatische FE-Simulation

↑

← →

Elastostatische Finite-Elemente-Simulation (Prinzip)

Nach über einhundert A4-Seiten Anleitung haben wir nun ein Gefühl dafür erhalten:

1. dass man mittels Finite-Elemente-Simulation die Belastung eines mechanischen Bauteils analysieren kann,
2. dafür unterschiedliche Software und Modell-Ansätze nutzbar sind und
3. dass der Aufwand für den gesamten Analyse-Prozess von relativ gering bis extrem hoch reicht.

Abschließend zu diesem Einstieg in den Prozess der FEM-Analyse sollen nun die physikalisch-mathematischen Grundlagen auf einem qualitativen Niveau verdeutlicht werden.

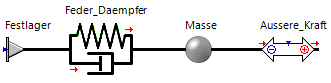
• Ausgangspunkt ist der reale Feder-Masse-Schwinger z.B. durch die Luft und die innere Reibung der Feder eine gewisse Dämpfung erfährt und den man durch eine äußere Kraft auf die schwingende Masse in seinem Verhalten beeinflussen kann:
  
• Das reale Objekt "Feder-Masse-Schwinger" kann man durch idealisierte Elemente mit konzentrierten Parametern (z.B. Punktmasse, Feder, Dämpfer, Einspannung, Kraftquelle) schematisch nachbilden:
  
• Anhand dieses Schemas ergibt sich die gewöhnliche Differentialgleichung des gedämpften Einmassen-Schwingers mit einem Freiheitsgrad der Bewegung:
  

m    Masse 
ü    Beschleunigung (a=dv/dt) 
c    Dämpfung 
ú    Geschwindigkeit (v=du/dt) 
k    Steifigkeit 
u    Verschiebung (Auslenkung) 
f(t) zeitlich veränderliche Kraft 

Die Terme der Gleichung beschreiben 3 Kraftwirkungen, deren Summe mit der Erregung (der Last) im Gleichgewicht steht:

F_m= m·ü  Trägheitskraft infolge Beschleunigung

F_c = c·ú   Dämpfungskraft infolge Geschwindigkeit

F_k = k·u   Rückstellkraft infolge Auslenkung

Diese Reduktion auf "konzentrierte Elemente" gelingt gut, wenn die Bauteile selbst als Funktionselemente im Sinne dieser "konzentrierten Elemente" benutzt werden (z.B. Gewindefedern, Stoßdämpfer, Massestücke). Innerhalb dieser "konzentrierten Elemente" kann man damit im Normalfall nur eine homogene Belastung berechnen.

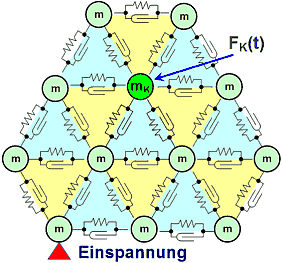
Im Unterschied dazu wird bei der Finite-Elemente-Methode das Innere von mechanischen Bauteilen in extrem viele Massepunkte (Knoten) diskretisiert, welche wechselwirkend über die Steifigkeit und Dämpfung des dazwischenliegenden Materials (Elemente) verbunden sind. Es ergibt sich daraus die folgende Ersatzschaltung (Beispiel-Netz aus Dreieck-Elementen):

Jeder Knoten beschreibt einen Massepunkt:

• Aus der Massedichte der Materialien und der Geometrie der Elemente ist die Masse eines jedes Elementes bestimmbar.
• Diese Elementmasse wird so auf die Knoten des Elements verteilt, dass für jedes Element die Summe aller Knotenmassen gleich der Elementmasse ist und die Teilmassen den gleichen gemeinsamen Schwerpunkt besitzen wie das Element.
• Werden Knoten von mehreren Elementen benutzt (der Normalfall), so ergibt sich ihre Masse als Summe aller anteiligen Elementmassen.
• Jeder Knoten ist über Feder-Dämpfer mit allen seinen Nachbarn verbunden (Bei QUAD-Elementen verlaufen z.B. auch über die Viereck-Diagonalen Feder-Dämpfer).
• Kraftvektoren (Lastvektoren) greifen direkt an den einzelnen Knoten an und widerspiegeln den Einfluss der Netzumgebung (angedeutet mit F_K(t) an Knoten m_K).

Die Finite-Elemente-Methode basiert in der Domäne der Mechanik auf dieser Bewegungsgleichung. Sie wird jedoch verallgemeinert zum allgemeinen Mehrmassenschwinger als Matrizen-Gleichung ausgeführt:

{M}    Massenmatrix 
{ü}    Beschleunigungsvektor 
{C}    Dämpfungsmatrix 
{ú}    Geschwindigkeitsvektor 
{K}    Steifigkeitsmatrix 
{u}    Verschiebungsvektor 
{F(t)} Kraftvektor (Lastvektor) 

Die Größe der Matrizen und Vektoren wird durch die Anzahl der Knoten des Netzes bestimmt. Dem Gleichungssystem entspricht die obige Ersatzschaltung.

1. Primär-Ergebnisse der FEM-Berechnung für jeden Knoten

• Vektorgrößen mit den max. 6 Freiheitsgraden der Bewegung

2. Sekundär-Ergebnisse der FEM-Berechnung

• Vektorgrößen der Haupt- und Vergleichsspannungen sowie der Lagerkräfte

3. Energieformen

• Potentielle und kinetische Energie (ermöglicht Oszillation)

4. Max. Anzahl der zeitlichen Ableitungen der Primär-Ergebnisse

• bis zur 2.Ableitung (Weg, Geschwindigkeit, Beschleunigung)

Mit den vollständigen Gleichungen für die mechanische bzw. thermische Domäne ist eine Simulation der wechselwirkenden Zustandsänderung jedes Knoten im Zeitbereich möglich (=dynamischer Modellansatz). Aus Gründen des Berechnungsaufwandes begnügt man sich meist mit Stationärer (statischer) Berechnung, deren Vereinfachungen im Folgenden beschrieben werden:

• Modellansatz ohne Speicher-Elemente (Massen).
• Elemente, die nur bei zeitlichen Änderungen der Primär-Ergebnisse wirksam sind, werden nicht berücksichtigt (z.B. Dämpfer in der Mechanik).
• Die Last auf das Netz ist konstant.
• Berechnet wird der Endzustand (eingeschwungener Zustand) nach Aufbringen der Last (Stationärer Zustand).
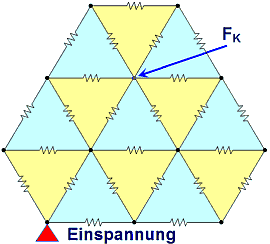
• Die Ersatzschaltung reduziert sich für die Strukturmechanik auf ein Netz von Steifigkeiten. Zwischen dem Knoten mit der angedeuteten Krafteinleitung und dem eingespannten Knoten ergibt sich dabei eine Ersatzsteifigkeit. Dies gilt prinzipiell auch bei mehreren belasteten bzw. gelagerten Knoten:
  

===>>> Die Seite wird zur Zeit erstellt !!!

← →