Software: SimX - Nadelantrieb - Wirkprinzip - Guetefunktion: Unterschied zwischen den Versionen
K (Änderungen von Alfred Kamusella (Beiträge) rückgängig gemacht und letzte Version von Steve Krueger wiederhergestellt) |
|||
| Zeile 1: | Zeile 1: | ||
[[Software:_SimX_-_Nadelantrieb_-_Wirkprinzip|↑]] <div align="center"> [[Software:_SimX_-_Nadelantrieb_-_Wirkprinzip_-_Federvorspannung|←]] [[Software:_SimX_-_Nadelantrieb_-_Wirkprinzip_-_Zielfunktion|→]] </div><div align="center">[[Bild:Software_SimX_-_Nadelantrieb_-_Wirkprinzip_-_3d-kurve_tzyklus_titel.gif| ]]</div> | [[Software:_SimX_-_Nadelantrieb_-_Wirkprinzip|↑]] <div align="center"> [[Software:_SimX_-_Nadelantrieb_-_Wirkprinzip_-_Federvorspannung|←]] [[Software:_SimX_-_Nadelantrieb_-_Wirkprinzip_-_Zielfunktion|→]] </div><div align="center">[[Bild:Software_SimX_-_Nadelantrieb_-_Wirkprinzip_-_3d-kurve_tzyklus_titel.gif| ]]</div> | ||
<div align="center">'''Experiment: 3D-Gütefunktion (Rastersuche)''' </div> | <div align="center">'''Experiment: 3D-Gütefunktion (Rastersuche)''' </div> | ||
'''''Achtung:''' Die folgenden Abschnitte wurden noch nicht im Sinne der neuen Modellstruktur überarbeitet. Das prinzipielle Vorgehen bleibt jedoch weiterhin gültig!'' | |||
| Zeile 9: | Zeile 12: | ||
Die Gütefunktion wird in unserem Beispiel nur durch das Gütekriterium ''tZyklus'' gebildet. Während der Optimierung wird als Nennwert-Verlauf praktisch ein Höhenprofil des auf der Oberfläche der Gütefunktion zurückgelegten Pfades abgebildet:<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Wirkprinzip_-_hoehenprofil_suchpfad.gif| ]] </div> | Die Gütefunktion wird in unserem Beispiel nur durch das Gütekriterium ''tZyklus'' gebildet. Während der Optimierung wird als Nennwert-Verlauf praktisch ein Höhenprofil des auf der Oberfläche der Gütefunktion zurückgelegten Pfades abgebildet:<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Wirkprinzip_-_hoehenprofil_suchpfad.gif| ]] </div> | ||
Der Wert der Zykluszeit ist bisher eine Funktion von den vier Entwurfsparametern: | Der Wert der Zykluszeit ist bisher eine Funktion von den vier Entwurfsparametern: | ||
| Zeile 24: | Zeile 21: | ||
Das Optimierungsproblem soll deshalb auf zwei Entwurfsparameter zurückgeführt werden. Wir erhalten dann bei hinreichend feiner Abtastung | Das Optimierungsproblem soll deshalb auf zwei Entwurfsparameter zurückgeführt werden. Wir erhalten dann bei hinreichend feiner Abtastung der Gütefunktion eine anschauliche 3D-Fläche. Dazu sind im Folgenden einige Änderungen am Simulationsmodell erforderlich: | ||
* Wir führen eine Simulation mit dem unter Vorspannung der Rückholfeder erreichten Bestwert durch ('''Analyse - Bestwert - Simulation durchführen'''). Danach besitzt das SimulationX-Modell die Parameter dieser optimalen Lösung. | |||
* Im SimulationX speichern wir die Modell-Datei mit diesen Parametern, weil wir bei der Modelländerung auf diese Optimal-Lösung Bezug nehmen werden. | |||
* Wir beeenden das OptiY. Damit wird auch das Modell in SimulationX geschlossen. Damit vermeiden wir nach der erforderlichen Modelländerung Probleme beim Datenaustausch zwischen OptiY und SimulationX. | |||
* Für die Modelländerung öffnen wir erneut im SimulationX das optimal konfigurierte Modell. | |||
<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Wirkprinzip_-_optimum_abschaltung.gif| ]] </div> | |||
Die Modelländerung basiert auf folgenden Üerlegungen: | |||
*'''Nadel_x0=0.15 mm''' | *'''Nadel_x0=0.15 mm''' | ||
:Die bisherigen Experimente zeigten, dass es am günstigsten ist, die Nadelspitze in der Ruhelage direkt auf der Papieroberfläche zu platzieren. Der Wert dieses Entwurfsparameters kann also konstant auf diesen Wert gesetzt werden! Wir setzen im SimulationX-Modell ''Nadel.x0=0.15 mm''. | :Die bisherigen Experimente zeigten, dass es am günstigsten ist, die Nadelspitze in der Ruhelage direkt auf der Papieroberfläche zu platzieren. Der Wert dieses Entwurfsparameters kann also konstant auf diesen Wert gesetzt werden! Wir setzen im SimulationX-Modell ''Nadel.x0=0.15 mm'', was durch Übernahme des Bestwertes wahrscheinlich schon erfolgt war. | ||
*'''Magnet_R - Abschaltung, wenn | *'''Magnet_R - Abschaltung, wenn Papier-Riss''' | ||
:Die Einschaltdauer der Magnetkraft muss vom Optimierungsverfahren kontinuierlich an die aktuelle Konfiguration von Ankerdurchmesser, Nadel-Ruhelage und Rückholfeder angepasst werden. Nur so kann für die aktuelle mechanische Konfiguration ein möglichst schnelles und sicheres Prägen des Papiers erreicht werden. | :Die Einschaltdauer der Magnetkraft muss vom Optimierungsverfahren kontinuierlich an die aktuelle Konfiguration von Ankerdurchmesser, Nadel-Ruhelage und Rückholfeder angepasst werden. Nur so kann für die aktuelle mechanische Konfiguration ein möglichst schnelles und sicheres Prägen des Papiers erreicht werden. | ||
:Diese Anpassung der Einschaltzeit kann man durch eine Änderung des Simulationsmodells automatisieren, indem man die Magnetkraft in Abhängigkeit | : Anhand der optimalen Lösung erkennt man, dass die Abschaltung ziemlich exakt beim Riss des Papiers erfolgt. Die kinetische Energie der bewegten Masse ist dann ausreichend, um den Prägevorgang zu vollenden. | ||
:Diese Anpassung der Einschaltzeit kann man durch eine Änderung des Simulationsmodells automatisieren, indem man die Magnetkraft in Abhängigkeit von der Nadelposition beeinflusst. | |||
*'''tZyklus=f(d_Anker, Feder_k)''' | *'''tZyklus=f(d_Anker, Feder_k)''' | ||
:Die | :Die reduzierte 3D-Gütefunktion wird wahrscheinlich das globale Optimum enthalten. Die Reduzierung der Dimensionen wird durch Berücksichtigung bekannter Abhängigkeiten im Simulationsmodell bzw. in der Experiment-Konfiguration erreicht. | ||
| Zeile 39: | Zeile 43: | ||
Das für die Abschaltung benötigte Status-Signal steht uns mit ''''' | Das für die Abschaltung benötigte Status-Signal steht uns mit '''''Riss.y''''' im Modell bereits zur Verfügung. | ||
Problematischer ist die Ermittlung eines hinreichend genauen Wertes für '''''Fmax''''', hier sind einige Tricks erforderlich: | Problematischer ist die Ermittlung eines hinreichend genauen Wertes für '''''Fmax''''', hier sind einige Tricks erforderlich: | ||
* ''Fmax'' wurde bisher als Amplitude eines Sägezahn-Dreiecks vorgegebener Länge berechnet. | * ''Fmax'' wurde bisher als Amplitude eines Sägezahn-Dreiecks vorgegebener Länge berechnet. | ||
* Die Kraft soll nun automatisch abgeschaltet werden, wenn das Papier | * Die Kraft soll nun automatisch abgeschaltet werden, wenn das Papier am Prägepunkt reißt: Riss.y=t(xRiss). | ||
* Da bei dieser automatischen Abschaltung der Abschaltzeitpunkt vorher unbekannt ist, kann der Dreiecksimpuls nicht mehr genutzt werden (Endwert von Fmax kann nicht realisiert werden!). | * Da bei dieser automatischen Abschaltung der Abschaltzeitpunkt vorher unbekannt ist, kann der Dreiecksimpuls nicht mehr genutzt werden (Endwert von Fmax kann nicht realisiert werden!). | ||
* Deshalb wollen wir den Verlauf F=f(x) für die optimal angepasste Einschaltdauer näherungsweise nachbilden: | * Deshalb wollen wir den Verlauf F=f(x) für die optimal angepasste Einschaltdauer näherungsweise nachbilden: | ||
** Der optimale Zeitpunkt für die Kraftabschaltung ist | ** Der optimale Zeitpunkt für die Kraftabschaltung ist nahe der Rissposition ''x=-0.39 mm''.<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Wirkprinzip_-_fmag_von_x_dreieck.gif| ]] </div>Die Nadel fliegt dann auf Grund ihrer Masseträgheit noch bis zum Anschlag und prägt das Papier komplett. | ||
** Die Form der Funktion Fmagn=f(x) entspricht weitestgehend einer quadratischen Funktion mit dem Wert ''Fmax'' zum Abschaltzeitpunkt. Das kann man bei Vernachlässigung der nichtlinearen Papierkräfte für dieses einfache Feder-Masse-System auch analytisch nachvollziehen. | ** Die Form der Funktion Fmagn=f(x) entspricht weitestgehend einer quadratischen Funktion mit dem Wert ''Fmax'' zum Abschaltzeitpunkt. Das kann man bei Vernachlässigung der nichtlinearen Papierkräfte für dieses einfache Feder-Masse-System auch analytisch nachvollziehen. | ||
** Man muss dabei beachten, dass sich die Nadel erst bewegen kann, wenn die Vorspannkraft der Feder überwunden wird. Die Vorspannkraft von ca. 1 N ist im Vergleich zu ca. Fmax=50 N relativ gering (bei einer Masse von 10 g und einer Beschleunigung von 10 g). | ** Man muss dabei beachten, dass sich die Nadel erst bewegen kann, wenn die Vorspannkraft der Feder überwunden wird. Die Vorspannkraft von ca. 1 N ist im Vergleich zu ca. Fmax=50 N relativ gering (bei einer Masse von 10 g und einer Beschleunigung von 10 g). | ||
** Die Größe | ** Die Größe Praegung.y ändert sich beim Vorschub der Nadel von 0 auf 1. Dies soll genutzt werden, um den erforderlichen quadratischen Verlauf von ''Luftspalt.F'' näherungsweise nachzubilden. Die Anfangskraft für die Überwindung der Vorspannung wurde auf Fmax/10 gesetzt:<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Wirkprinzip_-_fmag_von_x_ersatz.gif| ]] </div>Die kräftig blaue Kurve im obigen Bild entspricht der folgenden Formel, welche im Parameterfeld des Luftspalt-Elements eingetragen wurde. Der Ausdruck <tt>'''1-sign(Riss.y)'''</tt> springt von Eins auf Null, wenn die Rissposition erreicht wird: | ||
Geometrie.Fmax*(0.1+ | Geometrie.Fmax*(0.1+sqrt(Praegung.y))*(1-sign(Riss.y)) | ||
* Im Vergleich dazu sieht man etwas blasser die eingefrorenen Signale, welche der Ansteuerung mit einem Dreiecksimpuls der Kraft entsprechen. | |||
* Das Verhalten des Magnet-Antriebs unterscheidet sich mit diesem Kraftansatz fast nicht vom optimal eingestellten bisherigen Dreiecksverlauf Fmagn=f(t). | * Das Verhalten des Magnet-Antriebs unterscheidet sich mit diesem Kraftansatz fast nicht vom optimal eingestellten bisherigen Dreiecksverlauf Fmagn=f(t):<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Wirkprinzip_-_optimum_autoabschalt.gif| ]] </div> | ||
* Der Element-Typ ''MagnGeo'' soll nun so modifiziert werden, dass in Abhängigkeit von einem REAL-Parameter '''''Abschaltung'''''(0=Dreieck / 1=Auto) eine angepasste Berechnung von Fmax erfolgt: | * Der Element-Typ ''MagnGeo'' soll nun so modifiziert werden, dass in Abhängigkeit von einem REAL-Parameter '''''Abschaltung''''' (0=Dreieck / 1=Auto) eine angepasste Berechnung von ''Fmax'' erfolgt: | ||
** Wir ergänzen in ''MagnGeo'' den Parameter ''Abschaltung'' mit entsprechendem Kommentar. | ** Wir ergänzen in ''MagnGeo'' den Parameter ''Abschaltung'' mit entsprechendem Kommentar. | ||
** Den Impulsgenerator ''Magnet'' verändern wir nicht. Er wird also weiterhin nur Dreiecksimpulse mit der vorgegebenen Amplitude ''Fmax'' erzeugen. | ** Den Impulsgenerator ''Magnet'' verändern wir nicht. Er wird also weiterhin nur Dreiecksimpulse mit der vorgegebenen Amplitude ''Fmax'' erzeugen. | ||
** Die Umschaltung zwischen Dreiecksimpuls und Rechteckverlauf soll im Element ''Luftspalt'' für den Parameter ''F'' erfolgen. Der erste Summand entspricht dem eingespeisten Dreiecksimpuls, der zweite Summand der Ersatzfunktion. In Abhängigkeit des Wertes von ''Geometrie.Abschaltung'' (0,1) wirkt nur einer der beiden Summanden: | ** Die Umschaltung zwischen Dreiecksimpuls und Rechteckverlauf soll im Element ''Luftspalt'' für den Parameter ''F'' erfolgen. Der erste Summand entspricht dem eingespeisten Dreiecksimpuls, der zweite Summand der Ersatzfunktion. In Abhängigkeit des Wertes von ''Geometrie.Abschaltung'' (0,1) wirkt nur einer der beiden Summanden: | ||
self.in1*(1-Geometrie.Abschaltung) + Geometrie.Fmax*(0.1+ | self.in1*(1-Geometrie.Abschaltung) + Geometrie.Fmax*(0.1+sqrt(Preagung.y))*(1-sign(Riss.y))*Geometrie.Abschaltung | ||
* Die sichere Funktion beider Betriebsmodi sollte man unbedingt überprüfen! | * Die sichere Funktion beider Betriebsmodi sollte man unbedingt überprüfen! | ||
* '''Achtung:''' Um Probleme mit unserem bereits konfigurierten OptiY-Experiment zu vermeiden, setzen wir '''''Abschaltung=0'''''. Damit ist standardmäßig der bisherige Betriebsmodus mit Impulsgenerator wirksam. | * '''Achtung:''' Um Probleme mit unserem bereits konfigurierten OptiY-Experiment zu vermeiden, setzen wir vor dem Speichern des Modells '''''Abschaltung=0'''''. Damit ist standardmäßig der bisherige Betriebsmodus mit Impulsgenerator wirksam. | ||
== Konfiguration eines neuen OptiY-Experiments == | == Konfiguration eines neuen OptiY-Experiments == | ||
| Zeile 87: | Zeile 91: | ||
* Im Sinne einer effektiven Nutzung der knappen Übungszeit werden hier günstige Grenzwerte vorgegeben: | * Im Sinne einer effektiven Nutzung der knappen Übungszeit werden hier günstige Grenzwerte vorgegeben: | ||
** '''d_Anker = 8...16 mm''' | ** '''d_Anker = 8...16 mm''' | ||
** '''Feder_k = 8... | ** '''Feder_k = 8...200 N/mm''' | ||
* Als Optimierungsverfahren wählen wir die Rastersuche mit | * Als Optimierungsverfahren wählen wir die Rastersuche mit 900 Abtastschritten:<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Wirkprinzip_-_3d-kurve_rastersuche_konfig.gif| ]] </div> | ||
** Der Bereich jedes Entwurfsparameters wird dabei in gleichmäßigen Abständen an | ** Der Bereich jedes Entwurfsparameters wird dabei in gleichmäßigen Abständen an 30 Punkten abgetastet. | ||
** | ** 30x30=900 Simulationsläufe sind ein günstiger Kompromiss zwischen Rechenzeit und Feinheit der Abtastung. Auf "betagter" Hardware genügen zur Not auch eine Rasterung von 20x20=400. | ||
** Der Rechenzeitbedarf steigt quadratisch mit der Feinheit der Rasterung! | ** Der Rechenzeitbedarf steigt quadratisch mit der Feinheit der Rasterung! | ||
'''''Hinweis:''''' | |||
In der Simulationssteuerung von SimulationX '''tStop''' muss größer gewählt werden, als der längste Prägezyklus im Suchraum! Im Beispiel sollte tStop=10 ms ausreichen. | |||
* Das 3D-Diagramm für das Gütekriterium ''tZyklus=f(d_Anker, Feder_k)'' kann man bereits vor dem Start der Optimierung öffnen ('''Analyse - Darstellung - 3D-Darstellung'''). | * Das 3D-Diagramm für das Gütekriterium ''tZyklus=f(d_Anker, Feder_k)'' kann man bereits vor dem Start der Optimierung öffnen ('''Analyse - Darstellung - 3D-Darstellung'''). | ||
*[[Bild:Software_SimX_-_Nadelantrieb_-_Wirkprinzip_-_3d-kurve_konfig_3d.gif|right]] Nach Start der Optimierung baut sich Stück für Stück die 3D-Fläche im Diagramm auf. | *[[Bild:Software_SimX_-_Nadelantrieb_-_Wirkprinzip_-_3d-kurve_konfig_3d.gif|right]] Nach Start der Optimierung baut sich Stück für Stück die 3D-Fläche im Diagramm auf. | ||
** Ein Mausklick auf das 3D-Diagramm ermöglicht im Eigenschaftsfeld die Konfiguration der Darstellung. Mit dem Einschalten aller Optionen erhält man eine gute Flächendarstellung und erkennt die einzelnen Schritte anhand der Punkte. | ** Ein Mausklick auf das 3D-Diagramm ermöglicht im Eigenschaftsfeld die Konfiguration der Darstellung. Mit dem Einschalten aller Optionen erhält man eine gute Flächendarstellung und erkennt die einzelnen Schritte anhand der Punkte. | ||
** Mit dem Maus-Cursor lässt sich die Darstellung drehen, so dass man sich günstige Ansichten einstellen kann:<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Wirkprinzip_-_3d- | ** Mit dem Maus-Cursor lässt sich die Darstellung drehen, so dass man sich günstige Ansichten einstellen kann: | ||
<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Wirkprinzip_-_3d-kurve_tzyklus_stabil.gif| ]] </div> | |||
'''Interpretation der Gütefunktion''' | '''Interpretation der Gütefunktion''' | ||
* Die Magnetkraft schaltet nach Erreichen der Riss-Position ab: | |||
** Reicht die Kraft nicht aus, diese Rissposition zu erreichen, so kehrt die Nadel nicht mehr in die Ruhelage zurück, weil die Kraft nicht abschaltet. | |||
* Die Magnetkraft schaltet | |||
** Reicht die Kraft | |||
** In diesem Fall wird auf Grund des Messprinzips ''tZyklus=0 s'' ermittelt, obwohl praktisch ''tZyklus=unendlich'' ist! | ** In diesem Fall wird auf Grund des Messprinzips ''tZyklus=0 s'' ermittelt, obwohl praktisch ''tZyklus=unendlich'' ist! | ||
* Die Z-Achse (tZyklus) des 3D-Diagramms wird automatisch zwischen Minimalwert (0 s) und Maximalwert (langsamster Prägezyklus) skaliert: | * Die Z-Achse (tZyklus) des 3D-Diagramms wird automatisch zwischen Minimalwert (0 s) und Maximalwert (langsamster Prägezyklus) skaliert: | ||
| Zeile 116: | Zeile 118: | ||
** Die "Zacken" an der Grenze des zulässigen Lösungsbereichs resultieren aus dem Abtast-Raster. | ** Die "Zacken" an der Grenze des zulässigen Lösungsbereichs resultieren aus dem Abtast-Raster. | ||
* Um die abgebildete Gütefunktion mehr den "natürlichen" Gegebenheiten anzupassen und gleichzeitig eine bessere Skalierung in Z-Richtung zu erhalten, genügt eine einfache Änderung: | * Um die abgebildete Gütefunktion mehr den "natürlichen" Gegebenheiten anzupassen und gleichzeitig eine bessere Skalierung in Z-Richtung zu erhalten, genügt eine einfache Änderung: | ||
** Wir setzen für den Anfangswert '''tZyklus.y0=0.0034''' unter den globalen Modellparametern. | ** Wir setzen für den Anfangswert '''tZyklus.y0=0.0034''' unter den globalen Modellparametern. Damit erscheint dieser Wert von 3,4 ms beim Nichtprägen. | ||
** Man erkennt dann im Bild, dass für diesen Zustand die Zykluszeit steil ansteigt (praktisch gegen Unendlich geht). | ** Man erkennt dann im Bild, dass für diesen Zustand die Zykluszeit steil ansteigt (praktisch gegen Unendlich geht). | ||
** Dieses Plateau markiert gleichzeitig die Forderung für die maximal zulässige Zykluszeit. | ** Dieses Plateau markiert gleichzeitig die Forderung für die maximal zulässige Zykluszeit. | ||
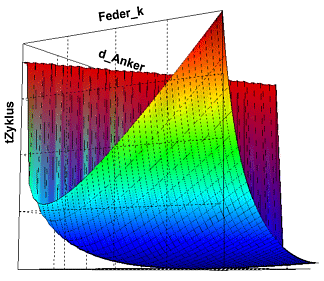
** Nach | ** Nach Rücksetzen und erneutem Start der Rastersuche erhalten wir eine günstigere Darstellung Gütefunktion ''tZyklus=f(d_Anker, Feder_k)'':<div align="center">[[Bild:Software_SimX_-_Nadelantrieb_-_Wirkprinzip_-_3d-kurve_tzyklus_grenzwert.gif| ]]</div> | ||
Das globale Optimum liegt in einer flachen Mulde unweit der Grenze zum "Nichtprägen", | Das globale Optimum liegt in einer flachen Mulde unweit der Grenze zum "Nichtprägen". Etwas darüber existiert, getrennt durch einen Wall eine weitere flache Mulde mit einem lokalem Minimum. Daraus kann man folgende Schlussfolgerungen ziehen: | ||
# In Abhängigkeit vom gewählten Startpunkt (=Anfangslösung) findet ein lokales Optimierungsverfahren eines der beiden Optima, wovon aber nur eines das globale Optimum darstellt. | |||
# Insbesondere die Federkonstante kann in einem weiten Bereich verändert werden, ohne dass sich die Zykluszeit in relevanten Größenordnungen ändert. Man kann sich bei der Wahl eines konkreten Wertes an der technischen Realisierbarkeit orientieren. | # Insbesondere die Federkonstante kann in einem weiten Bereich verändert werden, ohne dass sich die Zykluszeit in relevanten Größenordnungen ändert. Man kann sich bei der Wahl eines konkreten Wertes an der technischen Realisierbarkeit orientieren. | ||
# Zur gewählten Federsteife kann man einen geeigneten Ankerdurchmesser wählen, der einen hinreichend schnellen Prägezyklus ermöglicht. | # Zur gewählten Federsteife kann man einen geeigneten Ankerdurchmesser wählen, der einen hinreichend schnellen Prägezyklus ermöglicht. | ||
Version vom 14. August 2009, 13:38 Uhr
Achtung: Die folgenden Abschnitte wurden noch nicht im Sinne der neuen Modellstruktur überarbeitet. Das prinzipielle Vorgehen bleibt jedoch weiterhin gültig!
Das Hooke-Jeeves-Verfahren konvergiert durch ständige Abwärtsbewegung auf der Gütefunktion zum nächstgelegenen Minimum:
- Es handelt sich zumindest um ein lokales Minimum auf der Gütefunktion.
- Man kann sich dabei jedoch nie sicher sein, ob nicht doch noch Kombinationen für die Entwurfsparameter existieren, welche zu einer besseren Lösung führen (möglichst zum globalen Minimum der Gütefunktion).
- Es wäre günstig, wenn man die Topografie der Gütefunktion in Analogie zu einer Landkarte kennen würde. Für unser Optimierungsproblem wollen wir dies in vereinfachter Form versuchen zu realisieren.
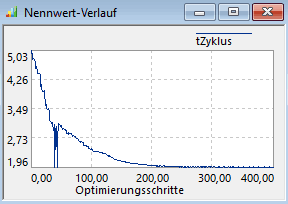
Die Gütefunktion wird in unserem Beispiel nur durch das Gütekriterium tZyklus gebildet. Während der Optimierung wird als Nennwert-Verlauf praktisch ein Höhenprofil des auf der Oberfläche der Gütefunktion zurückgelegten Pfades abgebildet:
Der Wert der Zykluszeit ist bisher eine Funktion von den vier Entwurfsparametern:
- d_Anker
- Feder_k
- Magnet_R
- Nadel_x0
Geometrisch handelt es sich bei der kompletten Gütefunktion also um eine 5D-Hyperfläche, welche für uns 3½D-Lebewesen schwer vorstellbar ist.
Das Optimierungsproblem soll deshalb auf zwei Entwurfsparameter zurückgeführt werden. Wir erhalten dann bei hinreichend feiner Abtastung der Gütefunktion eine anschauliche 3D-Fläche. Dazu sind im Folgenden einige Änderungen am Simulationsmodell erforderlich:
- Wir führen eine Simulation mit dem unter Vorspannung der Rückholfeder erreichten Bestwert durch (Analyse - Bestwert - Simulation durchführen). Danach besitzt das SimulationX-Modell die Parameter dieser optimalen Lösung.
- Im SimulationX speichern wir die Modell-Datei mit diesen Parametern, weil wir bei der Modelländerung auf diese Optimal-Lösung Bezug nehmen werden.
- Wir beeenden das OptiY. Damit wird auch das Modell in SimulationX geschlossen. Damit vermeiden wir nach der erforderlichen Modelländerung Probleme beim Datenaustausch zwischen OptiY und SimulationX.
- Für die Modelländerung öffnen wir erneut im SimulationX das optimal konfigurierte Modell.
Die Modelländerung basiert auf folgenden Üerlegungen:
- Nadel_x0=0.15 mm
- Die bisherigen Experimente zeigten, dass es am günstigsten ist, die Nadelspitze in der Ruhelage direkt auf der Papieroberfläche zu platzieren. Der Wert dieses Entwurfsparameters kann also konstant auf diesen Wert gesetzt werden! Wir setzen im SimulationX-Modell Nadel.x0=0.15 mm, was durch Übernahme des Bestwertes wahrscheinlich schon erfolgt war.
- Magnet_R - Abschaltung, wenn Papier-Riss
- Die Einschaltdauer der Magnetkraft muss vom Optimierungsverfahren kontinuierlich an die aktuelle Konfiguration von Ankerdurchmesser, Nadel-Ruhelage und Rückholfeder angepasst werden. Nur so kann für die aktuelle mechanische Konfiguration ein möglichst schnelles und sicheres Prägen des Papiers erreicht werden.
- Anhand der optimalen Lösung erkennt man, dass die Abschaltung ziemlich exakt beim Riss des Papiers erfolgt. Die kinetische Energie der bewegten Masse ist dann ausreichend, um den Prägevorgang zu vollenden.
- Diese Anpassung der Einschaltzeit kann man durch eine Änderung des Simulationsmodells automatisieren, indem man die Magnetkraft in Abhängigkeit von der Nadelposition beeinflusst.
- tZyklus=f(d_Anker, Feder_k)
- Die reduzierte 3D-Gütefunktion wird wahrscheinlich das globale Optimum enthalten. Die Reduzierung der Dimensionen wird durch Berücksichtigung bekannter Abhängigkeiten im Simulationsmodell bzw. in der Experiment-Konfiguration erreicht.
Automatische Abschaltung der Magnetkraft
Das für die Abschaltung benötigte Status-Signal steht uns mit Riss.y im Modell bereits zur Verfügung. Problematischer ist die Ermittlung eines hinreichend genauen Wertes für Fmax, hier sind einige Tricks erforderlich:
- Fmax wurde bisher als Amplitude eines Sägezahn-Dreiecks vorgegebener Länge berechnet.
- Die Kraft soll nun automatisch abgeschaltet werden, wenn das Papier am Prägepunkt reißt: Riss.y=t(xRiss).
- Da bei dieser automatischen Abschaltung der Abschaltzeitpunkt vorher unbekannt ist, kann der Dreiecksimpuls nicht mehr genutzt werden (Endwert von Fmax kann nicht realisiert werden!).
- Deshalb wollen wir den Verlauf F=f(x) für die optimal angepasste Einschaltdauer näherungsweise nachbilden:
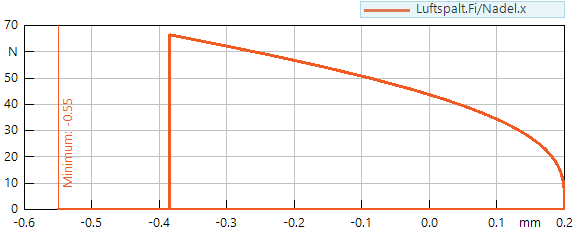
- Der optimale Zeitpunkt für die Kraftabschaltung ist nahe der Rissposition x=-0.39 mm.Die Nadel fliegt dann auf Grund ihrer Masseträgheit noch bis zum Anschlag und prägt das Papier komplett.
- Die Form der Funktion Fmagn=f(x) entspricht weitestgehend einer quadratischen Funktion mit dem Wert Fmax zum Abschaltzeitpunkt. Das kann man bei Vernachlässigung der nichtlinearen Papierkräfte für dieses einfache Feder-Masse-System auch analytisch nachvollziehen.
- Man muss dabei beachten, dass sich die Nadel erst bewegen kann, wenn die Vorspannkraft der Feder überwunden wird. Die Vorspannkraft von ca. 1 N ist im Vergleich zu ca. Fmax=50 N relativ gering (bei einer Masse von 10 g und einer Beschleunigung von 10 g).
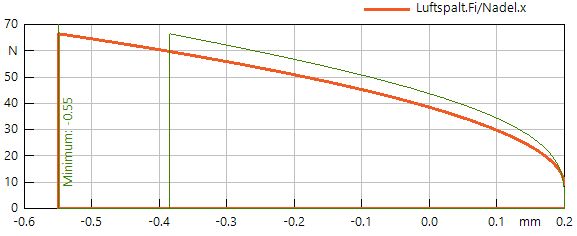
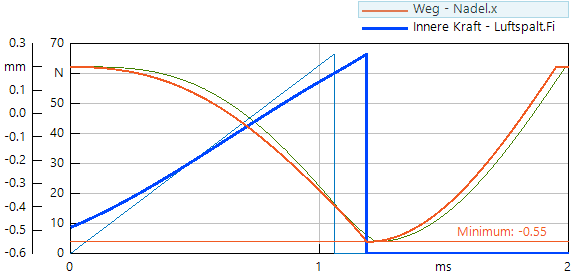
- Die Größe Praegung.y ändert sich beim Vorschub der Nadel von 0 auf 1. Dies soll genutzt werden, um den erforderlichen quadratischen Verlauf von Luftspalt.F näherungsweise nachzubilden. Die Anfangskraft für die Überwindung der Vorspannung wurde auf Fmax/10 gesetzt:Die kräftig blaue Kurve im obigen Bild entspricht der folgenden Formel, welche im Parameterfeld des Luftspalt-Elements eingetragen wurde. Der Ausdruck 1-sign(Riss.y) springt von Eins auf Null, wenn die Rissposition erreicht wird:
Geometrie.Fmax*(0.1+sqrt(Praegung.y))*(1-sign(Riss.y))
- Im Vergleich dazu sieht man etwas blasser die eingefrorenen Signale, welche der Ansteuerung mit einem Dreiecksimpuls der Kraft entsprechen.
- Das Verhalten des Magnet-Antriebs unterscheidet sich mit diesem Kraftansatz fast nicht vom optimal eingestellten bisherigen Dreiecksverlauf Fmagn=f(t):
- Der Element-Typ MagnGeo soll nun so modifiziert werden, dass in Abhängigkeit von einem REAL-Parameter Abschaltung (0=Dreieck / 1=Auto) eine angepasste Berechnung von Fmax erfolgt:
- Wir ergänzen in MagnGeo den Parameter Abschaltung mit entsprechendem Kommentar.
- Den Impulsgenerator Magnet verändern wir nicht. Er wird also weiterhin nur Dreiecksimpulse mit der vorgegebenen Amplitude Fmax erzeugen.
- Die Umschaltung zwischen Dreiecksimpuls und Rechteckverlauf soll im Element Luftspalt für den Parameter F erfolgen. Der erste Summand entspricht dem eingespeisten Dreiecksimpuls, der zweite Summand der Ersatzfunktion. In Abhängigkeit des Wertes von Geometrie.Abschaltung (0,1) wirkt nur einer der beiden Summanden:
self.in1*(1-Geometrie.Abschaltung) + Geometrie.Fmax*(0.1+sqrt(Preagung.y))*(1-sign(Riss.y))*Geometrie.Abschaltung
- Die sichere Funktion beider Betriebsmodi sollte man unbedingt überprüfen!
- Achtung: Um Probleme mit unserem bereits konfigurierten OptiY-Experiment zu vermeiden, setzen wir vor dem Speichern des Modells Abschaltung=0. Damit ist standardmäßig der bisherige Betriebsmodus mit Impulsgenerator wirksam.
Konfiguration eines neuen OptiY-Experiments
Achtung:
Vor dem Laden des OptiY-Versuchsstandes muss man unbedingt das Modell im SimulationX schließen. Dieses wird von OptiY automatisch geladen, was zu Konflikten führen würde.
OptiY bietet die Möglichkeit, für einen Versuchsstand mehrere Experimente zu verwalten. So können wir die bisherigen Einstellungen und Ergebnisse beibehalten und als Ausgangspunkt für ein neues Experiment nutzen:
- Nach dem Duplizieren des Experiments erscheint im OptiY-Explorer die Kopie als Experiment2.
- Dieses weitere Experiment besitzt am Anfang die gleiche Konfiguration wie das Original. Nur die Anzeigefenster muss man neu definieren.
- Verwaltet man mehrere Experimente in einem Versuchsstand, so sollte man mittels Umbenennen dafür sinnvolle Namen vergeben:
- Das bisheriges Experiment könnte man z.B. nach dem verwendeten Optimierungsverfahren Hooke-Jeeves nennen.
- Für das neue Experiment bietet sich die Bezeichnung Rastersuche 2D an:
Für jedes Experiment wird von OptiY ein separater Workflow verwaltet, so dass darin unabhängig voneinander Änderungen vorgenommen werden können:
- Zuerst selektieren wir die Rastersuche 2D als aktives Experiment mit dem Cursor.
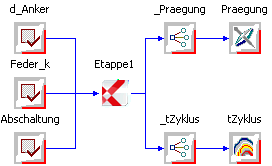
- Wir löschen im zugehörigen Workflow die nicht mehr benötigten Entwurfsparameter:
- Während der Rastersuche muss die Magnetkraft-Erzeugung mit Abschaltung=1 versehen werden:
- Diesen Wert könnte man auch über die globalen Modellparameter des Versuchsstands setzen. Das hat jedoch den Nachteil, dass der Wert für alle Experimente wirkt. Übersieht man diesen Effekt, gelangt man in anderen Experimenten ganz schnell zu fehlerhaften Resultaten!
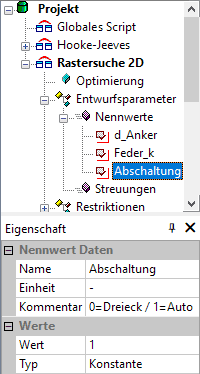
- Wir ergänzen deshalb einen Entwurfsparameter Abschaltung, den wir dann mit dem Startwert=1 versehen, aber konstant halten.
- Abschaltung ordnen wir im Workflow dem Modellparameter Geometrie.Abschaltung zu.
- Die Grenzen der beiden "echten" Entwurfsparameter muss man so groß wählen, dass das globale Optimum im aufgespannten Bereich enthalten ist:
- Ein zu großer Bereich verhindert ein hinreichend dichtes Abtasten der Oberfläche wegen ausufernder Rechenzeit.
- Orientieren sollte man sich an technisch-physikalisch sinnvollen Größen für die Parameter.
- Meist kann man sich günstigen Grenzwerten für die Rastersuche nur iterativ nähern!
- Im Sinne einer effektiven Nutzung der knappen Übungszeit werden hier günstige Grenzwerte vorgegeben:
- d_Anker = 8...16 mm
- Feder_k = 8...200 N/mm
- Als Optimierungsverfahren wählen wir die Rastersuche mit 900 Abtastschritten:
- Der Bereich jedes Entwurfsparameters wird dabei in gleichmäßigen Abständen an 30 Punkten abgetastet.
- 30x30=900 Simulationsläufe sind ein günstiger Kompromiss zwischen Rechenzeit und Feinheit der Abtastung. Auf "betagter" Hardware genügen zur Not auch eine Rasterung von 20x20=400.
- Der Rechenzeitbedarf steigt quadratisch mit der Feinheit der Rasterung!
Hinweis:
In der Simulationssteuerung von SimulationX tStop muss größer gewählt werden, als der längste Prägezyklus im Suchraum! Im Beispiel sollte tStop=10 ms ausreichen.
- Das 3D-Diagramm für das Gütekriterium tZyklus=f(d_Anker, Feder_k) kann man bereits vor dem Start der Optimierung öffnen (Analyse - Darstellung - 3D-Darstellung).
- Nach Start der Optimierung baut sich Stück für Stück die 3D-Fläche im Diagramm auf.
- Ein Mausklick auf das 3D-Diagramm ermöglicht im Eigenschaftsfeld die Konfiguration der Darstellung. Mit dem Einschalten aller Optionen erhält man eine gute Flächendarstellung und erkennt die einzelnen Schritte anhand der Punkte.
- Mit dem Maus-Cursor lässt sich die Darstellung drehen, so dass man sich günstige Ansichten einstellen kann:
Interpretation der Gütefunktion
- Die Magnetkraft schaltet nach Erreichen der Riss-Position ab:
- Reicht die Kraft nicht aus, diese Rissposition zu erreichen, so kehrt die Nadel nicht mehr in die Ruhelage zurück, weil die Kraft nicht abschaltet.
- In diesem Fall wird auf Grund des Messprinzips tZyklus=0 s ermittelt, obwohl praktisch tZyklus=unendlich ist!
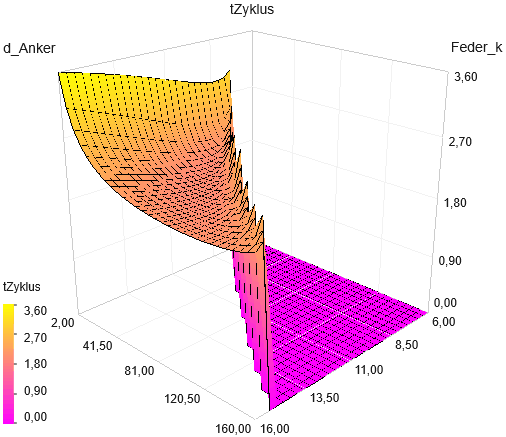
- Die Z-Achse (tZyklus) des 3D-Diagramms wird automatisch zwischen Minimalwert (0 s) und Maximalwert (langsamster Prägezyklus) skaliert:
- tZyklus=0 repräsentiert den verbotenen Bereich, in dem keine Prägung stattfindet (=Restriktionsverletzung)
- Die "Zacken" an der Grenze des zulässigen Lösungsbereichs resultieren aus dem Abtast-Raster.
- Um die abgebildete Gütefunktion mehr den "natürlichen" Gegebenheiten anzupassen und gleichzeitig eine bessere Skalierung in Z-Richtung zu erhalten, genügt eine einfache Änderung:
- Wir setzen für den Anfangswert tZyklus.y0=0.0034 unter den globalen Modellparametern. Damit erscheint dieser Wert von 3,4 ms beim Nichtprägen.
- Man erkennt dann im Bild, dass für diesen Zustand die Zykluszeit steil ansteigt (praktisch gegen Unendlich geht).
- Dieses Plateau markiert gleichzeitig die Forderung für die maximal zulässige Zykluszeit.
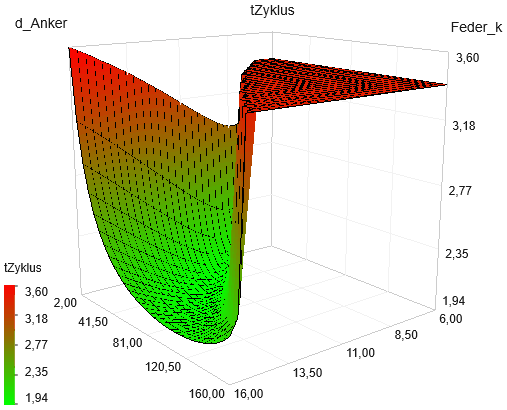
- Nach Rücksetzen und erneutem Start der Rastersuche erhalten wir eine günstigere Darstellung Gütefunktion tZyklus=f(d_Anker, Feder_k):
Das globale Optimum liegt in einer flachen Mulde unweit der Grenze zum "Nichtprägen". Etwas darüber existiert, getrennt durch einen Wall eine weitere flache Mulde mit einem lokalem Minimum. Daraus kann man folgende Schlussfolgerungen ziehen:
- In Abhängigkeit vom gewählten Startpunkt (=Anfangslösung) findet ein lokales Optimierungsverfahren eines der beiden Optima, wovon aber nur eines das globale Optimum darstellt.
- Insbesondere die Federkonstante kann in einem weiten Bereich verändert werden, ohne dass sich die Zykluszeit in relevanten Größenordnungen ändert. Man kann sich bei der Wahl eines konkreten Wertes an der technischen Realisierbarkeit orientieren.
- Zur gewählten Federsteife kann man einen geeigneten Ankerdurchmesser wählen, der einen hinreichend schnellen Prägezyklus ermöglicht.
- Die Kombination der gewählten Entwurfsparametern sollte für eine optimale Lösung möglichst weit entfernt von der Restriktionsgrenze liegen, um trotz aller Toleranzen einen sicheren Betrieb des Antriebs zu gewährleisten.