Software: SimX - Nadelantrieb - Probabilistik - Sample-Methoden: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
|||
| (20 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{DISPLAYTITLE:<span style="position: absolute; clip: rect(1px 1px 1px 1px); clip: rect(1px, 1px, 1px, 1px);">{{FULLPAGENAME}}</span>}} | |||
[[Software:_SimX_-_Nadelantrieb_-_Probabilistische_Simulation|↑]] <div align="center"> [[Software:_SimX_-_Nadelantrieb_-_Probabilistik_-_Toleranzversuchsstand|←]] [[Software:_SimX_-_Nadelantrieb_-_Probabilistik_-_Latin-Hypercube|→]] </div> | [[Software:_SimX_-_Nadelantrieb_-_Probabilistische_Simulation|↑]] <div align="center"> [[Software:_SimX_-_Nadelantrieb_-_Probabilistik_-_Toleranzversuchsstand|←]] [[Software:_SimX_-_Nadelantrieb_-_Probabilistik_-_Latin-Hypercube|→]] </div> | ||
<div align="center">'''Sample-Methoden'''</div> | <div align="center">'''Sample-Methoden (Überblick)'''</div> | ||
{{DISPLAYTITLE:<span style="position: absolute; clip: rect(1px 1px 1px 1px); clip: rect(1px, 1px, 1px, 1px);">{{FULLPAGENAME}}</span>}} | |||
"Sample" ist der englische, auch im Deutschen gebrauchte Begriff für eine [https://de.wikipedia.org/wiki/Stichprobe '''Stichprobe''']. Bei den Sampling-Verfahren der probabilistischen Simulation handelt es sich um stochastische Simulationen mit Zufallszahlen. | |||
Jedes Modell-Exemplar innerhalb der zu simulierenden Stichprobe erhält einen eigenen Parameter-Satz. Die Parameter jedes Modell-Exemplars werden aus den aktuellen Nennwerten (Toleranzmittenwert) und einer "erwürfelten" Abweichung vom Mittenwert entsprechend der zugeordneten Verteilungsdichte-Funktionen ermittelt. Die Anzahl der zu simulierenden Modell-Exemplare entspricht dem Stichprobenumfang. Aus allen Simulationsläufen erhält man die Gesamtverteilung der Ausgangsgrößen (Restriktionen und Gütekriterien). | |||
Dadurch kann man sich eine aufwändige und problemabhängige Herleitung der partiellen Ableitungen z.B. einer komplexen Toleranzkette ersparen. Mit der Sample-Methoden kann man beliebige Toleranzverteilung simulieren. Die Genauigkeit des Verfahrens hängt entscheidend von der Anzahl der Modelldurchrechnungen (Stichprobenumfang) ab, die leider exponentiell zu der Anzahl der Toleranzen steigen muss. Diese Methode ist mit einem hohen Rechenaufwand verbunden, jedoch universell einsetzbar. | |||
Dadurch kann man sich eine aufwändige und problemabhängige Herleitung der partiellen Ableitungen z.B. einer komplexen Toleranzkette ersparen. Mit der Sample-Methoden kann man beliebige Toleranzverteilung simulieren. Die Genauigkeit des Verfahrens hängt entscheidend von der Anzahl der Modelldurchrechnungen (Stichprobenumfang) ab, die leider | |||
In OptiY sind mehrere unterschiedliche Verfahren implementiert. Diese unterscheiden sich vor allem dadurch, wie "intelligent" die Exemplare innerhalb einer Stichprobe "erwürfelt" werden. | In OptiY sind mehrere unterschiedliche Verfahren implementiert. Diese unterscheiden sich vor allem dadurch, wie "intelligent" die Exemplare innerhalb einer Stichprobe "erwürfelt" werden. | ||
== Monte Carlo Sampling == | == Monte Carlo Sampling == | ||
* | [[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_monte-carlo-sampling.gif|right]] | ||
* Bei der [https://de.wikipedia.org/wiki/Monte-Carlo-Simulation '''Monte-Carlo-Simulation'''] wird über die gesamte Toleranzbreite mit "echten" Zufallszahlen "gewürfelt". | |||
* Der erforderliche Stichprobenumfang N für eine angestrebte "saubere" Verteilungsfunktion der Toleranzgrößen ist deshalb relativ hoch! | * Der erforderliche Stichprobenumfang N für eine angestrebte "saubere" Verteilungsfunktion der Toleranzgrößen ist deshalb relativ hoch! | ||
* Erst bei einer Stichprobengröße von ca. N=1 000 000 konvergiert der Fehler dieser Toleranzsimulation gegen Null! | * Erst bei einer Stichprobengröße von ca. N=1 000 000 konvergiert der Fehler dieser Toleranzsimulation gegen Null! | ||
* Bei N=50 wird eine Normalverteilung z.B. nur ungenau nachgebildet | * Bei N=50 wird eine Normalverteilung z.B. nur ungenau nachgebildet (Bild rechts). | ||
== Latin Hypercube Sampling == | == Latin Hypercube Sampling == | ||
* Im Unterschied zum "Monte Carlo Sampling" wird die gesamte Toleranzbreite eines streuenden Parameters in Teilintervalle zerlegt. | * Im Unterschied zum klassischen "Monte Carlo Sampling" wird beim [https://www.statsoft.de/glossary/L/LatinHypercubeSampling.htm '''Latin Hypercube Sampling'''] die gesamte Toleranzbreite eines streuenden Parameters in Teilintervalle zerlegt. | ||
* Jedes Teilintervall wird je nach vorgegebener Verteilungsfunktion mit Zufallszahlen gefüllt. | * Jedes Teilintervall wird je nach vorgegebener Verteilungsfunktion mit Zufallszahlen gefüllt. | ||
* Deshalb wird eine "saubere" Verteilungsfunktion mit relativ kleinem Stichprobenumfang erreicht (Beispiel Normalverteilung N=50): | * Deshalb wird eine "saubere" Verteilungsfunktion mit relativ kleinem Stichprobenumfang erreicht (Beispiel Normalverteilung N=50): | ||
| Zeile 26: | Zeile 25: | ||
== Sobol Sampling == | == Sobol Sampling == | ||
* Das Verfahren nutzt im Unterschied zur "reinen" Monte-Carlo-Simulation (1. Bild) eine Quasi-Zufallszahlen-Sequenz (2. Bild). | * Das Verfahren nutzt im Unterschied zur "reinen" Monte-Carlo-Simulation (1. Bild) eine [https://de.wikipedia.org/wiki/Pseudozufall '''Quasi-Zufallszahlen-Sequenz'''] (2. Bild). | ||
* Durch Ausnutzung von Symmetriebeziehungen erfolgt eine gleichmäßigere Verteilung der Punktwolke im Parameterraum. | * Durch Ausnutzung von Symmetriebeziehungen erfolgt eine gleichmäßigere Verteilung der Punktwolke im Parameterraum. | ||
* Damit benötigt das Verfahren für die gleiche Genauigkeit nur ca. 1/10 der Stichprobengröße | * Damit benötigt das Verfahren für die gleiche Genauigkeit nur ca. 1/10 der Stichprobengröße:<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_monte-carlo-wolke.gif| ]] [[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_sobol-punktwolke.gif| ]]</div> | ||
<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_monte-carlo-wolke.gif| ]] [[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_sobol-punktwolke.gif| ]]</div> | |||
== Response Surface Methode (Virtuelle Stichprobe) == | == Response Surface Methode (Virtuelle Stichprobe) == | ||
Als direktes Ergebnis der Stichproben-Simulation mittels Sampling-Methode liegt eine Punktwolke vor, welche die Verknüpfung zwischen den streuenden Entwurfsparametern und den Ergebnisgrößen (Gütekriterien, Restriktionen) repräsentiert: | Als direktes Ergebnis der Stichproben-Simulation mittels Sampling-Methode liegt eine Punktwolke vor, welche die Verknüpfung zwischen den streuenden Entwurfsparametern und den Ergebnisgrößen (Gütekriterien, Restriktionen) repräsentiert: | ||
* Geht man davon aus, dass zwischen den Parametern und Ergebnisgrößen ein stetiger funktioneller Zusammenhang besteht, so kann man diesen durch eine Approximationsfunktion abbilden. | * Geht man davon aus, dass zwischen den Parametern und Ergebnisgrößen ein stetiger funktioneller Zusammenhang besteht, so kann man diesen durch eine Approximationsfunktion abbilden. | ||
* Im OptiY können [ | * Im OptiY werden drei Verfahren für die Approximation bereitgestellt: '''''Polynomial''''', [https://de.wikipedia.org/wiki/Gauss-Prozess '''''Gauss Prozess'''''] und [https://de.wikipedia.org/wiki/Kriging '''''Adaptiver Gauss Prozess''''']. | ||
* Wir nutzen in dieser Übung die standardmäßig eingestellte ''Polynomiale Approximation''. Damit können [https://de.wikipedia.org/wiki/Polynom '''Polynome'''] beliebiger Ordnung als Approximationsfunktion für jede Ergebnisgröße verwendet werden: | |||
:<math>P(x) = \sum_{i=0}^n a_ix^i = a_nx^n + a_{n-1}x^{n-1} + \cdots + a_2x^2 + a_1x + a_0</math> | :<math>P(x) = \sum_{i=0}^n a_ix^i = a_nx^n + a_{n-1}x^{n-1} + \cdots + a_2x^2 + a_1x + a_0</math> | ||
* Durch Anwendung der [ | * Durch Anwendung der [https://de.wikipedia.org/wiki/Methode_der_kleinsten_Fehlerquadrate '''Methode der kleinsten Fehlerquadrate'''] werden die Parameter der Polynome so bestimmt, dass die Approximationsfunktionen möglichst gut in die Punktwolke der "gesampelten" Stichprobe passen. | ||
* Die minimal erforderliche Anzahl der Modellberechnungen '''M''' (=Stichprobengröße) ergibt sich aus der Anzahl '''n''' der stochastischen Variablen und der gewählten Ordnung '''O''' der Polynom-Funktion zu '''M=(n²-n)/2+O*n+1''' | * Die minimal erforderliche Anzahl der Modellberechnungen '''M''' (=Stichprobengröße) ergibt sich aus der Anzahl '''n''' der stochastischen Variablen und der gewählten Ordnung '''O''' der Polynom-Funktion zu <div align="center">'''M=(n²-n)/2+O*n+1'''</div> | ||
Die mittels dieser Ausgleichsrechnung ermittelten Ersatzfunktionen (ein Polynom pro Ergebnisgröße), kann man | Die mittels dieser Ausgleichsrechnung ermittelten Ersatzfunktionen (ein Polynom pro Ergebnisgröße), kann man in der statistischen Auswertung als Grundlage für eine "virtuelle Stichprobe" benutzen. Man spricht auch von der "Response Surface Methode" (RSM), weil die Ersatzfunktionen wie Flächen über dem Parameter-Raum aufgespannt sind. Diese Funktionsflächen liefern ersatzweise die Systemantwort für die eingespeiste Parameter-Kombination. | ||
* '''Vorteil''' | * '''Vorteil''' | ||
** Auf die Ersatzfunktionen | ** Auf die Ersatzfunktionen können die gleichen Sample-Methoden angewandt werden, wie zuvor auf das Originalmodell. | ||
** Der Umfang einer virtuellen Stichprobe kann sehr groß gewählt werden, da die Ersatzfunktionen um Größenordnungen schneller als die Originalmodelle rechnen. | ** Der Umfang einer virtuellen Stichprobe kann sehr groß gewählt werden, da die Ersatzfunktionen um Größenordnungen schneller als die Originalmodelle rechnen. | ||
** Damit können statistischen Aussagen zu den Ersatzfunktionen praktisch mit beliebiger Genauigkeit gewonnen werden. | ** Damit können statistischen Aussagen zu den Ersatzfunktionen praktisch mit beliebiger Genauigkeit gewonnen werden. | ||
* '''Nachteil''' | * '''Nachteil''' | ||
** Eigentlich interessieren den Anwender nicht die Aussagen zur Ersatzfunktion, sondern die Eigenschaften des zu untersuchenden Originals. Die Genauigkeit der statistischen Aussagen in Bezug auf das Originalmodell wird überwiegend durch die Genauigkeit der Approximationsfunktionen bestimmt. | ** Eigentlich interessieren den Anwender nicht die Aussagen zur Ersatzfunktion, sondern die Eigenschaften des zu untersuchenden Originals. Die Genauigkeit der statistischen Aussagen in Bezug auf das Originalmodell wird überwiegend durch die Genauigkeit der Approximationsfunktionen bestimmt. | ||
** Die Residuen der Ausgleichsrechnung für eine vorliegende Stichprobe zeigen nur, wie genau die die Ausgleichsfläche in die vorhandene Punktwolke passt. | ** Die [https://de.wikipedia.org/wiki/Residuum_(Numerische_Mathematik) '''Residuen'''] der Ausgleichsrechnung für eine vorliegende Stichprobe zeigen nur, wie genau die die Ausgleichsfläche in die vorhandene Punktwolke passt. | ||
** Informationen zur Genauigkeit der Ausgleichsfläche in den Zwischenräumen der Punktwolke sind | ** Informationen zur Genauigkeit der Ausgleichsfläche in den Zwischenräumen der Punktwolke sind mit dem Polynom-Ansatz nicht zu gewinnen. | ||
** Es ist somit schwierig, statistisch gesicherte Aussagen zum Originalmodell für kleine Fehlerintervalle zu erhalten. | ** Es ist somit schwierig, statistisch gesicherte Aussagen zum Originalmodell für kleine Fehlerintervalle zu erhalten. | ||
| Zeile 52: | Zeile 51: | ||
* Man darf nie vergessen, dass ein Originalmodell auch nur ein fehlerbehafteter Ersatz für das eigentlich zu untersuchende Original darstellt. | * Man darf nie vergessen, dass ein Originalmodell auch nur ein fehlerbehafteter Ersatz für das eigentlich zu untersuchende Original darstellt. | ||
* Modellbasierte statistische Aussagen im Promille-Bereich sind in Bezug auf das Original immer sehr skeptisch zu betrachten! | * Modellbasierte statistische Aussagen im Promille-Bereich sind in Bezug auf das Original immer sehr skeptisch zu betrachten! | ||
* Die Response Surface Methode erzeugt hier eine weitere Modell-Hierarchie im Experimentierprozess. | * Die ''Response Surface Methode'' erzeugt hier eine weitere Modell-Hierarchie im Experimentierprozess. | ||
<div align="center"> [[Software:_SimX_-_Nadelantrieb_-_Probabilistik_-_Toleranzversuchsstand|←]] [[Software:_SimX_-_Nadelantrieb_-_Probabilistik_-_Latin-Hypercube|→]] </div> | <div align="center"> [[Software:_SimX_-_Nadelantrieb_-_Probabilistik_-_Toleranzversuchsstand|←]] [[Software:_SimX_-_Nadelantrieb_-_Probabilistik_-_Latin-Hypercube|→]] </div> | ||
Aktuelle Version vom 27. November 2019, 10:00 Uhr
"Sample" ist der englische, auch im Deutschen gebrauchte Begriff für eine Stichprobe. Bei den Sampling-Verfahren der probabilistischen Simulation handelt es sich um stochastische Simulationen mit Zufallszahlen.
Jedes Modell-Exemplar innerhalb der zu simulierenden Stichprobe erhält einen eigenen Parameter-Satz. Die Parameter jedes Modell-Exemplars werden aus den aktuellen Nennwerten (Toleranzmittenwert) und einer "erwürfelten" Abweichung vom Mittenwert entsprechend der zugeordneten Verteilungsdichte-Funktionen ermittelt. Die Anzahl der zu simulierenden Modell-Exemplare entspricht dem Stichprobenumfang. Aus allen Simulationsläufen erhält man die Gesamtverteilung der Ausgangsgrößen (Restriktionen und Gütekriterien).
Dadurch kann man sich eine aufwändige und problemabhängige Herleitung der partiellen Ableitungen z.B. einer komplexen Toleranzkette ersparen. Mit der Sample-Methoden kann man beliebige Toleranzverteilung simulieren. Die Genauigkeit des Verfahrens hängt entscheidend von der Anzahl der Modelldurchrechnungen (Stichprobenumfang) ab, die leider exponentiell zu der Anzahl der Toleranzen steigen muss. Diese Methode ist mit einem hohen Rechenaufwand verbunden, jedoch universell einsetzbar.
In OptiY sind mehrere unterschiedliche Verfahren implementiert. Diese unterscheiden sich vor allem dadurch, wie "intelligent" die Exemplare innerhalb einer Stichprobe "erwürfelt" werden.
Monte Carlo Sampling
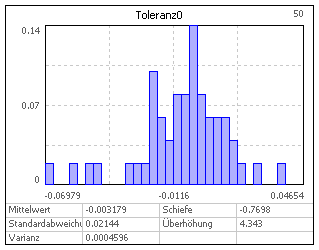
- Bei der Monte-Carlo-Simulation wird über die gesamte Toleranzbreite mit "echten" Zufallszahlen "gewürfelt".
- Der erforderliche Stichprobenumfang N für eine angestrebte "saubere" Verteilungsfunktion der Toleranzgrößen ist deshalb relativ hoch!
- Erst bei einer Stichprobengröße von ca. N=1 000 000 konvergiert der Fehler dieser Toleranzsimulation gegen Null!
- Bei N=50 wird eine Normalverteilung z.B. nur ungenau nachgebildet (Bild rechts).
Latin Hypercube Sampling
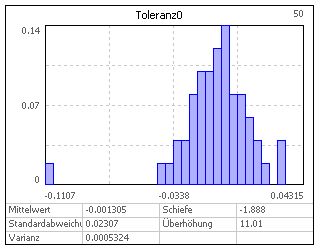
- Im Unterschied zum klassischen "Monte Carlo Sampling" wird beim Latin Hypercube Sampling die gesamte Toleranzbreite eines streuenden Parameters in Teilintervalle zerlegt.
- Jedes Teilintervall wird je nach vorgegebener Verteilungsfunktion mit Zufallszahlen gefüllt.
- Deshalb wird eine "saubere" Verteilungsfunktion mit relativ kleinem Stichprobenumfang erreicht (Beispiel Normalverteilung N=50):
Sobol Sampling
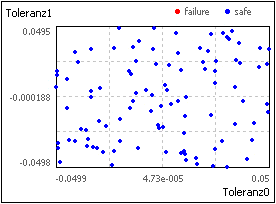
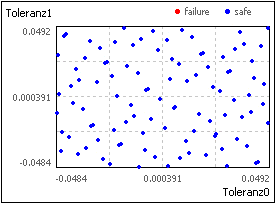
- Das Verfahren nutzt im Unterschied zur "reinen" Monte-Carlo-Simulation (1. Bild) eine Quasi-Zufallszahlen-Sequenz (2. Bild).
- Durch Ausnutzung von Symmetriebeziehungen erfolgt eine gleichmäßigere Verteilung der Punktwolke im Parameterraum.
- Damit benötigt das Verfahren für die gleiche Genauigkeit nur ca. 1/10 der Stichprobengröße:
Response Surface Methode (Virtuelle Stichprobe)
Als direktes Ergebnis der Stichproben-Simulation mittels Sampling-Methode liegt eine Punktwolke vor, welche die Verknüpfung zwischen den streuenden Entwurfsparametern und den Ergebnisgrößen (Gütekriterien, Restriktionen) repräsentiert:
- Geht man davon aus, dass zwischen den Parametern und Ergebnisgrößen ein stetiger funktioneller Zusammenhang besteht, so kann man diesen durch eine Approximationsfunktion abbilden.
- Im OptiY werden drei Verfahren für die Approximation bereitgestellt: Polynomial, Gauss Prozess und Adaptiver Gauss Prozess.
- Wir nutzen in dieser Übung die standardmäßig eingestellte Polynomiale Approximation. Damit können Polynome beliebiger Ordnung als Approximationsfunktion für jede Ergebnisgröße verwendet werden:
- [math]\displaystyle{ P(x) = \sum_{i=0}^n a_ix^i = a_nx^n + a_{n-1}x^{n-1} + \cdots + a_2x^2 + a_1x + a_0 }[/math]
- Durch Anwendung der Methode der kleinsten Fehlerquadrate werden die Parameter der Polynome so bestimmt, dass die Approximationsfunktionen möglichst gut in die Punktwolke der "gesampelten" Stichprobe passen.
- Die minimal erforderliche Anzahl der Modellberechnungen M (=Stichprobengröße) ergibt sich aus der Anzahl n der stochastischen Variablen und der gewählten Ordnung O der Polynom-Funktion zu M=(n²-n)/2+O*n+1
Die mittels dieser Ausgleichsrechnung ermittelten Ersatzfunktionen (ein Polynom pro Ergebnisgröße), kann man in der statistischen Auswertung als Grundlage für eine "virtuelle Stichprobe" benutzen. Man spricht auch von der "Response Surface Methode" (RSM), weil die Ersatzfunktionen wie Flächen über dem Parameter-Raum aufgespannt sind. Diese Funktionsflächen liefern ersatzweise die Systemantwort für die eingespeiste Parameter-Kombination.
- Vorteil
- Auf die Ersatzfunktionen können die gleichen Sample-Methoden angewandt werden, wie zuvor auf das Originalmodell.
- Der Umfang einer virtuellen Stichprobe kann sehr groß gewählt werden, da die Ersatzfunktionen um Größenordnungen schneller als die Originalmodelle rechnen.
- Damit können statistischen Aussagen zu den Ersatzfunktionen praktisch mit beliebiger Genauigkeit gewonnen werden.
- Nachteil
- Eigentlich interessieren den Anwender nicht die Aussagen zur Ersatzfunktion, sondern die Eigenschaften des zu untersuchenden Originals. Die Genauigkeit der statistischen Aussagen in Bezug auf das Originalmodell wird überwiegend durch die Genauigkeit der Approximationsfunktionen bestimmt.
- Die Residuen der Ausgleichsrechnung für eine vorliegende Stichprobe zeigen nur, wie genau die die Ausgleichsfläche in die vorhandene Punktwolke passt.
- Informationen zur Genauigkeit der Ausgleichsfläche in den Zwischenräumen der Punktwolke sind mit dem Polynom-Ansatz nicht zu gewinnen.
- Es ist somit schwierig, statistisch gesicherte Aussagen zum Originalmodell für kleine Fehlerintervalle zu erhalten.
Hinweis:
- Man darf nie vergessen, dass ein Originalmodell auch nur ein fehlerbehafteter Ersatz für das eigentlich zu untersuchende Original darstellt.
- Modellbasierte statistische Aussagen im Promille-Bereich sind in Bezug auf das Original immer sehr skeptisch zu betrachten!
- Die Response Surface Methode erzeugt hier eine weitere Modell-Hierarchie im Experimentierprozess.