Software: SimX - Nadelantrieb - Probabilistik - Latin-Hypercube: Unterschied zwischen den Versionen
K (→Anthill-Plot) |
K (→Restriktionen) |
||
| (54 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Software:_SimX_-_Nadelantrieb_-_Probabilistische_Simulation|↑]] <div align="center"> [[Software:_SimX_-_Nadelantrieb_-_Probabilistik_-_Sample-Methoden|←]] [[Software:_SimX_-_Nadelantrieb_-_Probabilistik_-_Moment-Methoden|→]] </div> | |||
[[Software:_SimX_-_Nadelantrieb_-_Probabilistische_Simulation| | |||
<div align="center">'''Latin Hypercube (Experimente)'''</div> | <div align="center">'''Latin Hypercube (Experimente)'''</div> | ||
'''''Wichtig:''''' Falls es noch nicht geschehen ist - man muss '''Simulation als Optimierungsverfahren''' wählen!<br> | |||
== Versuchsplanung == | == Versuchsplanung == | ||
''''' | Das "Latin Hypercube Sampling" ist ein geeignetes Zufallsverfahren, um in unserem Beispiel mit akzeptablem Berechnungsaufwand hinreichend genaue und anschauliche Ergebnisse zu erhalten: | ||
* Im ''OptiY'' ist das voreingestellte Standard-Verfahren als "Latin Hypercube Sampling" konfiguriert. | |||
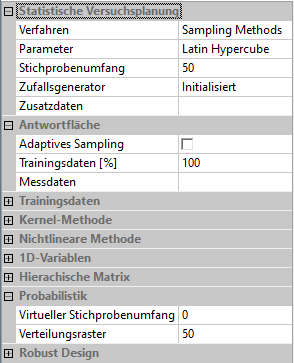
* Wählen wir als Verfahren manuell die "Sampling Methode", so werden zusätzlich der standardmäßige Stichproben-Umfang und die Konfiguration des Zufallsgenerator sichtbar:<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_versuchsplanung_latin-hypercube.gif|.]] </div> | |||
Leider wird sogar bei dem voreingestellten Standard-Verfahren der Anwender mit einer Vielzahl von Konfigurationsmöglichkeiten konfrontiert, welche nur in speziellen Szenarien erforderlich sind. Wir möchten nur eine Toleranzanalyse für wenige Streuungen auf der Basis von Modellberechnungen durchführen. Deshalb werden im Folgenden alle Eingabefelder minimiert, deren Parameter dafür nicht nötig sind: | |||
<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_Versuchsplanung_Standard_Parameter.gif|.]] </div> | |||
Die minimierten (hier nicht benötigten) Eingabefelder konfigurieren folgende Aspekte: | |||
* '''Trainingsdaten''': Auswahlmethode für Menge der Trainingsdaten für das Meta-Modell, wenn nicht alle Modellabtastungen für die Identifikation dieser Ersatzfunktion verwendet werden. | |||
* '''Kernel-Methode''': ermöglicht es durch Transformationen von Datensätzen in höher dimensionale Räume, "ähnliche" Datenpunkte durch lineare Funktionen in Cluster zu separieren (z.B. erforderlich bei Meta-Modellen mit Cluster-Bildung) | |||
* '''Nichtlineare Methode''': wie die Kernel-Methode ein Ansatz des maschinellen Lernens, allerdings mit nichtlinearen Funktionen zur Cluster-Bildung. | |||
* '''1D-Variable''': 1D-Variable sind spezielle Daten-Elemente, welche anstatt einzelner Werte dynamische Signale in der Form von Y=f(X) enthalten. | |||
* '''Hierarchische Matrix''': Konfiguration der Matrixberechnung auf einen GPU bei großen Datenmengen. | |||
* '''Robust Design''': Konfiguration der probabilistischen Optimierung unter Nutzung des Meta-Modells | |||
Wir werden uns in dieser Übungsetappe auf das Verstehen der Grundlagen der Sample-Methode konzentrieren. Deshalb beschränken wir uns auf Polynom-Funktionen als einfachsten Ansatz für ein Meta-Modell: | |||
* Die minimal erforderliche Anzahl der Modellberechnungen '''M''' (=Stichprobenumfang) ergibt sich aus der Anzahl '''n''' der stochastischen Variablen und der gewählten Ordnung '''O''' der Polynom-Funktion zu '''M=(n²-n)/2+O*n+1'''. | |||
* Wir werden für die Ersatzfunktionen Polynome 2. Ordnung benutzen. Damit benötigt man im Beispiel bei 5 Streuungen minimal '''M=21''' Modellberechnungen. | |||
* Da das Polynom 2. Ordnung nicht exakt die wirkliche Übertragungsfunktion im Streubereich nachbildet, muss mittels der Methode der kleinsten Fehlerquadrate eine optimal zu den Datenpunkten passende Ausgleichsfunktion gefunden werden. | |||
* Die Genauigkeit der ermittelten Polynom-Ausgleichsfunktion steigt mit der Anzahl der verfügbaren Datenpunkte. | |||
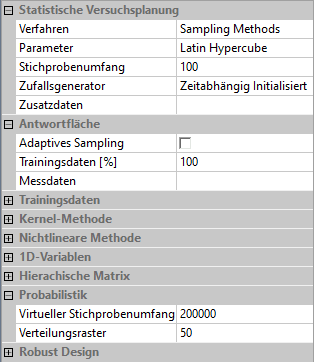
'''Konfiguration der "realen" und "virtuellen" Stichprobe:'''[[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_Versuchsplanung_Latin_Hypercube.gif|right]] | |||
* Ein '''Stichprobenumfang=100''' für die Gewinnung der "realen" Datensätze ist im Beispiel ein guter Kompromiss zwischen Berechnungsaufwand und Genauigkeit. | |||
* | * Entscheidend für die Reproduzierbarkeit der Ergebnisse ist die Konfiguration des Zufallszahlengenerators. Dieser produziert nach seiner Initialisierung immer die gleiche Sequenz von Zahlen. Indem man den Zeitpunkt der Initialisierung steuert, kann man unterschiedliche Effekte erzielen: | ||
* | |||
*# '''''Initialisiert'''''<br>Bewirkt eine Initialisierung mit dem Wert=1 beim Start einer jeden neuen Toleranz-Simulation, d.h. für die Berechnung jeder neuen Stichprobe. Bei gleichen Nennwerten erhält man also bei der Berechnung jeder Stichprobe exakt die gleichen Simulationsergebnisse. | *# '''''Initialisiert'''''<br>Bewirkt eine Initialisierung mit dem Wert=1 beim Start einer jeden neuen Toleranz-Simulation, d.h. für die Berechnung jeder neuen Stichprobe. Bei gleichen Nennwerten erhält man also bei der Berechnung jeder Stichprobe exakt die gleichen Simulationsergebnisse. | ||
*# '''''Zeitabhängig initialisiert'''''<br>Bewirkt eine Initialisierung mit einem Wert=f(Maschinenzeit) beim Start einer jeden neuen Toleranz-Simulation. Damit sind die Ergebnisse auch bei gleichen Nennwerten von Simulation zu Simulation unterschiedlich, weil der Startpunkt des Zufallsgenerators zeitabhängig ist. Dies widerspiegelt sicher am besten die praktisch mögliche Bandbreite von Stichproben-Ergebnissen | *# '''''Zeitabhängig initialisiert'''''<br>Bewirkt eine Initialisierung mit einem Wert=f(Maschinenzeit) beim Start einer jeden neuen Toleranz-Simulation. Damit sind die Ergebnisse auch bei gleichen Nennwerten von Simulation zu Simulation unterschiedlich, weil der Startpunkt des Zufallsgenerators zeitabhängig ist. Dies widerspiegelt sicher am besten die praktisch mögliche Bandbreite von Stichproben-Ergebnissen und wird deshalb gewählt! | ||
*# '''''Nicht initialisiert'''''<br>Bewirkt eine einmalige Initialisierung mit dem Wert=1 beim Start des Programms OptiY. Startet man danach ein gespeichertes Experiment, so erzielt man damit immer die gleichen Ergebnisse. Damit lassen sich Toleranzbehaftete Experimente zu unterschiedlichen Zeiten auch auf unterschiedlichen Computern reproduzieren. Da die Zufallszahlen von allen vorhergehenden Vorgängen abhängig sind, erfordert eine Experiment-Reproduktion jedoch immer den vorherigen Neustart von OptiY! | *# '''''Nicht initialisiert'''''<br>Bewirkt eine einmalige Initialisierung mit dem Wert=1 beim Start des Programms OptiY. Startet man danach ein gespeichertes Experiment, so erzielt man damit immer die gleichen Ergebnisse. Damit lassen sich Toleranzbehaftete Experimente zu unterschiedlichen Zeiten auch auf unterschiedlichen Computern reproduzieren. Da die Zufallszahlen von allen vorhergehenden Vorgängen abhängig sind, erfordert eine Experiment-Reproduktion jedoch immer den vorherigen Neustart von OptiY! | ||
* | * Die gewählte Initialisierungsart für den Zufallszahlengenerator wirkt auch für die "virtuelle" Stichprobe. | ||
* Ein '''Virtueller Stichprobenumfang= | * Ein '''Virtueller Stichprobenumfang=200000''' auf der aus der Approximationsfunktion gebildeten Antwortfläche ist ein guter Kompromiss zwischen Berechnungszeit und statistischer Genauigkeit. | ||
* Das '''Verteilungsraster=50''' definiert, wie eckig bzw. geglättet die probabilistischen Ergebnisse grafisch dargestellt werden (z.B. die Verteilungsdichtefunktionen). | |||
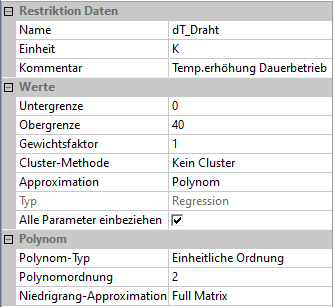
[[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_versuchsplanung_approximationsfunktionen.gif|right]] | '''Approximationsfunktion:'''[[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_versuchsplanung_approximationsfunktionen.gif|right]] | ||
* Die Auswahl der Approximationsfunktionen ("Antwortflächen") für die Durchführung der virtuellen Stichprobe ist eigentlich Bestandteil der Versuchsplanung. | * Die Auswahl der Approximationsfunktionen ("Antwortflächen") für die Durchführung der virtuellen Stichprobe ist eigentlich Bestandteil der Versuchsplanung. | ||
* Für jede Bewertungsgröße des Modells (Restriktion bzw. Gütekriterium) kann jedoch eine individuelle Approximationsfunktion gewählt werden. | * Für jede Bewertungsgröße des Modells (Restriktion bzw. Gütekriterium) kann jedoch eine individuelle Approximationsfunktion gewählt werden. | ||
* Deshalb erfolgt für jede Bewertungsgröße getrennt die Wahl der Approximation. Im Beispiel wählen wir für alle Restriktionen einheitlich '''Polynomiale Approximation''' mit der '''Ordnung=2'''. | * Deshalb erfolgt für jede Bewertungsgröße getrennt die Wahl der Approximation. Im Beispiel wählen wir für alle Restriktionen einheitlich '''Polynomiale Approximation''' mit der '''Ordnung=2'''. | ||
* '''Polynom-Typ = Einheitliche Ordnung''' bedeutet dabei die Verwendung der gleichen Polynomordnung in Richtung der Koordinatenachse jeder Streuung. Die unterschiedliche Wirkung einer Streuung auf eine Restriktionsgröße könnte man auch durch unterschiedliche Polynomordnungen in jede Streuungsrichtung berücksichtigen. | |||
* Standardmäßig werden alle Parameter (=Streuungen) in die Approximation der Ersatzfunktion einbezogen → im Beispiel:<br>'''dT_Draht = f(T_Spule, d_Papier, v_el; Re_Eisen, kFeder_rel)''' | |||
'''''Hinweis:''''': | |||
* Mit diesem quadratischen Ansatz können auch monotone Krümmungen im betrachteten Bereich des Parameterraumes nachgebildet werden. | * Mit diesem quadratischen Ansatz können auch monotone Krümmungen im betrachteten Bereich des Parameterraumes nachgebildet werden. | ||
* | * Es muss hier nur der sehr kleine Streubereich um die Toleranzmittenwerte nachgebildet werden. Die globalen Nichtlinearitäten des Originalmodells spielen dabei meist keine Rolle! | ||
== Visualisierung und Interpretation == | == Visualisierung und Interpretation == | ||
| Zeile 35: | Zeile 53: | ||
* Die Ergebnisse der Stichproben-Simulation werden umso genauer, je weiter man innerhalb der Stichprobe voranschreitet. | * Die Ergebnisse der Stichproben-Simulation werden umso genauer, je weiter man innerhalb der Stichprobe voranschreitet. | ||
=== Streuende Parameter === | |||
= | Zusätzlich zu den Streuungen wurde als Ergänzung zur normierten Feder-Toleranz '''kFeder_rel''' die daraus berechnete absolute Feder-Toleranz '''kFeder''' (Restriktionsgröße ohne Wirkung) als Histogramm abgebildet: | ||
* In den Histogrammen kann man überprüfen, ob die Streuungen sich in den vorgesehenen Grenzen bewegen. | |||
* Dabei muss man beachten, dass es für Normalverteilungen keine festen Grenzen gibt und einige Exemplare der Stichprobe außerhalb der vorgegebenen Grenzen liegen können! | |||
* Im Verlaufe der Berechnung kann man qualitativ beurteilen, ob der "reale" Stichproben-Umfang für eine "saubere" Verteilungsdichte ausreicht. | |||
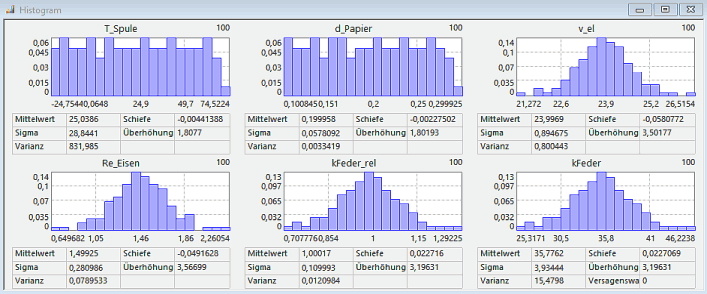
* In den Histogrammen werden nur die Modellberechnungen der "realen" Stichprobe dargestellt: | |||
<div align="center">[[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_histogramme_toleranzen.gif|.]]</div> | |||
Unmittelbar nach der Simulation der "realen" Stichprobe werden die Übertragungsfunktionen (Antwortflächen) der Bewertungsgrößen auf Basis der gewählten Approximationsfunktionen berechnet. Mit diesem Ersatzmodell erfolgt dann die Simulation der "virtuellen" Stichprobe: | |||
Unmittelbar nach der Simulation der "realen" Stichprobe werden die Übertragungsfunktionen (Antwortflächen) der Bewertungsgrößen auf Basis der gewählten Approximationsfunktionen berechnet. Mit diesem Ersatzmodell erfolgt dann die Simulation der "virtuellen" Stichprobe | |||
* Die Punkte der realen Stichprobe werden bei der Auswertung der virtuellen Stichprobe zusätzlich berücksichtigt. Die darin enthaltene Information geht somit nicht verloren. | * Die Punkte der realen Stichprobe werden bei der Auswertung der virtuellen Stichprobe zusätzlich berücksichtigt. Die darin enthaltene Information geht somit nicht verloren. | ||
* | * Infolge des extremen Stichprobenumfanges (im Beispiel 200 000) ist es möglich, auch für die streuenden Parameter "geglättete" Verteilungsdichtefunktionen zu generieren. | ||
* Bei den statistischen Kenngrößen gibt es Abweichungen zwischen der realen und der virtuellen Stichprobe. Die Größe der Abweichungen wird im Wesentlichen durch den Umfang der realen Stichprobe bestimmt. Letztendlich bestimmt diese das Vertrauensintervall der statistischen Aussagen! | * Für die Bewertungsgrößen liegen im Ergebnisse der virtuellen Stichprobe ebenfalls die Verteilungsdichtefunktionen vor. Somit können wir jetzt auch die absolute Verteilungsdichte der Federsteife darstellen. | ||
* In Analogie zu den Histogrammen öffnen wir alle zugehörigen Verteilungsdichte-Darstellungen ( '''''Analyse > Probabilistik > Verteilungsdichte''''' ): | |||
<div align="center">[[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_verteilungsdichten_toleranzen.gif|.]]</div> | |||
* Bei den statistischen Kenngrößen gibt es Abweichungen zwischen der realen und der virtuellen Stichprobe. Die Größe der Abweichungen wird im Wesentlichen durch den Umfang der realen Stichprobe bestimmt. Letztendlich bestimmt diese das Vertrauensintervall der statistischen Aussagen! | |||
'''''Hinweis:''''' Im OptiY werden Ersatzfunktionen (Antwortflächen) nur für die Bewertungsgrößen approximiert. Für alle anderen Ergebnisgrößen (z.B. Ausgangsgrößen) des Experiment-Workflows stehen nur die Werte der "realen" Stichprobe zur Verfügung. Deren Streuung kann man in Histogrammen darstellen. | |||
=== | === Restriktionen === | ||
Man erkennt in den entsprechenden Histogrammen schon während der Stichproben-Berechnung, in welchem Maße Restriktionen verletzt werden. Kritisch sind im Beispiel die Abschaltspannungen, welche im Beispiel über '''800 V''' erreichen und wahrscheinlich zusammen mit Stromspitzen von ca. '''4 A''' auftreten: | |||
<div align="center">[[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_histogramme_restriktionen.gif|.]]</div> | |||
=== | '''<u>Histogramm-Eigenschaften</u>:''' | ||
* Man kann mehrere Histogramme in einem Histogramm-Fenster darstellen. | |||
* Die X-Achse ist standardmäßig in 50 Bereiche (Balken) aufgeteilt. | |||
* Die Höhe der Balken repräsentiert auf der Y-Achse die anteilige Häufigkeit der Stichprobenpunkte im jeweiligen Intervall. | |||
* Weitere Informationen wie [https://de.wikipedia.org/wiki/Mittelwert '''Mittelwert'''], [https://de.wikipedia.org/wiki/Schiefe_(Statistik) '''Schiefe'''], [https://en.wikipedia.org/wiki/Kurtosis '''Überhöhung'''], [https://de.wikipedia.org/wiki/Varianz '''Varianz'''] und [https://de.wikipedia.org/wiki/Standardabweichung '''Standardabweichung'''] stehen zur Verfügung. | |||
* Bei Restriktionen wird auch die Teil-Versagenswahrscheinlichkeit bezüglich der dargestellten Restriktionsgröße angezeigt. | |||
* Bereiche mit Restriktionsverletzungen werden markiert. | |||
Wählt man mit dem Cursor ein Histogramm aus, so erscheinen die Histogramm-Eigenschaften im Eigenschaftsfenster: | |||
<div align="center">[[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_histogramm-eigenschaft.gif|.]]</div> | |||
* Die Eigenschaften beziehen sich auf alle Histogramme des gewählten Histogramm-Fensters, auch wenn der Name eines konkreten Histogramms angezeigt wird. | |||
* Man kann die Anzahl der Balken verändern. Wählt man ''Dichte als Y-Achse=Falsch'', so wird die Anzahl der im einzelnen Balken enthaltenen Stichproben-Exemplare angezeigt. | |||
* Die Grenzen der X-Achse werden standardmäßig durch ''Auto-Skalierung=Wahr'' ermittelt. Wählt man ''Auto-Skalierung=Falsch'', so kann man die Grenzen (Min, Max) für das gewählte Histogramm manuell einstellen. | |||
Auch bei den Verteilungsdichten der Restriktionen sind Bereiche mit unzulässigen Werten markiert. So erhält man einen qualitativen Eindruck, in welchem Maße Restriktionen verletzt werden. Zusätzlich steht der Wert der Teilversagenswahrscheinlichkeit unterhalb der Grafik zusammen mit der Gesamtversagenswahrscheinlichkeit: | |||
<div align="center">[[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_verteilungsdichten_restriktionen.gif|.]]</div> | |||
Wie exakt die Approximationsfunktionen der Ausgangsgrößen an die Punkte der realen Stichprobe angepasst wurden, kann man mittels der Residual-Diagramme überprüfen ('''''Analyse > Antwortflächen > Residuum Plot''''' - Drag&Drop der Restriktionen/Gütekriterien): | |||
<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_verteilungsdichten_restriktionen.gif| ]] </div> | <div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_residual-plot.gif| ]] </div> | ||
* Residuen sind absolute Differenzen zwischen den Werten der realen Stichprobe (Simulationsergebnisse) und den aus der Approximationsfunktion (hier Polynom 2.Ordnung) für den gleichen Punkt berechneten Werten. Die Residuen sind somit ein Maß für die Qualität der Approximation. | * Residuen sind absolute Differenzen zwischen den Werten der realen Stichprobe (Simulationsergebnisse) und den aus der Approximationsfunktion (hier Polynom 2.Ordnung) für den gleichen Punkt berechneten Werten. Die Residuen sind somit ein Maß für die Qualität der Approximation. | ||
* Entscheidend sind nicht die Absolutwerte der Residuen, sondern die relativen Fehler in Bezug auf die Originalwerte der Stützstellen. | * Entscheidend sind nicht die Absolutwerte der Residuen, sondern die relativen Fehler in Bezug auf die Originalwerte der Stützstellen. Wobei natürlich berücksichtigt werden sollte, an welchen Stellen der Ersatzfunktion die größten Fehler auftreten. | ||
* Die größten Fehler treten meist an Stellen stark nichtlinearer Abhängigkeiten auf. Im Beispiel ist dies der Abschaltvorgang, welcher unter ungünstigen Bedingungen zu extremen Spannungsspitzen führen kann. | |||
* Die | |||
[[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_- | Unabhängig von der Größe der Restfehler sollte man überprüfen, ob Polynome höherer Ordnung eine bessere Approximation an den kritischen Stellen erzeugen. Der Aufwand dafür ist gering, wenn die reale Stichprobe hinreichend groß auch für höhere Polynom-Ordnungen war: | ||
'''Die Praegung als Restriktionsgröße''' wurde bewusst nicht in die | * Nach Erhöhung der Polynom-Ordnung von 2 auf 3, sind nicht nur monotone Krümmungen der Ersatzfunktion möglich, sondern auch Wendepunkte sowie lokal steilere Anstiege. | ||
* Auf den ersten Blick scheint es sich um eine ganz normale Verteilungsdichtefunktion zu handeln. | * Im Beispiel genügt die Erhöhung der Ordnung für die bisher in den Diagrammen betrachteten vier Restriktionsgrößen. | ||
* Unter Nutzung der vorhandenen realen Stichprobe kann man auf "Knopfdruck" [[Datei:Software_OptiY_-_Button_-_response_surface_neu.gif|middle]] sofort die Antwortflächen neu berechnen lassen. | |||
* Beispielhaft sollen anhand der Residuen von '''vMax''' die Auswirkungen für die Polynom-Ordnungen 2, 3 und 4 verglichen werden: | |||
'''Polynom-Ordnung 2''':<div align="center">[[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_residual-plot_vmax_ordnung2.gif|.]]</div> | |||
'''Polynom-Ordnung 3''':<div align="center">[[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_residual-plot_vmax_ordnung3.gif|.]]</div> | |||
'''Polynom-Ordnung 4''':<div align="center">[[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_residual-plot_vmax_ordnung4.gif|.]]</div> | |||
* Die Erhöhung der Polynom-Ordnung von 2 auf 3 bringt insbesondere für die "Ausreißer" eine sichtbare Verbesserung. | |||
* Weitere Erhöhungen der Polynom-Ordnung ändern qualitativ wenig, erhöhen jedoch die Gefahr der Überanpassung durch "Welligkeiten". | |||
Im Beispiel sollte man die '''Polynom-Ordnung''' für alle Restriktionsgrößen einheitlich auf den '''Wert=3''' erhöhen, um eine etwas verbesserte Anpassung zu erhalten! Damit alle Ergebnisse des Experiments mit dieser neuen Polynom-Ordnung aktualisiert werden, sind folgende Schritte erforderlich: | |||
# [[Datei:Software_OptiY_-_Button_-_response_surface_neu.gif|middle]] '''''Analyse > Antwortflächen > Neu Berechnen''''' | |||
# [[Datei:Software_OptiY_-_Button_-_sensitivitaet_neu.gif|middle]] '''''Analyse > Sensitivität > Neu Berechnen''''' | |||
# [[Datei:Software_OptiY_-_Button_-_probabilistik_neu.gif|middle]] '''''Analyse > Probabilistik > Neu Berechnen''''' | |||
Wir haben bisher die Qualität der Ersatzfunktion nur auf Grundlage der Residuen bewertet, d.h,, wie gut diese Ausgleichsfunktion die vorhandenen Datenpunkte der Stichprobe trifft: | |||
* Wir werden später noch unterschiedliche Diagramm-Typen behandeln, welche ein Gefühl für das qualitative "Aussehen" der Ersatzfunktionen vermitteln können. | |||
* Hier handelt es sich jeweils um Funktionen im 6-dimensionalen Raum (Funktionen von jeweils 5 variablen Parametern). | |||
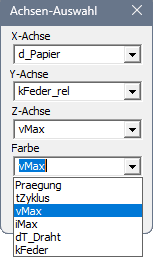
* Am Beispiel von '''vMax''' generieren wir ein 3D-Diagramm, welches nur die 2 einflussreichsten Variablen berücksichtigt (das sind voraussichtlich '''Papierdicke''' und '''Federtoleranz'''). | |||
* '''''Analyse > Antwortflächen > 3D Fläche''''' mit entsprechender Achsenwahl. | |||
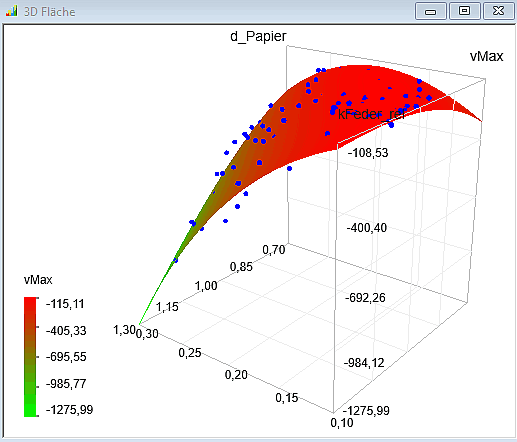
* Das generierte 3D-Diagramm kann man mit gedrückter linker Maustaste frei drehen:<div align="center">[[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_vMax-3D_Flaeche_Achsenwahl.gif|.]] [[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_vMax-3D_Flaeche.gif|.]]</div> | |||
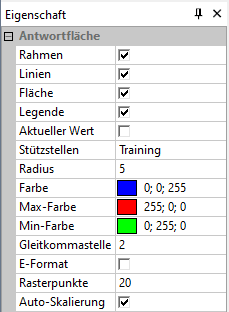
* Nach Klick auf das Diagramm erscheint das zugehörige Eigenschaftsfeld, in dem man zusätzlich als Stützstellen die Trainingsdaten einblenden kann:<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_vMax-3D_Flaeche_Eigenschaft.gif|.]] </div> | |||
* Im 3D-Diagramm erkennt man deutlich, dass der Extremwert der Abschaltspannung aus dem gleichzeitigem Auftreten von dickstem Papier und steifster Rückholfeder resultiert. | |||
* Die berechneten Punkte der realen Stichprobe (Trainingsdaten) liegen nicht exakt auf der Ersatzfunktion. Die sichtbaren Abstände entsprechen jedoch nicht direkt den Werten der Residuen, da es sich um Projektion aus dem 6- in den 3-dimensionalen Raum handelt (der dann noch auf eine 2D-Fläche abgebildet wird). | |||
'''Die Praegung als Restriktionsgröße''' wurde bewusst nicht in die vorherigen Ergebnis-Fenster aufgenommen: | |||
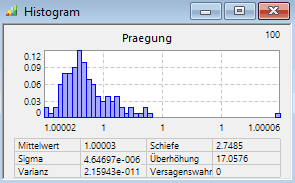
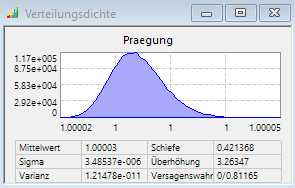
* Auf den ersten Blick scheint es sich um eine ganz normale Verteilungsdichtefunktion zu handeln:<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_histogramm_praegung.gif|.]] </div> | |||
* Beim genaueren Betrachten der statistischen Kenngrößen sieht man, dass hier die numerische Realisierung des plastischen Anschlages als elastisch-dämpfende Ersatzfunktion abgebildet wird. | * Beim genaueren Betrachten der statistischen Kenngrößen sieht man, dass hier die numerische Realisierung des plastischen Anschlages als elastisch-dämpfende Ersatzfunktion abgebildet wird. | ||
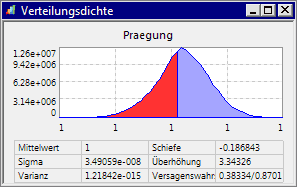
* Der ideale plastische Anschlag würde zu exakt '''Praegung=1''' führen. Die von uns gewählte leichte Nachgiebigkeit für den Anschlag ergibt beim vollständigen Prägen immer Werte etwas größer als 1. Die resultierende "Eindringtiefe" der Nadel in den Anschlag steigt näherungsweise proportional zu deren Aufprall-Impuls. Für die berechneten Stützstellen kann problemlos eine hinreichend genaue Antwortfläche ermittelt werden. | * Der ideale plastische Anschlag würde zu "exakt" '''Praegung=1''' führen. Die von uns gewählte leichte Nachgiebigkeit für den Anschlag ergibt beim vollständigen Prägen immer Werte etwas größer als 1. Die resultierende "Eindringtiefe" der Nadel in den Anschlag steigt näherungsweise proportional zu deren Aufprall-Impuls. Für die berechneten Stützstellen kann problemlos eine hinreichend genaue Antwortfläche ermittelt werden:<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_verteilungsdichte_praegung.gif|.]] </div> | ||
* Die Teilversagenswahrscheinlichkeit der virtuellen Stichprobe infolge "Nichtprägens" ist in unserem Beispiel deshalb Null | * Die Teilversagenswahrscheinlichkeit der virtuellen Stichprobe infolge "Nichtprägens" ist in unserem Beispiel deshalb Null (bei einem eingestellten zulässigen Bereich von z.B. '''1 .. 1,1'''). | ||
'''''Beachte bei "idealen" Anschlägen'':''' | |||
* Würde man (wie in den ersten beiden Etappen) den Anschlag als idealen starren Anschlag realisieren, so wäre der Wert der '''Praegung''' nur in der Größenordnung von 1e-8 größer als 1, wobei es sich hierbei vor allem um ein "Rauschen" der numerischen Lösung handeln würde. | |||
* | * Damit würde im Histogramm immer noch eine Teilversagenswahrscheinlichkeit von Null angezeigt. | ||
* Allerdings ergäbe sich eine mehr oder weniger "zufällige" Antwortfläche über diese verrauschten Abtaststellen. | |||
* Die virtuelle Stichprobe ermittelt dann auf Grund der unzureichenden Antwortfläche für die Prägung eine "zufällige" Teilversagenswahrscheinlichkeit (im gezeigten Beispiel von ca. 40%):<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_verteilungsdichte_praegung_starrer_Anschlag.gif|.]] </div> | |||
* Um damit die berechnete Gesamtversagenswahrscheinlichkeit nicht extrem zu verfälschen, muss man für solche "unrealen" Verteilungsfunktionen die zulässigen Grenzwerte entsprechend anpassen (im Beispiel untere Grenze = 0,999) | |||
'''''===>>> Die folgenden Abschnitte werden noch überarbeitet !!!''''' | |||
=== Versagenswahrscheinlichkeit === | === Versagenswahrscheinlichkeit === | ||
| Zeile 98: | Zeile 150: | ||
Im Normalfall kommt es nach einer Nennwert-Optimierung in mehr als der Hälfte der Einsatzfälle zu einem unzulässigem Lösungsverhalten. Im Beispiel sind es sogar ca. 80%. Das spricht nicht sehr für eine "optimale" Lösung". Da man aber bei einer Nennwert-Optimierung meist einige der zulässigen Grenzwerte ausreizt, ist dieses Ergebnis jedoch typisch! | Im Normalfall kommt es nach einer Nennwert-Optimierung in mehr als der Hälfte der Einsatzfälle zu einem unzulässigem Lösungsverhalten. Im Beispiel sind es sogar ca. 80%. Das spricht nicht sehr für eine "optimale" Lösung". Da man aber bei einer Nennwert-Optimierung meist einige der zulässigen Grenzwerte ausreizt, ist dieses Ergebnis jedoch typisch! | ||
=== DOE-Tabelle === | === DOE-Tabelle === | ||
* DOE=[https://de.wikipedia.org/wiki/Design_of_Experiments '''"Design of Experiments"'''] (Versuchsplanung) | * DOE=[https://de.wikipedia.org/wiki/Design_of_Experiments '''"Design of Experiments"'''] (Versuchsplanung) [[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_doe-tabelle_auswahlliste.gif|right]] | ||
* '''''Analyse > Statistische Versuchsplanung > DOE-Tabelle''''' listet für jede Modellrechnung (=1 Zeile) der realen Stichprobe eine Auswahl der im Workflow definierten Größen auf. | * '''''Analyse > Statistische Versuchsplanung > DOE-Tabelle''''' listet für jede Modellrechnung (=1 Zeile) der realen Stichprobe eine Auswahl der im Workflow definierten Größen auf. | ||
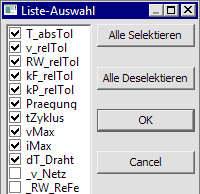
* Die Auswahl erfolgt zuvor über eine Auswahl-Liste:<div align="center">[[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_doe-tabelle.gif| ]]</div> | * Die Auswahl erfolgt zuvor über eine Auswahl-Liste:<div align="center">[[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_doe-tabelle.gif| ]]</div> | ||
| Zeile 146: | Zeile 185: | ||
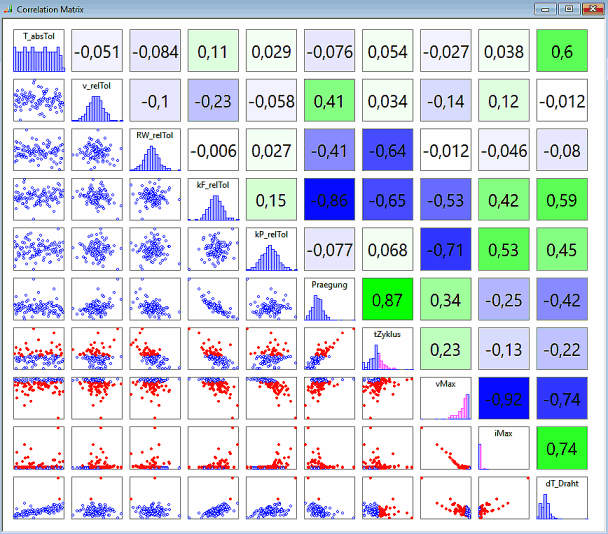
'''''Analyse > Statistische Versuchsplanung > Korrelationsmatrix'':''' | '''''Analyse > Statistische Versuchsplanung > Korrelationsmatrix'':''' | ||
<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_korrelation-matrix.gif| ]] </div> | <div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_korrelation-matrix.gif| ]] </div> | ||
* Der [https://de.wikipedia.org/wiki/Korrelationskoeffizient '''Korrelationskoeffizient'''] '''K''' mit einem Bereich von -1 bis +1 | * Der [https://de.wikipedia.org/wiki/Korrelationskoeffizient '''Korrelationskoeffizient'''] '''K''' mit einem Bereich von -1 bis +1 ist auch farblich gekennzeichnet: | ||
** |K|=0 → keine Korrelation mit der Toleranzgröße | ** |K|=0 → keine Korrelation mit der Toleranzgröße (weiß) | ||
** |K|=1 → starke Korrelation mit der Toleranzgröße. | ** |K|=1 → starke Korrelation mit der Toleranzgröße (dunkelblau). | ||
* '''K''' ist ein dimensionsloses Maß für den Grad des '''''linearen''''' Zusammenhangs zwischen zwei Merkmalen: | * '''K''' ist ein dimensionsloses Maß für den Grad des '''''linearen''''' Zusammenhangs zwischen zwei Merkmalen: | ||
** Korrelationskoeffizienten sind nur gültig, wenn der Zusammenhang zwischen den betrachteten Größen linear ist! | ** Korrelationskoeffizienten sind nur gültig, wenn der Zusammenhang zwischen den betrachteten Größen linear ist! | ||
** Existiert ein nichtlinearer Zusammenhang, so ist der angezeigte Korrelationskoeffizient umso falscher, je stärker die Abweichung von einer Geraden ist. | ** Existiert ein nichtlinearer Zusammenhang, so ist der angezeigte Korrelationskoeffizient umso falscher, je stärker die Abweichung von einer Geraden ist. | ||
** Eine qualitative Abschätzung der Linearität kann man auf Basis der zugehörigen Anthill-Plots vornehmen. Im Beispiel kann man innerhalb des Streubereichs existierende Zusammenhänge zwischen den Größen hinreichend genau durch Ausgleichsgeraden abbilden (das wäre nicht mehr möglich z.B. bei einem zu schwach dimensionierten Antrieb, der teilweise das Papier nicht prägt!). | ** Eine qualitative Abschätzung der Linearität kann man auf Basis der zugehörigen Anthill-Plots vornehmen. Im Beispiel kann man innerhalb des Streubereichs existierende Zusammenhänge zwischen den Größen hinreichend genau durch Ausgleichsgeraden abbilden (das wäre nicht mehr möglich z.B. bei einem zu schwach dimensionierten Antrieb, der teilweise das Papier nicht prägt!). | ||
'''Hinweise zur Interpretation der Korrelationsmatrix:''' | |||
* Entlang der Diagonalen sind die einzelnen Streuungen als Histogramme eingetragen. | |||
* Die 2D-Anthill-Plots unterhalb der Diagonalen stellen den Zusammenhang zwischen jeweils zwei Streuungen dar. | |||
* | * Welche zwei Streuungen dies jeweils sind, ergibt sich durch Verfolgen der Spalte und Zeile bis zur Diagonalen. | ||
* Spiegelbildlich zu den 2D-Anthill-Plots befinden sich oberhalb die zugehörigen Korrelationskoeffizienten. | |||
* | * Falls die Bildung der Zufallszahlen gut funktioniert, darf keine Korrelation zwischen unterschiedlichen Parameter-Streuungen existieren (K=0). Auf Grund der kleinen Stichprobe ist ca. |K|<0.25. Die Korrelation zwischen streuenden Parametern hat insbesondere Bedeutung bei der Benutzung von Messwerten. | ||
*''''' | * Die Korrelation zwischen streuenden Parametern und Bewertungsgrößen ist abhängig vom Übertragungsverhalten des Modells. | ||
*'''''Achtung:''''' Korrelation bedeutet nicht "kausale Abhängigkeit"! In technischen Anwendungen verbergen sich aber dahinter häufig Ursache-Wirkungs-Beziehungen. Man erkennt auf Grund des Absolutwertes der Koeffizienten, in welchem Maße überhaupt ein Zusammenhang zwischen der Änderung zweier Größen bestehen könnte. | |||
* Uns interessieren hier nur die Zusammenhänge zwischen der Streuung der Eingangsgrößen und deren Auswirkung auf die Bewertungsgrößen: | * Uns interessieren hier nur die Zusammenhänge zwischen der Streuung der Eingangsgrößen und deren Auswirkung auf die Bewertungsgrößen: | ||
** Damit können wir uns auf die Auswertung des farblich markierten Viertels der Korrelationstabelle beschränken. | ** Damit können wir uns auf die Auswertung des farblich markierten Viertels der Korrelationstabelle beschränken. | ||
| Zeile 171: | Zeile 211: | ||
'''Widerspiegelung unterschiedlicher Korrelationskoeffizienten im Anthill-Plot:''' | '''Widerspiegelung unterschiedlicher Korrelationskoeffizienten im Anthill-Plot:''' | ||
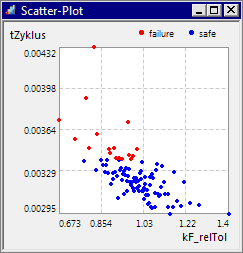
* Eine starke Korrelation besteht im Beispiel zwischen der Zykluszeit und der Federkonstante | * Eine starke Korrelation besteht im Beispiel zwischen der Zykluszeit und der Federkonstante. Die starke Korrelation widerspiegelt sich im Diagramm, indem die Lösungspunkte relativ dicht entlang einer gedachten Ausgleichsgeraden angeordnet sind. | ||
<div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_scatter-plot_t_kf.gif| ]] </div> | <div align="center"> [[Bild:Software_SimX_-_Nadelantrieb_-_Probabilistische_Simulation_-_scatter-plot_t_kf.gif| ]] </div> | ||
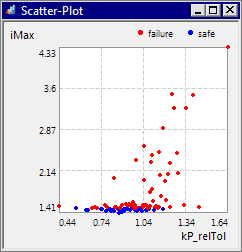
* Der Maximalwert des Stromes korreliert relativ stark mit der Papierfestigkeit. Der Anstieg dieser Ausgleichsgerade ist im Unterschied zum vorherigen Diagramm positiv: | * Der Maximalwert des Stromes korreliert relativ stark mit der Papierfestigkeit. Der Anstieg dieser Ausgleichsgerade ist im Unterschied zum vorherigen Diagramm positiv: | ||
| Zeile 249: | Zeile 289: | ||
# Zwischen welchen Paaren "Streuung/Bewertungsgröße" (ohne Berücksichtigung von "Praegung"!) bestehen die 4 größten Korrelationen? Die zu den Paaren gehörenden Koeffizienten-Werte sind mit anzugeben. | # Zwischen welchen Paaren "Streuung/Bewertungsgröße" (ohne Berücksichtigung von "Praegung"!) bestehen die 4 größten Korrelationen? Die zu den Paaren gehörenden Koeffizienten-Werte sind mit anzugeben. | ||
# Welche 2 Streugrößen kann man auf Grund ihres geringen Effektes auf die Bewertungsgrößen vernachlässigen? Diese Wahl ist zu begründen. | # Welche 2 Streugrößen kann man auf Grund ihres geringen Effektes auf die Bewertungsgrößen vernachlässigen? Diese Wahl ist zu begründen. | ||
<div align="center"> [[Software:_SimX_-_Nadelantrieb_-_Probabilistik_-_Sample-Methoden| | <div align="center"> [[Software:_SimX_-_Nadelantrieb_-_Probabilistik_-_Sample-Methoden|←]] [[Software:_SimX_-_Nadelantrieb_-_Probabilistik_-_Moment-Methoden|→]] </div> | ||
Aktuelle Version vom 10. Mai 2024, 19:48 Uhr
Wichtig: Falls es noch nicht geschehen ist - man muss Simulation als Optimierungsverfahren wählen!
Versuchsplanung
Das "Latin Hypercube Sampling" ist ein geeignetes Zufallsverfahren, um in unserem Beispiel mit akzeptablem Berechnungsaufwand hinreichend genaue und anschauliche Ergebnisse zu erhalten:
- Im OptiY ist das voreingestellte Standard-Verfahren als "Latin Hypercube Sampling" konfiguriert.
- Wählen wir als Verfahren manuell die "Sampling Methode", so werden zusätzlich der standardmäßige Stichproben-Umfang und die Konfiguration des Zufallsgenerator sichtbar:
Leider wird sogar bei dem voreingestellten Standard-Verfahren der Anwender mit einer Vielzahl von Konfigurationsmöglichkeiten konfrontiert, welche nur in speziellen Szenarien erforderlich sind. Wir möchten nur eine Toleranzanalyse für wenige Streuungen auf der Basis von Modellberechnungen durchführen. Deshalb werden im Folgenden alle Eingabefelder minimiert, deren Parameter dafür nicht nötig sind:
Die minimierten (hier nicht benötigten) Eingabefelder konfigurieren folgende Aspekte:
- Trainingsdaten: Auswahlmethode für Menge der Trainingsdaten für das Meta-Modell, wenn nicht alle Modellabtastungen für die Identifikation dieser Ersatzfunktion verwendet werden.
- Kernel-Methode: ermöglicht es durch Transformationen von Datensätzen in höher dimensionale Räume, "ähnliche" Datenpunkte durch lineare Funktionen in Cluster zu separieren (z.B. erforderlich bei Meta-Modellen mit Cluster-Bildung)
- Nichtlineare Methode: wie die Kernel-Methode ein Ansatz des maschinellen Lernens, allerdings mit nichtlinearen Funktionen zur Cluster-Bildung.
- 1D-Variable: 1D-Variable sind spezielle Daten-Elemente, welche anstatt einzelner Werte dynamische Signale in der Form von Y=f(X) enthalten.
- Hierarchische Matrix: Konfiguration der Matrixberechnung auf einen GPU bei großen Datenmengen.
- Robust Design: Konfiguration der probabilistischen Optimierung unter Nutzung des Meta-Modells
Wir werden uns in dieser Übungsetappe auf das Verstehen der Grundlagen der Sample-Methode konzentrieren. Deshalb beschränken wir uns auf Polynom-Funktionen als einfachsten Ansatz für ein Meta-Modell:
- Die minimal erforderliche Anzahl der Modellberechnungen M (=Stichprobenumfang) ergibt sich aus der Anzahl n der stochastischen Variablen und der gewählten Ordnung O der Polynom-Funktion zu M=(n²-n)/2+O*n+1.
- Wir werden für die Ersatzfunktionen Polynome 2. Ordnung benutzen. Damit benötigt man im Beispiel bei 5 Streuungen minimal M=21 Modellberechnungen.
- Da das Polynom 2. Ordnung nicht exakt die wirkliche Übertragungsfunktion im Streubereich nachbildet, muss mittels der Methode der kleinsten Fehlerquadrate eine optimal zu den Datenpunkten passende Ausgleichsfunktion gefunden werden.
- Die Genauigkeit der ermittelten Polynom-Ausgleichsfunktion steigt mit der Anzahl der verfügbaren Datenpunkte.
Konfiguration der "realen" und "virtuellen" Stichprobe:
- Ein Stichprobenumfang=100 für die Gewinnung der "realen" Datensätze ist im Beispiel ein guter Kompromiss zwischen Berechnungsaufwand und Genauigkeit.
- Entscheidend für die Reproduzierbarkeit der Ergebnisse ist die Konfiguration des Zufallszahlengenerators. Dieser produziert nach seiner Initialisierung immer die gleiche Sequenz von Zahlen. Indem man den Zeitpunkt der Initialisierung steuert, kann man unterschiedliche Effekte erzielen:
- Initialisiert
Bewirkt eine Initialisierung mit dem Wert=1 beim Start einer jeden neuen Toleranz-Simulation, d.h. für die Berechnung jeder neuen Stichprobe. Bei gleichen Nennwerten erhält man also bei der Berechnung jeder Stichprobe exakt die gleichen Simulationsergebnisse. - Zeitabhängig initialisiert
Bewirkt eine Initialisierung mit einem Wert=f(Maschinenzeit) beim Start einer jeden neuen Toleranz-Simulation. Damit sind die Ergebnisse auch bei gleichen Nennwerten von Simulation zu Simulation unterschiedlich, weil der Startpunkt des Zufallsgenerators zeitabhängig ist. Dies widerspiegelt sicher am besten die praktisch mögliche Bandbreite von Stichproben-Ergebnissen und wird deshalb gewählt! - Nicht initialisiert
Bewirkt eine einmalige Initialisierung mit dem Wert=1 beim Start des Programms OptiY. Startet man danach ein gespeichertes Experiment, so erzielt man damit immer die gleichen Ergebnisse. Damit lassen sich Toleranzbehaftete Experimente zu unterschiedlichen Zeiten auch auf unterschiedlichen Computern reproduzieren. Da die Zufallszahlen von allen vorhergehenden Vorgängen abhängig sind, erfordert eine Experiment-Reproduktion jedoch immer den vorherigen Neustart von OptiY!
- Initialisiert
- Die gewählte Initialisierungsart für den Zufallszahlengenerator wirkt auch für die "virtuelle" Stichprobe.
- Ein Virtueller Stichprobenumfang=200000 auf der aus der Approximationsfunktion gebildeten Antwortfläche ist ein guter Kompromiss zwischen Berechnungszeit und statistischer Genauigkeit.
- Das Verteilungsraster=50 definiert, wie eckig bzw. geglättet die probabilistischen Ergebnisse grafisch dargestellt werden (z.B. die Verteilungsdichtefunktionen).
Approximationsfunktion:
- Die Auswahl der Approximationsfunktionen ("Antwortflächen") für die Durchführung der virtuellen Stichprobe ist eigentlich Bestandteil der Versuchsplanung.
- Für jede Bewertungsgröße des Modells (Restriktion bzw. Gütekriterium) kann jedoch eine individuelle Approximationsfunktion gewählt werden.
- Deshalb erfolgt für jede Bewertungsgröße getrennt die Wahl der Approximation. Im Beispiel wählen wir für alle Restriktionen einheitlich Polynomiale Approximation mit der Ordnung=2.
- Polynom-Typ = Einheitliche Ordnung bedeutet dabei die Verwendung der gleichen Polynomordnung in Richtung der Koordinatenachse jeder Streuung. Die unterschiedliche Wirkung einer Streuung auf eine Restriktionsgröße könnte man auch durch unterschiedliche Polynomordnungen in jede Streuungsrichtung berücksichtigen.
- Standardmäßig werden alle Parameter (=Streuungen) in die Approximation der Ersatzfunktion einbezogen → im Beispiel:
dT_Draht = f(T_Spule, d_Papier, v_el; Re_Eisen, kFeder_rel)
Hinweis::
- Mit diesem quadratischen Ansatz können auch monotone Krümmungen im betrachteten Bereich des Parameterraumes nachgebildet werden.
- Es muss hier nur der sehr kleine Streubereich um die Toleranzmittenwerte nachgebildet werden. Die globalen Nichtlinearitäten des Originalmodells spielen dabei meist keine Rolle!
Visualisierung und Interpretation
Bei der Nutzung von Sample-Verfahren kann man bereits während der Simulation den Verlauf des Experiments beobachten:
- Dazu bildet man in Histogrammen die interessierenden streuenden Parameter und die daraus berechneten Bewertungsgrößen ab (Analyse > Statistische Versuchsplanung > Histogramme mit anschließendem Drag&Drop der darzustellenden Größen).
- Wie in der Realität wird nach dem Start der Simulation aus der gesamten Stichprobe ein Modell-Exemplar nach dem nächsten untersucht.
- Die generierten Histogramme der streuenden Parameter und die Ergebnisgrößen werden nach jedem einzelnen Simulationslauf aktualisiert.
- Die Ergebnisse der Stichproben-Simulation werden umso genauer, je weiter man innerhalb der Stichprobe voranschreitet.
Streuende Parameter
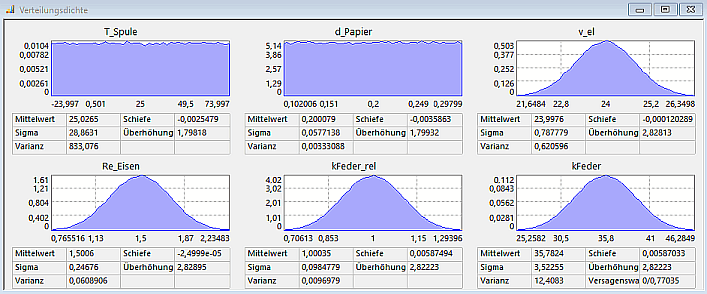
Zusätzlich zu den Streuungen wurde als Ergänzung zur normierten Feder-Toleranz kFeder_rel die daraus berechnete absolute Feder-Toleranz kFeder (Restriktionsgröße ohne Wirkung) als Histogramm abgebildet:
- In den Histogrammen kann man überprüfen, ob die Streuungen sich in den vorgesehenen Grenzen bewegen.
- Dabei muss man beachten, dass es für Normalverteilungen keine festen Grenzen gibt und einige Exemplare der Stichprobe außerhalb der vorgegebenen Grenzen liegen können!
- Im Verlaufe der Berechnung kann man qualitativ beurteilen, ob der "reale" Stichproben-Umfang für eine "saubere" Verteilungsdichte ausreicht.
- In den Histogrammen werden nur die Modellberechnungen der "realen" Stichprobe dargestellt:
Unmittelbar nach der Simulation der "realen" Stichprobe werden die Übertragungsfunktionen (Antwortflächen) der Bewertungsgrößen auf Basis der gewählten Approximationsfunktionen berechnet. Mit diesem Ersatzmodell erfolgt dann die Simulation der "virtuellen" Stichprobe:
- Die Punkte der realen Stichprobe werden bei der Auswertung der virtuellen Stichprobe zusätzlich berücksichtigt. Die darin enthaltene Information geht somit nicht verloren.
- Infolge des extremen Stichprobenumfanges (im Beispiel 200 000) ist es möglich, auch für die streuenden Parameter "geglättete" Verteilungsdichtefunktionen zu generieren.
- Für die Bewertungsgrößen liegen im Ergebnisse der virtuellen Stichprobe ebenfalls die Verteilungsdichtefunktionen vor. Somit können wir jetzt auch die absolute Verteilungsdichte der Federsteife darstellen.
- In Analogie zu den Histogrammen öffnen wir alle zugehörigen Verteilungsdichte-Darstellungen ( Analyse > Probabilistik > Verteilungsdichte ):
- Bei den statistischen Kenngrößen gibt es Abweichungen zwischen der realen und der virtuellen Stichprobe. Die Größe der Abweichungen wird im Wesentlichen durch den Umfang der realen Stichprobe bestimmt. Letztendlich bestimmt diese das Vertrauensintervall der statistischen Aussagen!
Hinweis: Im OptiY werden Ersatzfunktionen (Antwortflächen) nur für die Bewertungsgrößen approximiert. Für alle anderen Ergebnisgrößen (z.B. Ausgangsgrößen) des Experiment-Workflows stehen nur die Werte der "realen" Stichprobe zur Verfügung. Deren Streuung kann man in Histogrammen darstellen.
Restriktionen
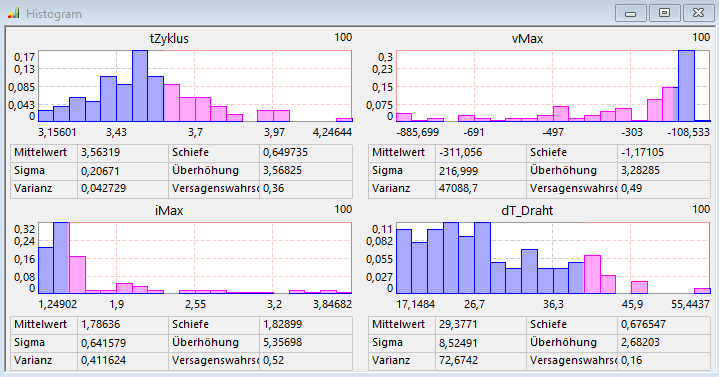
Man erkennt in den entsprechenden Histogrammen schon während der Stichproben-Berechnung, in welchem Maße Restriktionen verletzt werden. Kritisch sind im Beispiel die Abschaltspannungen, welche im Beispiel über 800 V erreichen und wahrscheinlich zusammen mit Stromspitzen von ca. 4 A auftreten:
Histogramm-Eigenschaften:
- Man kann mehrere Histogramme in einem Histogramm-Fenster darstellen.
- Die X-Achse ist standardmäßig in 50 Bereiche (Balken) aufgeteilt.
- Die Höhe der Balken repräsentiert auf der Y-Achse die anteilige Häufigkeit der Stichprobenpunkte im jeweiligen Intervall.
- Weitere Informationen wie Mittelwert, Schiefe, Überhöhung, Varianz und Standardabweichung stehen zur Verfügung.
- Bei Restriktionen wird auch die Teil-Versagenswahrscheinlichkeit bezüglich der dargestellten Restriktionsgröße angezeigt.
- Bereiche mit Restriktionsverletzungen werden markiert.
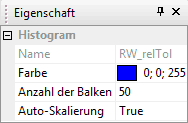
Wählt man mit dem Cursor ein Histogramm aus, so erscheinen die Histogramm-Eigenschaften im Eigenschaftsfenster:
- Die Eigenschaften beziehen sich auf alle Histogramme des gewählten Histogramm-Fensters, auch wenn der Name eines konkreten Histogramms angezeigt wird.
- Man kann die Anzahl der Balken verändern. Wählt man Dichte als Y-Achse=Falsch, so wird die Anzahl der im einzelnen Balken enthaltenen Stichproben-Exemplare angezeigt.
- Die Grenzen der X-Achse werden standardmäßig durch Auto-Skalierung=Wahr ermittelt. Wählt man Auto-Skalierung=Falsch, so kann man die Grenzen (Min, Max) für das gewählte Histogramm manuell einstellen.
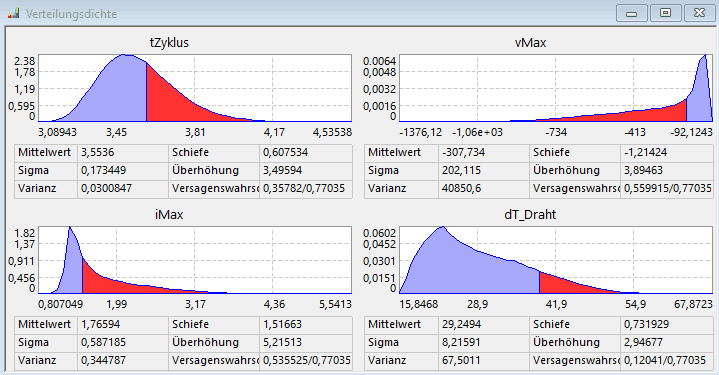
Auch bei den Verteilungsdichten der Restriktionen sind Bereiche mit unzulässigen Werten markiert. So erhält man einen qualitativen Eindruck, in welchem Maße Restriktionen verletzt werden. Zusätzlich steht der Wert der Teilversagenswahrscheinlichkeit unterhalb der Grafik zusammen mit der Gesamtversagenswahrscheinlichkeit:
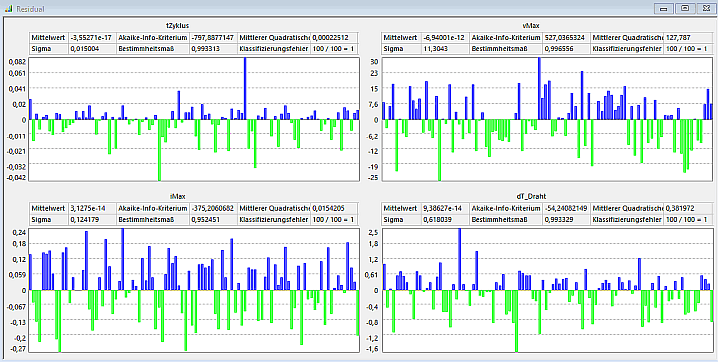
Wie exakt die Approximationsfunktionen der Ausgangsgrößen an die Punkte der realen Stichprobe angepasst wurden, kann man mittels der Residual-Diagramme überprüfen (Analyse > Antwortflächen > Residuum Plot - Drag&Drop der Restriktionen/Gütekriterien):
- Residuen sind absolute Differenzen zwischen den Werten der realen Stichprobe (Simulationsergebnisse) und den aus der Approximationsfunktion (hier Polynom 2.Ordnung) für den gleichen Punkt berechneten Werten. Die Residuen sind somit ein Maß für die Qualität der Approximation.
- Entscheidend sind nicht die Absolutwerte der Residuen, sondern die relativen Fehler in Bezug auf die Originalwerte der Stützstellen. Wobei natürlich berücksichtigt werden sollte, an welchen Stellen der Ersatzfunktion die größten Fehler auftreten.
- Die größten Fehler treten meist an Stellen stark nichtlinearer Abhängigkeiten auf. Im Beispiel ist dies der Abschaltvorgang, welcher unter ungünstigen Bedingungen zu extremen Spannungsspitzen führen kann.
Unabhängig von der Größe der Restfehler sollte man überprüfen, ob Polynome höherer Ordnung eine bessere Approximation an den kritischen Stellen erzeugen. Der Aufwand dafür ist gering, wenn die reale Stichprobe hinreichend groß auch für höhere Polynom-Ordnungen war:
- Nach Erhöhung der Polynom-Ordnung von 2 auf 3, sind nicht nur monotone Krümmungen der Ersatzfunktion möglich, sondern auch Wendepunkte sowie lokal steilere Anstiege.
- Im Beispiel genügt die Erhöhung der Ordnung für die bisher in den Diagrammen betrachteten vier Restriktionsgrößen.
- Unter Nutzung der vorhandenen realen Stichprobe kann man auf "Knopfdruck"
 sofort die Antwortflächen neu berechnen lassen.
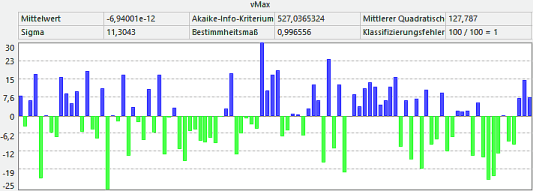
sofort die Antwortflächen neu berechnen lassen. - Beispielhaft sollen anhand der Residuen von vMax die Auswirkungen für die Polynom-Ordnungen 2, 3 und 4 verglichen werden:
Polynom-Ordnung 2:
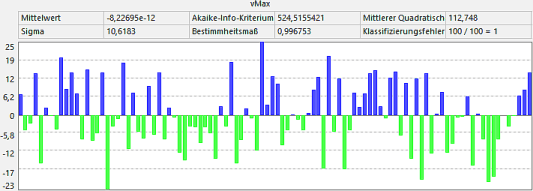
Polynom-Ordnung 3:
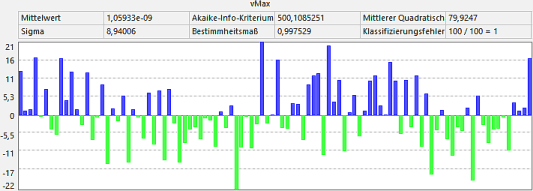
Polynom-Ordnung 4:
- Die Erhöhung der Polynom-Ordnung von 2 auf 3 bringt insbesondere für die "Ausreißer" eine sichtbare Verbesserung.
- Weitere Erhöhungen der Polynom-Ordnung ändern qualitativ wenig, erhöhen jedoch die Gefahr der Überanpassung durch "Welligkeiten".
Im Beispiel sollte man die Polynom-Ordnung für alle Restriktionsgrößen einheitlich auf den Wert=3 erhöhen, um eine etwas verbesserte Anpassung zu erhalten! Damit alle Ergebnisse des Experiments mit dieser neuen Polynom-Ordnung aktualisiert werden, sind folgende Schritte erforderlich:
 Analyse > Antwortflächen > Neu Berechnen
Analyse > Antwortflächen > Neu Berechnen Analyse > Sensitivität > Neu Berechnen
Analyse > Sensitivität > Neu Berechnen Analyse > Probabilistik > Neu Berechnen
Analyse > Probabilistik > Neu Berechnen
Wir haben bisher die Qualität der Ersatzfunktion nur auf Grundlage der Residuen bewertet, d.h,, wie gut diese Ausgleichsfunktion die vorhandenen Datenpunkte der Stichprobe trifft:
- Wir werden später noch unterschiedliche Diagramm-Typen behandeln, welche ein Gefühl für das qualitative "Aussehen" der Ersatzfunktionen vermitteln können.
- Hier handelt es sich jeweils um Funktionen im 6-dimensionalen Raum (Funktionen von jeweils 5 variablen Parametern).
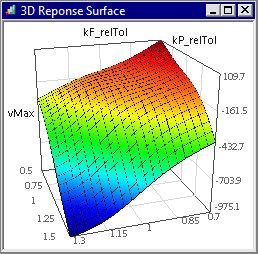
- Am Beispiel von vMax generieren wir ein 3D-Diagramm, welches nur die 2 einflussreichsten Variablen berücksichtigt (das sind voraussichtlich Papierdicke und Federtoleranz).
- Analyse > Antwortflächen > 3D Fläche mit entsprechender Achsenwahl.
- Das generierte 3D-Diagramm kann man mit gedrückter linker Maustaste frei drehen:
- Nach Klick auf das Diagramm erscheint das zugehörige Eigenschaftsfeld, in dem man zusätzlich als Stützstellen die Trainingsdaten einblenden kann:
- Im 3D-Diagramm erkennt man deutlich, dass der Extremwert der Abschaltspannung aus dem gleichzeitigem Auftreten von dickstem Papier und steifster Rückholfeder resultiert.
- Die berechneten Punkte der realen Stichprobe (Trainingsdaten) liegen nicht exakt auf der Ersatzfunktion. Die sichtbaren Abstände entsprechen jedoch nicht direkt den Werten der Residuen, da es sich um Projektion aus dem 6- in den 3-dimensionalen Raum handelt (der dann noch auf eine 2D-Fläche abgebildet wird).
Die Praegung als Restriktionsgröße wurde bewusst nicht in die vorherigen Ergebnis-Fenster aufgenommen:
- Auf den ersten Blick scheint es sich um eine ganz normale Verteilungsdichtefunktion zu handeln:
- Beim genaueren Betrachten der statistischen Kenngrößen sieht man, dass hier die numerische Realisierung des plastischen Anschlages als elastisch-dämpfende Ersatzfunktion abgebildet wird.
- Der ideale plastische Anschlag würde zu "exakt" Praegung=1 führen. Die von uns gewählte leichte Nachgiebigkeit für den Anschlag ergibt beim vollständigen Prägen immer Werte etwas größer als 1. Die resultierende "Eindringtiefe" der Nadel in den Anschlag steigt näherungsweise proportional zu deren Aufprall-Impuls. Für die berechneten Stützstellen kann problemlos eine hinreichend genaue Antwortfläche ermittelt werden:
- Die Teilversagenswahrscheinlichkeit der virtuellen Stichprobe infolge "Nichtprägens" ist in unserem Beispiel deshalb Null (bei einem eingestellten zulässigen Bereich von z.B. 1 .. 1,1).
Beachte bei "idealen" Anschlägen:
- Würde man (wie in den ersten beiden Etappen) den Anschlag als idealen starren Anschlag realisieren, so wäre der Wert der Praegung nur in der Größenordnung von 1e-8 größer als 1, wobei es sich hierbei vor allem um ein "Rauschen" der numerischen Lösung handeln würde.
- Damit würde im Histogramm immer noch eine Teilversagenswahrscheinlichkeit von Null angezeigt.
- Allerdings ergäbe sich eine mehr oder weniger "zufällige" Antwortfläche über diese verrauschten Abtaststellen.
- Die virtuelle Stichprobe ermittelt dann auf Grund der unzureichenden Antwortfläche für die Prägung eine "zufällige" Teilversagenswahrscheinlichkeit (im gezeigten Beispiel von ca. 40%):
- Um damit die berechnete Gesamtversagenswahrscheinlichkeit nicht extrem zu verfälschen, muss man für solche "unrealen" Verteilungsfunktionen die zulässigen Grenzwerte entsprechend anpassen (im Beispiel untere Grenze = 0,999)
===>>> Die folgenden Abschnitte werden noch überarbeitet !!!
Versagenswahrscheinlichkeit
Die Teilversagenswahrscheinlichkeiten der einzelnen Restriktionsgrößen sagen nur etwas über die Größenordnung der gesamten Versagenswahrscheinlichkeit aus:
- Die Gesamtversagenswahrscheinlichkeit (Ausschussquote) ist mindestens so groß wie die größte Teilversagenswahrscheinlichkeit.
- Sie ist kleiner als die Summe aller Teilversagenswahrscheinlichkeiten, da sich deren Bereiche überlappen. Die Gesamtversagenswahrscheinlichkeit wird im OptiY-Explorer als Bestandteil der Gütekriterien aufgelistet, besitzt jedoch kein Eigenschaftsfeld:
- Ihr Wert wird nach erst nach Abschluss der probabilistischen Simulation (einschließlich der virtuellen Stichprobe) berechnet.
- Den Wert der Versagenswahrscheinlichkeit kann man sich in einem Nennwert-Verlauf-Fenster anzeigen lassen. Dazu muss man die Versagenswahrscheinlichkeit per Drag&Drop in den grafischen Ausgabe-Bereich von OptiY ziehen.
Im Normalfall kommt es nach einer Nennwert-Optimierung in mehr als der Hälfte der Einsatzfälle zu einem unzulässigem Lösungsverhalten. Im Beispiel sind es sogar ca. 80%. Das spricht nicht sehr für eine "optimale" Lösung". Da man aber bei einer Nennwert-Optimierung meist einige der zulässigen Grenzwerte ausreizt, ist dieses Ergebnis jedoch typisch!
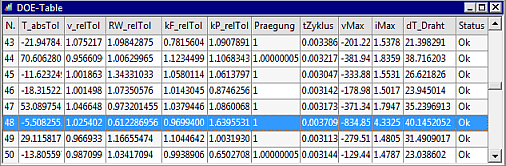
DOE-Tabelle
- DOE="Design of Experiments" (Versuchsplanung)
- Analyse > Statistische Versuchsplanung > DOE-Tabelle listet für jede Modellrechnung (=1 Zeile) der realen Stichprobe eine Auswahl der im Workflow definierten Größen auf.
- Die Auswahl erfolgt zuvor über eine Auswahl-Liste:
- Die in der Tabelle markierte Zeile zeigt, dass hier eine hohe Abschaltspannung von 835 V in Kombination mit einem steifen Papier kP_relTol=1.65 und einem hohem Maximalstrom von 4.33 A auftritt.
- Wenn man innerhalb dieser Tabelle eine Zeile mit Doppelklick auswählt (= Exemplar der realen Stichprobe), so wird der zugehörige Punkt in den im Folgenden beschriebenen Anthill-Plots hervorgehoben und es werden dort auch die "Koordinatenwerte" eingeblendet.
- Über die Menü-Funktion Datei > Daten Export kann man die Datensätze der DOE-Tabelle bei Bedarf zur Weiterverarbeitung in eine Excel-Tabelle speichern (Achtung: in der DOE-Tabelle zuvor eine Zeile mit Klick der linken Maustaste auswählen!)
Anthill-Plot
Der "Ameisenhaufen" stand Pate für die Bezeichnung dieser Darstellform (Punktdiagramm), welche auch als Streudiagramm (engl. Scatterplot) bekannt ist. In OptiY existieren zwei Formen von Anthill-Plots. In beiden Formen werden nur Punkte der realen Stichprobe eingetragen:
Analyse > Cluster > 2D-Anthill-Plot:
- Die X- und Y-Achse sind frei belegbar mit den im Workflow definierten Größen.
- Jedes Exemplar der realen Stichprobe wird durch einen Punkt repräsentiert, der den Zusammenhang zwischen den beiden gewählten Größen verdeutlicht.
- Sind Achsen mit Restriktionen belegt, so werden die Punkte mit unzulässigen Werten rot markiert:
Im Beispiel erkennt man "Ausreißer" mit extremen Spannungswerten von bis zu 835 V:
- Sucht man den zugehörigen Simulationslauf in der DOE-Tabelle, so erkennt man, dass diese hohe Abschaltspannung aus einem Maximalstrom von 4.33 A resultiert.
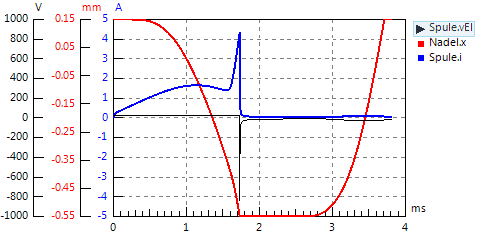
- Startet man den zugehörigen Simulationslauf, so sieht man, dass es sich nicht um ein numerisches Problem bei der Modellberechnung handelt:
- Es entsteht kurz vor dem Abschalten eine Stromspitze, weil das Eisenmaterial infolge "unglücklicher" Umstände in die Sättigung gelangt. Solch ein "Ausreißer" muss also ernst genommen werden!
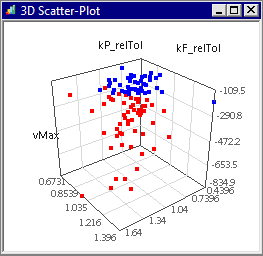
Analyse > Cluster > 3D-Anthill-Plot:
- Es besteht auch die Möglichkeit, die Abhängigkeit einer Ergebnis-Größe (z.B. der Abschaltspannung) von zwei Streu-Größen darzustellen (z.B. Papiersteife und Federkonstante):
- Die X-, Y- und Z-Achse dieses 3D-Scatter-Plots sind frei belegbar mit den im Workflow definierten Größen.
- Auch in diesem Diagramm wird die reale Stichprobe als Punktwolke dargestellt.
- Im Beispiel erkennt man, dass Kombinationen von steiferem Papier und steiferer Feder zu einer höheren Abschaltspannung tendieren. Das würde man auf Grund von Vorüberlegungen auch erwarten.
Korrelationen
Es wird die Korrelation zwischen allen Streuungen und Restriktionen/Gütekriterien in Form von Korrelationskoeffizienten dargestellt. Im OptiY gibt es zwei Möglichkeiten der Darstellung:
Analyse > Statistische Versuchsplanung > Korrelationsmatrix:
- Der Korrelationskoeffizient K mit einem Bereich von -1 bis +1 ist auch farblich gekennzeichnet:
- |K|=0 → keine Korrelation mit der Toleranzgröße (weiß)
- |K|=1 → starke Korrelation mit der Toleranzgröße (dunkelblau).
- K ist ein dimensionsloses Maß für den Grad des linearen Zusammenhangs zwischen zwei Merkmalen:
- Korrelationskoeffizienten sind nur gültig, wenn der Zusammenhang zwischen den betrachteten Größen linear ist!
- Existiert ein nichtlinearer Zusammenhang, so ist der angezeigte Korrelationskoeffizient umso falscher, je stärker die Abweichung von einer Geraden ist.
- Eine qualitative Abschätzung der Linearität kann man auf Basis der zugehörigen Anthill-Plots vornehmen. Im Beispiel kann man innerhalb des Streubereichs existierende Zusammenhänge zwischen den Größen hinreichend genau durch Ausgleichsgeraden abbilden (das wäre nicht mehr möglich z.B. bei einem zu schwach dimensionierten Antrieb, der teilweise das Papier nicht prägt!).
Hinweise zur Interpretation der Korrelationsmatrix:
- Entlang der Diagonalen sind die einzelnen Streuungen als Histogramme eingetragen.
- Die 2D-Anthill-Plots unterhalb der Diagonalen stellen den Zusammenhang zwischen jeweils zwei Streuungen dar.
- Welche zwei Streuungen dies jeweils sind, ergibt sich durch Verfolgen der Spalte und Zeile bis zur Diagonalen.
- Spiegelbildlich zu den 2D-Anthill-Plots befinden sich oberhalb die zugehörigen Korrelationskoeffizienten.
- Falls die Bildung der Zufallszahlen gut funktioniert, darf keine Korrelation zwischen unterschiedlichen Parameter-Streuungen existieren (K=0). Auf Grund der kleinen Stichprobe ist ca. |K|<0.25. Die Korrelation zwischen streuenden Parametern hat insbesondere Bedeutung bei der Benutzung von Messwerten.
- Die Korrelation zwischen streuenden Parametern und Bewertungsgrößen ist abhängig vom Übertragungsverhalten des Modells.
- Achtung: Korrelation bedeutet nicht "kausale Abhängigkeit"! In technischen Anwendungen verbergen sich aber dahinter häufig Ursache-Wirkungs-Beziehungen. Man erkennt auf Grund des Absolutwertes der Koeffizienten, in welchem Maße überhaupt ein Zusammenhang zwischen der Änderung zweier Größen bestehen könnte.
- Uns interessieren hier nur die Zusammenhänge zwischen der Streuung der Eingangsgrößen und deren Auswirkung auf die Bewertungsgrößen:
- Damit können wir uns auf die Auswertung des farblich markierten Viertels der Korrelationstabelle beschränken.
- Betrachtet man nacheinander die einzelnen Toleranzgrößen, so kann man folgende Schlussfolgerungen ziehen:
- Temperatur des Spulendrahtes: korreliert am stärksten mit dessen Erwärmung (anscheinend, weil sich der ohmsche Widerstand des Drahtes linear mit der Temperatur ändert).
- Betriebsspannung: korreliert kaum mit den Bewertungsgrößen (anscheinend nur geringer Einfluss oder kein linearer Zusammenhang).
- Wirbelstroms: korreliert stark mit der Zykluszeit (je größer der Wirbelstrom, desto stärker die Abfallverzögerung - deshalb negativer Koeffizient!).
- Federkonstante: korreliert stark mit der Zykluszeit (negativer Wert bedeutet, dass eine härtere Feder die Zykluszeit verkleinert), korreliert aber auch relativ stark mit allen anderen Bewertungsgrößen.
- Papiersteife: korreliert sehr stark mit der Abschaltspannung und dem maximalem Spulenstrom (härteres Papier könnte also die Ursache für zu hohe Abschaltspannungen sein?).
- Hinweis zur Praegung: Infolge der Verwendung eines elastisch-dämpfenden Ansatzes zur Nachbildung des ideal plastischen Stoßes wird in Abhängigkeit vom Aufschlag-Impuls eine entsprechende Eindringtiefe berechnet. Diese Eindringtiefe korreliert dann relativ stark mit allen Eingangsgrößen, welche den Aufschlag-Impuls beeinflussen. Die größte Korrelation besteht zur Federsteife (steifere Federn könnten also den Prägungsvorgang am stärksten negativ beeinflussen). Bei Verwendung des starren Anschlags würden die Korrelationen nur das nummerische Rauschen um den Idealwert=1 abbilden und wäre praktisch wertlos!
Widerspiegelung unterschiedlicher Korrelationskoeffizienten im Anthill-Plot:
- Eine starke Korrelation besteht im Beispiel zwischen der Zykluszeit und der Federkonstante. Die starke Korrelation widerspiegelt sich im Diagramm, indem die Lösungspunkte relativ dicht entlang einer gedachten Ausgleichsgeraden angeordnet sind.
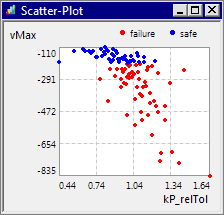
- Der Maximalwert des Stromes korreliert relativ stark mit der Papierfestigkeit. Der Anstieg dieser Ausgleichsgerade ist im Unterschied zum vorherigen Diagramm positiv:
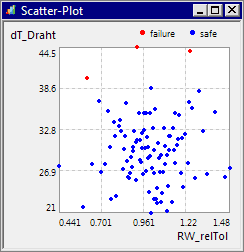
- Kleine Korrelationskoeffizienten werden durch eine ausgedehnte Punktwolke repräsentiert (z.B. zwischen dem Wirbelstrom und der Drahterwärmung). Der Wert der Restriktionsgröße wird dann überwiegend von den anderen Streugrößen bestimmt!
Sensitivitäten
Auch wenn eine Ausgangsgröße sehr stark mit einer Eingangsgröße korreliert, kann der tatsächliche Einfluss dieser Eingangsgröße auf den Wert der Ausgangsgröße sehr gering sein! Deshalb ist das Erkennen von Korrelationen nur der erste Schritt, um diejenigen Eingangsgrößen zu finden, welche praktisch mit keiner Ausgangsgröße korrelieren. Im Beispiel scheint die Spulentemperatur solch eine "einflusslose" Eingangsgröße zu sein. Sie korreliert zwar mit der Erwärmung der Spule, diese Erwärmung (äußert sich wieder in der Spulentemperatur) wird aber die anderen Bewertungsgrößen kaum beeinflussen.
Den tatsächlichen Einfluss einer Streugröße erkennt man erst im Ergebnis einer Sensitivitätsanalyse. Dabei kann man zwei Arten von Sensitivitäten unterscheiden.
Lokale Sensitivität
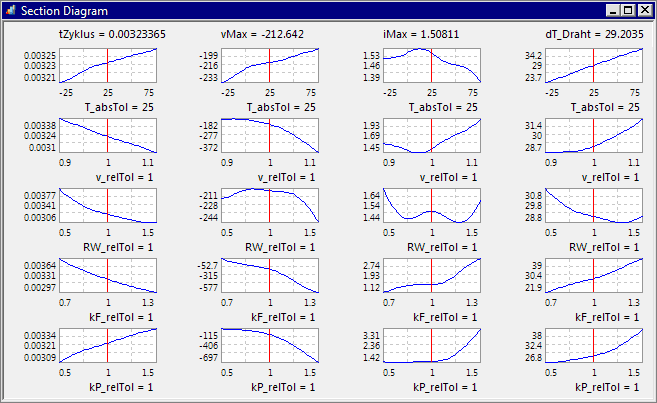
Bei einer lokalen Sensitivitätsanalyse wird jeweils ein Parameter verändert. Alle anderen Parameter bleiben dabei konstant (Siehe "c.p." = ceteris paribus). In OptiY wird dafür das Schnittdiagramm bereitgestellt (Analyse > Antwortflächen > Schnittdiagramm):
- Die Abhängigkeiten der Bewertungsgrößen (Restriktionen/Gütekriterien) von den Streuungen werden als Kurven dargestellt.
- Die gewünschten Elemente muss man per Drag&Drop aus dem OptiY-Explorer in das anfangs leere Diagrammfenster ziehen:
- Hinweis: Je nach gewählter Approximationsfunktion können sich die konkreten Schnittverläufe insbesondere bei kleinen Funktionswert-Änderungen (auf der Y-Achse) stark unterscheiden. Beim Verwenden des Gauß-Prozesses können zusätzlich einzelne Störstellen (z.B. durch numerisches "Rauschen" infolge gestörter Ereignisbehandlungen bei Schaltvorgängen) als Peaks auf ansonsten stetigen Kurven abgebildet werden!
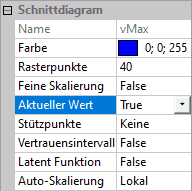
- Die Kurven-Verläufe gelten jeweils für die aktuellen Istwerte aller Streuungen. Diese werden im Schnittdiagramm als senkrechte Linien eingeblendet, wenn man dies in den Eigenschaften des Schnittdiagramms aktiviert:
- Die zu den Istwerten gehörigen Werte der Bewertungsgrößen sind als Zahlenwerte eingeblendet.
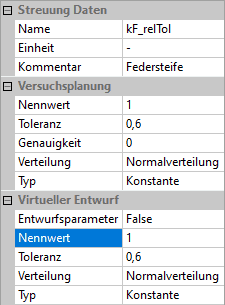
- Die Istwerte kann man im Eigenschaftsfenster der Streuungen verändern. Dazu selektiert man die entsprechende Streuung im Explorer, dort existiert im Eigenschaftsfenster unter der Rubrik Virtueller Entwurf der Eintrag Nennwert. Dabei handelt es sich um den "aktuellen Istwert" der Streuungsgröße auf dem "virtuellen" Ersatzmodell. Nach der Eingabe eines neuen "Ist"-Wertes werden alle Schnittdiagramme automatisch aktualisiert.
- Prinzipiell kann man in den Schnittdiagrammen die roten Istwert-Linien auch mit der Maus verschieben. Damit ist jedoch nur ein grober qualitativer Eindruck möglich.
Lokale Sensitivität SL (Definition):
- Partielle Ableitung der Approximationsfunktion einer Bewertungsgröße nach einer Streugröße im eingestellten Arbeitspunkt (Istwert).
- Entspricht dem Anstieg der linearisierten Schnittfunktion im Arbeitspunkt.
- Ist ein Maß dafür, wie empfindlich eine Bewertungsgröße auf die Änderung der betrachteten Streugröße reagiert.
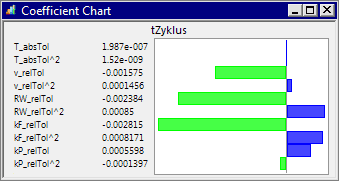
Lokale Sensitivitäten kann man direkt aus dem Koeffizienten-Chart (Analyse > Antwortflächen > Koeffizient-Chart) ablesen, welches die Parameter des Polynom-Anteils der Approximationsfunktion enthält (X: partielle Ableitung 1. Ordnung, X^2: partielle Ableitung 2. Ordnung, X1*X2: partielle Kreuzableitung usw.):
- Die Ableitung 1. Ordnung entspricht der mittleren lokalen Sensitivität im betrachteten Toleranzbereich.
- Dies soll am gleichen Beispiel der lokale Sensitivität SL der Zykluszeit in Hinblick auf die Streuung der Federkonstante demonstriert werden. Dazu öffnet man den Koeffizient-Chart für tZyklus.
- kF_relTol=−0.002815 ist die partielle Ableitung erster Ordnung, allerdings nach der relativen Toleranzgröße.
Hinweis:
In obigen Schnittdiagrammen wird der Einfluss einer Streugröße auf jeweils eine Bewertungsgröße dargestellt. Die in OptiY bereitgestellten 3D-Antwortflächen berücksichtigen den Einfluss von zwei Streugrößen auf jeweils eine Bewertungsgröße. Diese Erweiterung des Schnittdiagramms kann im Spezialfall für die Anschauung nützlich sein. Auch die 3D-Antwortflächen werden bei der Änderung von Istwerten der Streugrößen aktualisiert. Im Folgenden sieht man die Analogie zum zuvor abgebildeten 3D-Anthill-Plot (Abschaltspannung in Abhängigkeit von Papier- und Federsteife):
Globale Sensitivitäten
Mit der Sensibilitätsanalyse auf Basis der Schnittdiagramme ermittelten wir die lokalen Sensitivitäten als partielle Ableitung 1. Ordnung gemittelt über das jeweilige Streuintervall. Wie empfindlich das Systemverhalten auf die Änderung einer Streugröße reagiert, sagt noch nichts über den Einfluss einer Streuung im Vergleich zum Einfluss der anderen Streugrößen. Dafür muss man die sogenannte "globale Sensitivität" betrachten:
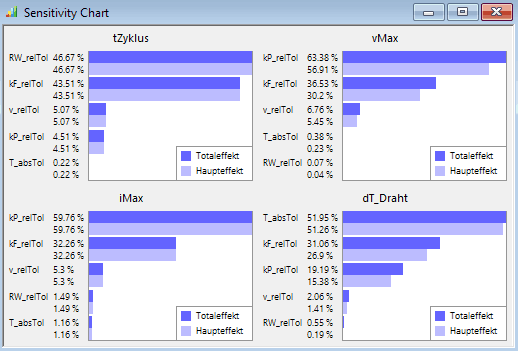
- Wir wollen uns zuerst die zugehörigen Ergebnisse anschauen (Analyse > Sensitivität > Sensitivität-Chart). Es erscheint zuerst ein leeres Fenster, in das man die gewünschten Bewertungsgrößen (Restriktionen und Gütekriterien) per Drag&Drop aus dem Explorer hineinziehen kann. Für jede dieser Bewertungsgrößen wird dann ein Sensitivität-Chart (Pareto-Chart) in Bezug auf alle Streuungen generiert:
- Unter Pareto-Chart versteht man ein Balkendiagramm (Histogramm), das anzeigt, in welchem Maße ein bestimmtes Ergebnis (Effekt) durch eine bestimmte Ursache (Streuung) hervorgerufen wurde. Die Balken sind nach der Größe des Effektes geordnet.
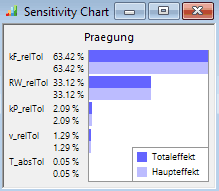
- Hinweis: Die Sensitivitäten der Praegung wurden in einem separatem Fenster dargestellt, weil diese vor allem die Eigenschaften des verwendeten Modellansatzes für den mechanischen Anschlag widerspiegeln!
Den Sensitivität-Charts kann man zwei wesentliche Informationen entnehmen:
- 1. Welche Streuungen haben einen vernachlässigbaren Einfluss auf die betrachteten Bewertungsgrößen?
- Im Beispiel existiert keine Streuung, welche auf sämtliche Bewertungsgrößen keinen Einfluss hat.
- Die Streuung der Spulentemperatur hat nur Einfluss auf die Langzeit-Erwärmung der Spule. Das hatten wir bei der Nennwert-Optimierung bereits durch Annahme des Worst Case "Maximaltemperatur" berücksichtigt! Deshalb werden wir für die weiteren Untersuchungen die Streuung der Spulentemperatur vernachlässigen.
- Der Wirbelstrom hat zwar nur Auswirkung auf die Zykluszeit. Da diese für uns jedoch ein sehr wichtiges Kriterium darstellt, sollte man die Wirbelstrom-Streuung im Folgenden nicht vernachlässigen.
- Kleiner als 10% ist der Einfluss von Schwankungen der Betriebsspannung auf die Streuung aller Bewertungsgrößen. Deshalb kann man die Streuung der Betriebsspannung praktisch vernachlässigen.
- Damit kann man bei einer anschließenden probabilistischen Optimierung den Simulationsaufwand durch Reduktion der zu berücksichtigenden Streuungen von 5 auf 3 entscheidend verringern.
- 2. Existieren merkliche Interaktionen zwischen den Streuungen?
- Es gibt Wechselwirkungen zwischen den Streugrößen, wenn die aktuellen Ist-Werte anderer Streugrößen den Einfluss der jeweils betrachteten Streugröße auf das Systemverhalten merklich verändern.
- In den Sensitivität-Charts erkennt man das an einem merklichem Unterschied zwischen den Werten von Total- und Haupteffekt:
Haupteffekt:
- Er repräsentiert den Haupteinfluss der betrachteten Streugröße Xi auf die Ausgangsgröße Y. Definiert ist er als Quotient aus der Varianz der durch Xi verursachten Streuung der Ausgangsgröße Var(Y|Xi) und der Varianz der durch alle Toleranzen X verursachten Streuung Var(Y|X)
Totaleffekt:
- Er setzt sich zusammen aus dem Haupteffekt und den Interaktionen zwischen den einzelnen Streugrößen (Xi, Xj)
- In OptiY wird die Interaktion durch paarweise Kombination aller Streugrößen berücksichtigt, da die gleichzeitige Berücksichtigung sämtlicher Streugrößen zu einem nicht beherrschbaren Berechnungsaufwand führt. Jedes Paar (Xi, Xj) wird als ein Glied dieser Summenformel berücksichtigt. Der Wert dieses Gliedes ist jeweils Null, wenn es keine Interaktion innerhalb des Streugrößen-Paares gibt.
- Sind Interaktionen zwischen den Streugrößen vernachlässigbar, so hat dies insbesondere Bedeutung für die im folgenden Abschnitt beschriebenen Moment-Methoden. Man kann dann mit vereinfachten Funktionsansätzen arbeiten, welche einen geringeren Berechnungsaufwand erfordern.
Globale Sensitivität SG (Definition):
- Quantifiziert (in %) die anteilige Wirkung einer Streugröße Xi auf die Streuung einer Ausgangsgröße Y.
- Haupteffekt SH: Berücksichtigt nur die direkte Wirkung von Xi auf die Streuung von Y.
- Totaleffekt ST: Berücksichtigt auch die indirekte Wirkung von Xi auf die Streuung von Y infolge der Änderung des Einflusses der anderen Streugrößen Xj.
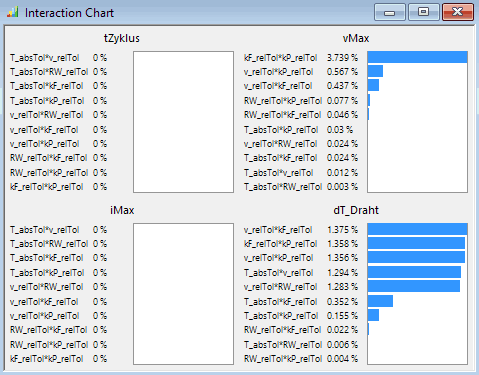
Im Interaction-Chart wird für die ausgewählten Bewertungsgrößen nur der Anteil der indirekten Wirkungen geordnet nach der Größe des hervorgerufenen Effektes dargestellt:
Hinweis:
- Die Größe der berechneten Interaktionen zwischen den Streuungen ist stark abhängig von der Genauigkeit der approximierten Antwortflächen.
- Die Interaktion=0 für iMax und tZyklus wurde im Beispiel nur bei Benutzung des Gauß-Prozesses ermittelt. Bei Verwendung von Polynomen ergeben sich stattdessen Werte bis z.B. ca. 10%!
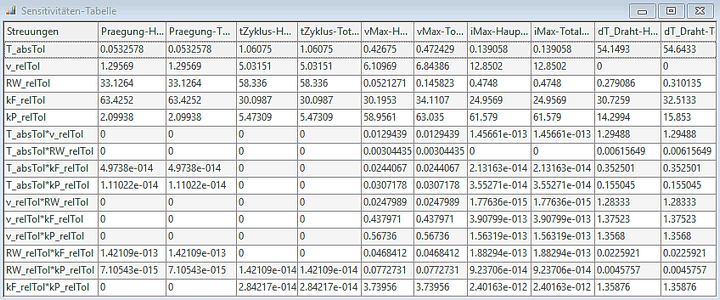
Die komplette Übersicht über alle Abhängigkeiten zwischen den Toleranzen und den Bewertungsgrößen erhält man über die Anzeige der Sensitivitäten-Tabelle. Darin sind für jede Bewertungsgröße jeweils die Werte des Haupt- und des Totaleffekts in Bezug zu jeder Toleranzgröße aufgelistet:
Experiment-Ergebnisse
Für das eigene Nennwert-Optimum sind von den Teilnehmern der Lehrveranstaltung mit der Latin-Hypercube-Simulation folgende Fragen als Bestandteil der einzusendenden Lösung zu beantworten:
- Zwischen welchen Paaren "Streuung/Bewertungsgröße" (ohne Berücksichtigung von "Praegung"!) bestehen die 4 größten Korrelationen? Die zu den Paaren gehörenden Koeffizienten-Werte sind mit anzugeben.
- Welche 2 Streugrößen kann man auf Grund ihres geringen Effektes auf die Bewertungsgrößen vernachlässigen? Diese Wahl ist zu begründen.