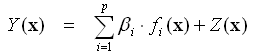Software: FEM - Tutorial - Magnetfeld - Probabilistik - Kennfeld-Identifikation: Unterschied zwischen den Versionen
K (Syntax geändert) |
|||
| Zeile 98: | Zeile 98: | ||
* Die Vertrauensintervalle markieren den ''Worst Case'' der Unsicherheit bei fehlenden Kenntnissen zu den abgebildeten physikalischen Zusammenhängen. | * Die Vertrauensintervalle markieren den ''Worst Case'' der Unsicherheit bei fehlenden Kenntnissen zu den abgebildeten physikalischen Zusammenhängen. | ||
Um ein Gefühl für die Wirkung der Polynomordnung und der unterschiedlichen Covarianz-Funktionen auf die Qualität der Antwortflächen zu erhalten, werden diese Parameter im Folgenden systematisch | Um ein Gefühl für die Wirkung der Polynomordnung und der unterschiedlichen Covarianz-Funktionen auf die Qualität der Antwortflächen zu erhalten, werden diese Parameter im Folgenden systematisch verändert: | ||
Version vom 9. Juli 2010, 10:30 Uhr
Die Kraft- und Koppelfluss-Kennfelder eines E-Magneten kann man in Modellen der System-Simulation als Ersatzmodell für eine konkrete Wandler-Geometrie benutzen:
- Die Ergebnisse einer FEM-Rastersuche kann man als Daten exportieren und die berechneten Abtaststellen des FEM-Modells als Stützstellen von 3D-Funktionsflächen in der System-Simulation verwenden. Aus diesen Stützstellen werden in der System-Simulation dann die Funktionswerte der Zwischenräume interpoliert.
- Die für die Durchführung der virtuellen Stichprobe von OptiY generierten mathematischen Funktionen der Antwortflächen kann man aber auch direkt als Modell-Code in Modelle der System-Simulation implementieren. Die Gewinnung von Ersatzmodellen nach diesem Prinzip wollen wir abschließend in diesem Übungskomplex durchführen.
Ausgehend vom Raster-Experiment Kennfeld-Berechnung konfigurieren wir nach dem Duplizieren ein Experiment Kennfeld-Identifikation.
Workflow
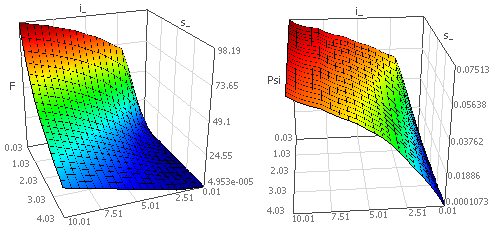
Wir werden die probabilistische Simulation benutzen, um über den gesamten Arbeitsbereich unseres E-Magneten die Antwortflächen für F(i,s) und Psi(i,s) bilden zu lassen:
- Die Nennwerte von Strom und Arbeitsluftspalt sind nun konstante Größen. Diese Streuungsmittenwerte sind so zu wählen, dass über den gesamten Streubereich numerisch instabile Werte nahe Null vermieden werden:
- i.Wert=5.01 A (i≥0.01 A)
- s.Wert=2.03 mm (s≥30 µm)
- Die Streuungen von Strom und Arbeitsluftspalt umfassen den gesamten Arbeitsbereich des E-Magneten:
- #i.Toleranz=10 A
- #s.Toleranz= 4 mm
- #i.Nennwert und #s.Nennwert Null (Streuungsmittenabstand=0)
- Die Gleichverteilung innerhalb der Streu-Bereiche gewährleistet eine gleichmäßige Abtastung, falls man eine Sample Methode verwendet.
Versuchsplanung
Wir werden das Experiment so konfigurieren, dass wir möglichst anschaulich erkennen, wie genau die approximierten Antwortflächen die wirklichen Übertragungsfunktionen des Modells abbilden:
- Grundlage für die Berechnung der Antwortfläche soll das Full Factorial Design sein, welches praktisch einer Rastersuche entspricht. Wir wählen dafür 6 Stufen, um die Anzahl der Modellberechnungen mit 37 gering zu halten. Die Anzahl 37 ergibt sich aus dem Raster 6x6 plus einer Stützstelle in der Mitte.
- Wir setzen den virtuellen Stichprobenumfang=0, da wir in diesem Experiment nur die Antwortflächen gewinnen.
Approximation mit Polynom-Ansatz
- Wir verwenden zuerst die bereits für die Sample Methode genutzte polynomiale Approximation und beginnen mit der Polynomordnung=1.
- Nach Abschluss der Simulation liegen die Antwortflächen als Funktionen im (i,s)-Raum vor.
- In die Diagramme der 3D-Antwortflächen blenden wir die Punkte der berechneten Stützstellen ein.
- Schrittweises Erhöhen der Polynomordnung mit anschließendem Neuberechnen der Antwortflächen
 führt zu einer optimalen Anpassung der Antwortflächen. Aus einem zu großem Wert für die Polynomordnung resultiert dann wieder eine Verschlechterung der Approximation, z.B. durch starke Welligkeit der Fläche.
führt zu einer optimalen Anpassung der Antwortflächen. Aus einem zu großem Wert für die Polynomordnung resultiert dann wieder eine Verschlechterung der Approximation, z.B. durch starke Welligkeit der Fläche.
Achtung: Ein Rücksetzen des Experiments mit erneuter Berechnung der realen Stichprobe ist dabei nicht erforderlich!
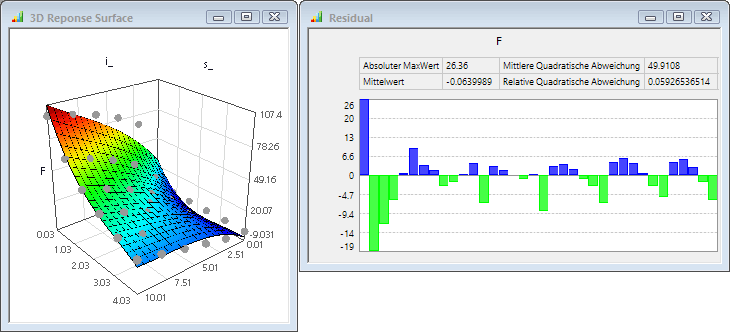
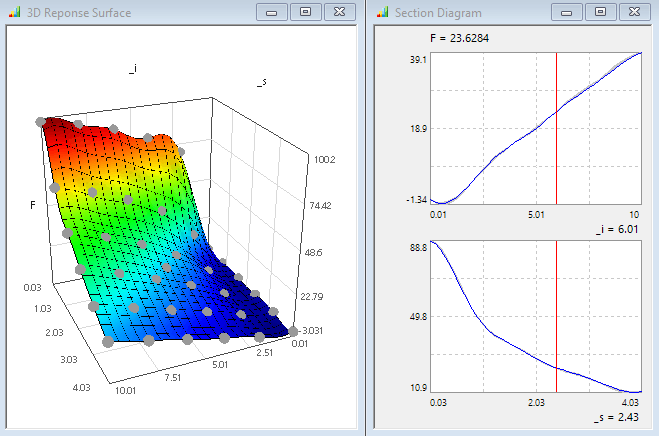
- Ein Drehen des Diagramms der 3D-Antwortfläche zeigt deutlich die Lage der realen Modellwerte abseits der Antwortfläche. Besonders stark sind die Abweichungen bei der Kombination von minimalem Luftspalt mit minimalem Strom.
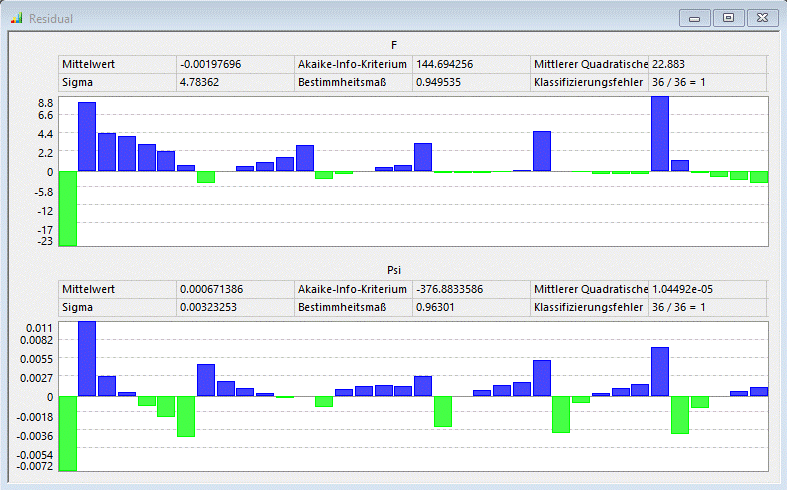
- Das Residuum-Plot zeigt quantitativ die Abbweichungen der realen Modellberechnungen von den identifizierten Antwortflächen. Bei der Magnetkraft liegt diese Abweichung überwiegend im Bereich von ca. 10%, was für ein Ersatzmodell häufig noch akzeptiert werden kann.
- Nicht akzeptabel ist jedoch, dass die Ersatzfunktion im Bereich kleiner Ströme zu negativen Kraftwerten führt, was physikalisch nicht korrekt ist!
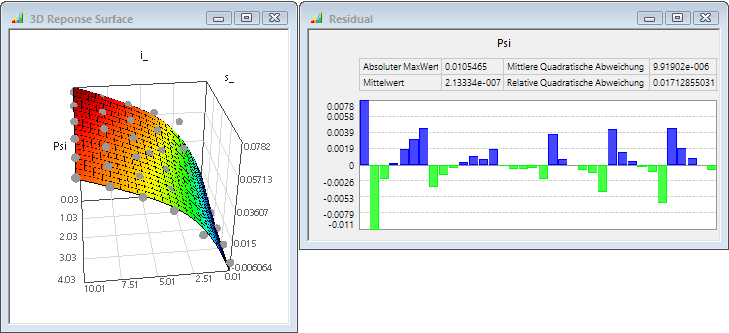
- Ähnlich ungenau sehen die Ergebnisse für das Psi-Kennfeld aus:
Schlussfolgerung:
Polynom-Ansätze sind für die Bildung von globalen Ersatzmodellen bei nichtlinearem Übertragungsverhalten nicht besonders gut geeignet.
Approximation mit Gauss-Prozess
Der Gauss-Prozess, angewandt in der Geostatistik auch als Kriging bekannt, ist ein statistisches Verfahren, mit dem man Werte an Orten, für die keine Probe vorliegt, durch umliegende Messwerte interpolieren oder auch annähern kann.
Der Gauss Prozess besteht aus einem globalen Modell f(x) und einem stochastischen Prozess Z(x), welcher die mögliche Abweichung von dem globalen Modell beschreibt:
- x ist ein m-dimensionaler Parametervektor.
- Y(x) ist der Ergebnisvektor für den Punkt x im Parameterraum.
- f(x) sind Polynome beliebiger Ordnung, welche zusammen mit den unbekannten Regressionskoeffizienten βi die Regressionsfunktion bilden.
- Z(x) ist ein stationärer stochastischer Prozess mit dem Mittelwert Null, der Varianz σ und der Covarianz R. Dieser Anteil des Gauss Prozesses beschreibt das 95% Erwartungsintervall für jeden Punkt x des Parameterraumes.
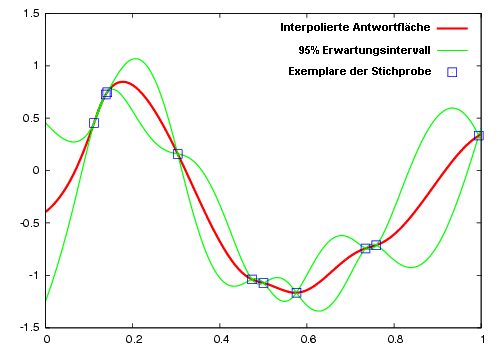
In dem englischen Wikipedia-Artikel zum Kriging wird das für die Interpolation einer eindimensionale Funktion sehr anschaulich dargestellt:
Die berechneten Grenzverläufe des Erwartungsintervalls werden wesentlich bestimmt durch das Erfahrungswissen in Hinblick auf den erwartenden Verlauf der zu interpolierenden Funktion zwischen den bekannten Werten der Stichproben-Exemplare. Diese Erwartung wird durch die Wahl einer geeigneten Covarianz-Funktion R beschrieben.
- In OptiY sind unterschiedlichste Covarianz-Funktionen R iplementiert. Diese beschreiben den Verlauf des 95% Erwartungsintervalls zwischen den Stützstellen in Abhängigkeit von der Stützstellendichte. Die folgende Notation bezieht sich auf zwei Stützstellen x1 und x2 im Abstand (x1−x2):
- Square Exponential
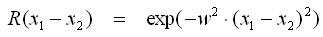
- Exponential
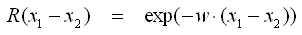
- Gamma-Exponential
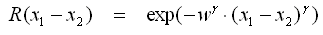
- Matern Class 3/2
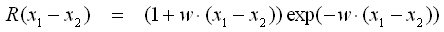
- Matern Class 5/2
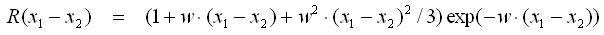
- Rational Quadratic
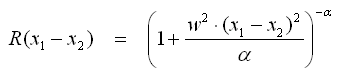
- Der allgemeine Fall für Exponential-Funktionen ist Gamma-Exponential, die anderen beiden Exponentialfunktionen sind die Spezialfälle für γ=1 bzw. γ=2.
- Die Matern Class Funktionen sind Erweiterungen der Exponential-Funktion.
- Die Hyper-Parameter w, γ and α werden mittels der Maximierung der Likelihood-Funktion der multivariaten Normalverteilung ermittelt.
Über die Polynomordnung des globalen Modells kann man einen Kompromiss finden zwischen bester Anpassung der interpolierten Regressionsfunktion an vorhandene Stützstellen und optimalem Verlauf zwischen diesen Stützstellen:
- Wie im vorherigen Abschnitt "Approximation mit Polynom-Ansatz" beschrieben, bestimmt die Polynomordnung des globalen Modells f(x) die allgemeine Richtung (globale Anpassung) der Regressionsfunktion. Die dabei verbleibenden Residuen sind noch sehr groß.
- Der stochastische Prozess Z(x) hat dann die Aufgabe, diese verbleibenden Residuen mittels der Covarianz-Funktion (Normal-Verteilung) zu eliminieren (lokale Anpassung).
- Wenn die Anzahl der Stützstellen bzw. der Daten hinreichend groß ist und man die verbleibenden Residuen statistisch auswertet, entsteht eine Normal-Verteilung (auch Gauss-Verteilung genannt) mit dem Mittelwert=0. Das ist die ursprüngliche Idee des Gauss-Prozesses.
- Wenn man die globale Anpassung mit einer zu hohen Ordnungen der Polynome durchführt, besitzt die Kurve mehr Freiheitsgrade als nötig. Das führt dann zu Welligkeiten zwischen den Stützstellen, weil dies durch keine Zwangsbedingungen verhindert wird.
Dieses Prinzip der Bildung von Ersatzmodellen (Antwortflächen) werden wir nun auf unser Kennfeld-Problem anwenden. Wir nutzen dafür das bereits konfigurierte Experiment Kennfeld-Identifikation ohne erneute Berechnung der Stichprobe:
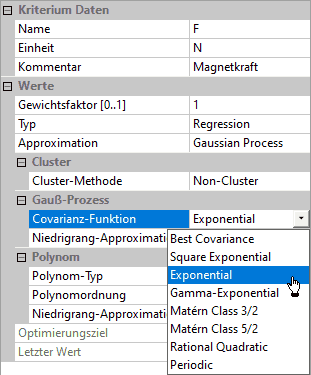
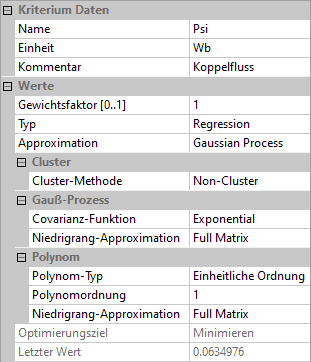
- Wir wählen für die beiden Ergebnisgrößen F und Psi zur Approximation den Gauss Prozess und beginnen mit der kleinsten Polynomordnung=0. Als Covarianz-Funktion beginnen wir mit Exponential:
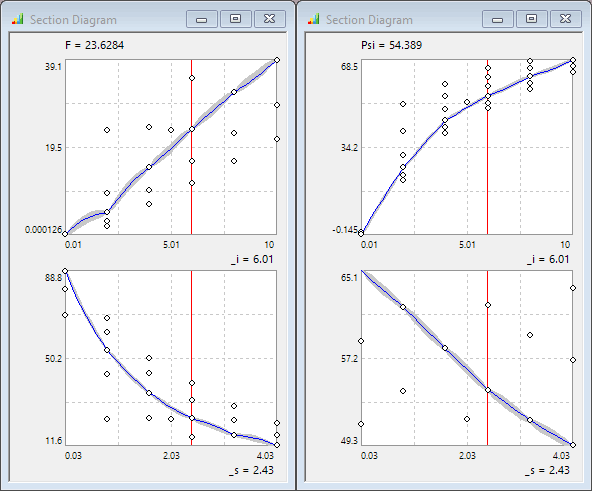
- Zusätzlich zu den Residuen und der 3D-Antwortfläche öffnen wir für jede Ergebnisgröße auch die Schnittdiagramm. Innerhalb der Schnittdiagramme aktivieren wir die Darstellung des Vertrauenintervalls.
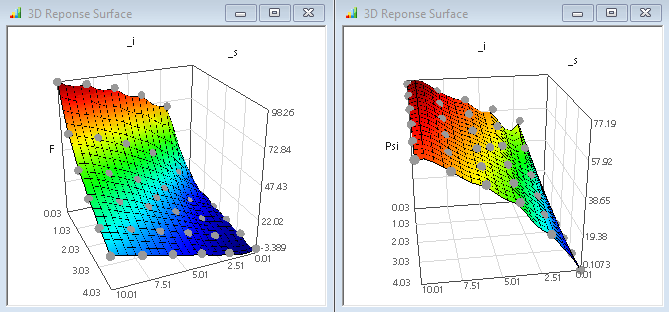
- Nach dem Neuberechnen der Antwortflächen
 ergibt sich eine gute Approximation für beide Kennfelder:
ergibt sich eine gute Approximation für beide Kennfelder: - Positiv fällt auf, dass im Unterschied zum Polynom-Ansatz:
- physikalisch korrekt keine negativen Kräfte oder Koppelflüsse berechnet werden!
- die Residuen zeigen, dass sämtliche Punkte der echten Stichprobe exakt (max. 2E-13) in die identifizierte Ersatzfunktionen F=f(s,i) bzw. Psi=f(s,i) eingebettet sind:
- Negativ fällt auf, dass:
- die identifizierten Kennfelder auf Grund der Polynomordnung=0 für die globale Anpassung schwache Knicke an den Stützstellen besitzen. Hier würde man physikalisch eine stetige Ableitung der Kennfelder erwarten.
- die 95% Vertrauensintervalle zwischen den Stützstellen mit ca. ±20% des Maximalwertes "riesig" sind:
Insbesondere den Aspekt des Vertrauensintervalls wollen wir näher betrachten:
- Um die obige Darstellung der Vertrauensintervalle zu erhalten, müssen wir:
- die Anzeige der Stützpunkte für die Schnittdiagramme aktivieren.
- die aktuellen Werte der Streugrößen auf eine Stützstellen-Reihe setzen (z.B. #i=6.01 A und #s=2.03 mm).
- An den Stützstellen selbst ist die Breite des Vertrauensintervalls immer Null, da der Wert bekannt ist.
Hinweis:
- Die berechneten Vertrauensintervalle resultieren nur aus den benutzten mathematischen Ansätzen. Am Beispiel können wir dem interpolierten Kraftverlauf wesentlich stärker vertrauen! Wir wissen (im Unterschied zum mathematischen Formalismus), dass sich die Kraft zwischen den Stützstellen monoton ändert (ohne "Welligkeit").
- Die Vertrauensintervalle markieren den Worst Case der Unsicherheit bei fehlenden Kenntnissen zu den abgebildeten physikalischen Zusammenhängen.
Um ein Gefühl für die Wirkung der Polynomordnung und der unterschiedlichen Covarianz-Funktionen auf die Qualität der Antwortflächen zu erhalten, werden diese Parameter im Folgenden systematisch verändert:
1. Polynomordnung
- Wir erhöhen die Polynomordnung für beide Ergebnisgrößen schrittweise um 1.
- Nach dem Neuberechnen der Antwortflächen
 ergibt sich im Beispiel eine Verschlechterung des Ersatzmodells in Hinblick auf das physikalische Verständnis:
ergibt sich im Beispiel eine Verschlechterung des Ersatzmodells in Hinblick auf das physikalische Verständnis:
- Für die Magnetkraft entstehen wie beim Polynomansatz negative Werte.
- Die Welligkeit beider Anwortflächen nimmt mit steigender Ordnungszahl zu.
Man sollte die kleinste Polynomordnung verwenden, welche zu physikalisch plausiblen Ersatzmodellen führt! Das wird meist die Polynomordnung=0 sein.
2. Covarianz-Funktion
Wir setzen die Polynomordnung auf den mit dem einfachen Exponential-Ansatz ermittelten optimalen Wert, bevor wir mit den unterschiedlichen Covarianz-Funktionen experimentieren:
- Höherwertige Covarianz-Funktionen führen bei unseren monotonen, stetigen Kennfeldern zu minderwertigen Ergebnissen im Vergleich zum einfachen Exponential-Ansatz:
- Es wird zwar ein schmaleres Vertrauensintervall berechnet, was aber nicht mit dem physikalischen Verständnis des Magnetmodells korreliert!
- Die Kennfelder erhalten eine verstärkte Welligkeit, welche z.B. bei der Magnetkraft zu physikalisch sinnlosen negativen Kraftwerten führen kann.
- Je komplizierter die gewählte Covarianz-Funktion ist, desto größer ist die Wahrscheinlichkeit, dass die globale Approximation für den Gauss-Prozess misslingt:
- Die Identifikation der Parameter für die optimale globale und lokale Anpassung erfolgt mittels numerischer Optimierung. Besitzt die Zielfunktion infolge ihrer Komplexität viele lokale Extremwerte, wird unter Umständen das globale Optimum nicht gefunden.
- Im Beispiel führt die Covarianz-Funktion Matern Class 5/2 für das Psi-Kennfeld bei Polynomordnung=0 zu obiger unsinniger Lösung.
- Erst eine Erhöhung auf Polynomordnung=2 führt mit dieser Covarianz-Funktion zu einer Kennfeld-Qualität, die wir bereits mit Polynomordnung=0 und einfachem Exponential-Ansatz erreichten:
- Das enge 95% Vertrauensintervall bei diesem komplexeren Ersatzmodell hat auch hier keine Bedeutung in Hinblick auf die physikalische Korrektheit der identifizierten Antwortfläche!
Export des Ersatzmodells
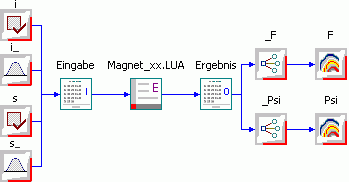
Unabhängig davon, nach welchem Verfahren die Antwortflächen des Modells approximiert wurden, kann man die identifizierten mathematischen Funktionen als Programm-Code exportieren (Analyse - Antwortflächen - Modell Export):
- Zur Zeit kann in OptiY ein Quelltext als C-Code, Modelica-Code oder als m-Matlab erzeugt werden.
- Wir speichern unser Ersatzmodell als C-Code in die Datei Magnet_xx.c. (xx=Teilnehmer-Nummer in der Lehrveranstaltung).
- Dieser Quelltext enthält unter Benutzung der gewählten Covariance-Funktion die identifizierten Gauss-Ketten für alle Kriterien/Restriktionen (im Folgenden gekürzt):
double Covar_F(double x1[],double x2[],double p[])
{
double Co, W;
W = 0;
for(int i = 0; i<2; i++) {
W = W + fabs((x1[i]-x2[i])*p[i]);
}
Co = exp(-W);
return Co;
}
double F(double #i, double #s)
{
double p[2];
double x1[2];
double x2[2];
double y = 29.6033584;
p[0] = 0.0953874971;
p[1] = 0.639066599;
x1[0] = #i;
x1[1] = #s;
x2[0] = 5.01;
x2[1] = 2.03;
y = y-3.56544484*Covar_F(x1,x2,p);
x2[0] = 0.01;
x2[1] = 0.03;
y = y-234.552394*Covar_F(x1,x2,p);
x2[0] = 2.01;
x2[1] = 0.03;
y = y+232.803719*Covar_F(x1,x2,p);
:
:
x2[0] = 10.01;
x2[1] = 4.03;
y = y-1.36321395*Covar_F(x1,x2,p);
return y;
}
double Covar_Psi(double x1[],double x2[],double p[])
{
double Co, W;
W = 0;
for(int i = 0; i<2; i++) {
W = W + fabs((x1[i]-x2[i])*p[i]);
}
Co = exp(-W);
return Co;
}
double Psi(double #i, double #s)
{
double p[2];
double x1[2];
double x2[2];
double y = 0.0426131121;
p[0] = 0.332335577;
p[1] = 0.640793101;
x1[0] = #i;
x1[1] = #s;
x2[0] = 5.01;
x2[1] = 2.03;
y = y+0.0020486711*Covar_Psi(x1,x2,p);
x2[0] = 0.01;
x2[1] = 0.03;
y = y-0.0457279401*Covar_Psi(x1,x2,p);
x2[0] = 2.01;
x2[1] = 0.03;
y = y+0.0346149278*Covar_Psi(x1,x2,p);
:
:
x2[0] = 10.01;
x2[1] = 4.03;
y = y+0.0100595855*Covar_Psi(x1,x2,p);
return y;
}
Hinweise
Die beschriebene Vorgehensweise für die Identifikation von Ersatzmodellen als Antwortflächen mittels Gauss-Prozess ist nur unter den folgenden Randbedingungen durchführbar:
- Es existieren bereits hinreichend viele Stützstellen für das zu identifizierende Modell innerhalb des vorgesehenen Wertebereiches der freien Parameter.
- Die Anzahl der freien Parameter ist überschaubar (z.B. maximal drei).
- Man besitzt bereits qualitative Vorstellungen zu den Eigenschaften der Antwortflächen.
Trifft dies nicht zu, muss man angepasste Strategien verwenden, um mit erträglichem Aufwand hinreichend genaue Ersatzmodelle zu identifizieren. Die Nutzung des adaptiven Gausss-Prozesses zur Beschränkung der Stützstellen auf das unbedingt notwendige Maß wird in einem separaten Übungskomplex des FEM-Tutorials beschrieben.
Qualität der Ableitung:
- Benötigt man innerhalb der Systemsimulation partielle Ableitungen der identifizierten Funktionen, so muss man dies als zusätzliches Qualitätsmerkmal berücksichtigen. Im Beispiel trifft dies für psi(i,s) zu, denn die zeitliche Ableitung des Koppelflusses entspricht im Netzwerkmodell der induzierten Spannung in der Spule.
- Leider kann man die Qualität partieller Ableitungen der indentifizierten Antwortflächen innerhalb des OptiY nur sehr grob beurteilen:
- Knicke bewirken Sprünge der Ableitung
- Welligkeit kann zu Vorzeichenwechsel der Ableitung führen
- Um die physikalische Sinnfälligkeit der Ableitung zu beurteilen, muss man zur Zeit diese Ableitung auf Basis des exportierten Modell-Codes berechnen und Darstellen!