Software: CAD - Tutorial - Optimierung - Probabilistik

↑

← →

Probabilistische Simulation

Nennwert-Simulation:
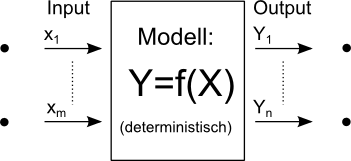
CAD-Modelle benutzen konkrete Werte als Parameter. Die berechneten Ergebnisse entsprechen demzufolge einem Ist-Zustand des modellierten Objektes. Man spricht auch von deterministischer Simulation:

Probabilistische Simulation:
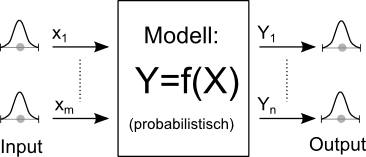
Diese Art der Simulation bietet die Möglichkeit, Streuungen physikalisch-technischer Größen in Form von Verteilungsdichtefunktionen zu berücksichtigen. Die Simulation erfolgt nicht mehr mit "konkreten" Werten, sondern berücksichtigt die Streuung der Werte:

• Wir betrachten damit nicht nur ein konkretes Exemplar des modellierten Objekts unter konkreten Betriebsbedingungen.
• Es wird praktisch eine Stichprobe von allen möglichen Exemplaren und Betriebsbedingungen simuliert.
• Die Ergebnisse dieser Simulation erlauben Aussagen zu statistischen Eigenschaften des modellierten Objekts.
• Grundlage der probabilistischen Simulation ist die statistische Versuchsplanung.

Statistische Versuchsplanung (Design of Experiments DoE):
ermittelt mit möglichst wenigen deterministischen Simulationen (= minimaler "realer" Stichprobenumfang) den Wirkzusammenhang zwischen Einflussfaktoren (= unabhängige Inputgrößen) und Zielgrößen (= abhängige Outputgrößen) hinreichend genau. Damit bildet die statistische Versuchsplanung die Grundlage der probabilistischen Simulation:

• Methoden der statistischen Versuchsplanung unterscheiden sich darin, wie die Stichproben gebildet werden und wie daraus die Berechnung der statistischen Eigenschaften der Zielgrößen erfolgt.
• Streuungen der Inputgrößen beschreiben unabhängig von der verwendeten DoE-Methode die Häufigkeitverteilung innerhalb der Toleranzgrenzen.

Normalverteilung:

• Verteilungen, die durch Überlagerung einer großen Zahl von unabhängigen Einflüssen entstehen, sind annähernd normalverteilt.
• Die Abweichungen der (Mess)Werte vieler natur-, wirtschafts- und ingenieurswissenschaftlicher Vorgänge vom Mittelwert lassen sich deshalb durch die Normalverteilung in sehr guter Näherung beschreiben.
• Dies gilt in unserem Beispiel sowohl für die Abmessungen als auch für den E-Modul der Biegefeder.

Toleranz:

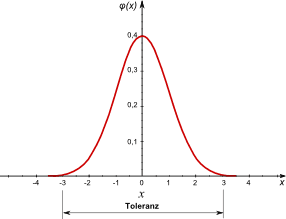
• In der Technik bezeichnet die Toleranz das Intervall der Abweichung ±3σ vom Mittelwert und enthält damit 99,73% aller möglichen Werte.
• Hinweise:
  • Das bedeutet, dass ca. 0,3% aller Istwerte einer normalverteilten Streuung außerhalb der Toleranzgrenzen liegen!
  • Trotz normal-verteilter Fertigungstoleranzen können in der Realität bei ausreichender Qualitätskontrolle keine Maße außerhalb der Toleranzgrenzen vorkommen.
  • Um daraus resultierende Fehler bei der Toleranz-Analyse zu vermeiden, ist es sinnvoll, die Normalverteilung von Maßtoleranzen in solch einem Fall als allgemeine Lampda-Verteilung zu parametrisieren.
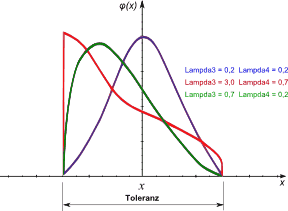
  • Bei diesem Verteilungstyp liegen alle möglichen Istwerte innerhalb der Toleranzgrenzen:
    
  • Mittels der Lambda-Parameter kann man innerhalb der Toleranzgrenzen unter anderem auch die Form der Normalverteilung nachbilden (blaue Kurve).

← →