Software: CAD - Tutorial - Optimierung - Lokale Suche
Bei der globalen Suche haben wir den Einfluss unterschiedlicher Feder-Dicken aufgrund mangelnder Anschaulichkeit und langer Rechenzeiten nicht berücksichtigt. Dies werden wir jetzt bei Anwendung eines lokalen Suchverfahrens nachholen:
- Die lokale Suche beginnt bei einer Ausgangslösung.
- Sie bewegt sich im Lösungsraum zielgerichtet zu kleineren Werten der Straf-Funktion, bis ein Minimum erreicht wird (möglichst Strafe=0).
- Wurde eine gültige Lösung gefunden (Strafe=0), so bewegt sich ein lokales Suchverfahren zielgerichtet zu kleineren Werten der Gütekriterien, bis ein Minimum erreicht ist.
- Die erreichten Minima können bei ungünstigen Zielfunktionen auch lokale Minima sein (Senken in der Oberfläche).
- Man weiß bei komplexen Problemen meist nicht, ob man wirklich das globale Optimum erreicht hat.
Die Zielfunktion in unserem Beispiel ist "gutmütig". Die Bewertungsgrößen werden repräsentiert durch stetig gekrümmte, nicht wellige Funktionen.
Experiment duplizieren
OptiY bietet die Möglichkeit, für ein Projekt mehrere Experimente zu verwalten. So können wir die bisherigen Einstellungen beibehalten und als Ausgangspunkt für ein neues Experiment nutzen:
- Nach dem Duplizieren des Experiments erscheint im OptiY-Explorer die Kopie als Experiment2.
- Dieses weitere Experiment besitzt am Anfang die gleiche Konfiguration wie das Original. Nur die Anzeigefenster muss man neu definieren.
- Verwaltet man mehrere Experimente in einem Projekt, so sollte man mittels Umbenennen dafür sinnvolle Namen vergeben:
- Das bisherige Experiment könnte man z.B. Globale Suche nennen.
- Für das neue Experiment bietet sich die Bezeichnung Lokale Suche an:
Lokale Suche konfigurieren
Für jedes Experiment wird von OptiY ein separater Workflow verwaltet, so dass darin unabhängig voneinander Änderungen vorgenommen werden können:
- Zuerst selektieren wir die Lokale Suche über das Kontextmenü als Startup-Experiment, damit wir es bearbeiten können.
- Wir aktivieren den Nennwert der Dicke als Variable in den Grenzen von 0,3 mm ... 0,8 mm.
- Für die Optimierung wählen wir das Hooke-Jeeves-Verfahren mit Startschrittweite=Standard.
- Wir erhöhen die Zahl der Optimierungsschritte=1000 (mittels manuellem Stop
 können wir jederzeit die Berechnung anhalten).
können wir jederzeit die Berechnung anhalten). - Für alle Nennwerte und Bewertungsgrößen öffnen wir ein Nennwert-Diagramm, indem wir mit dem Cursor jede Größe einzeln in den Grafikbereich ziehen.
Wichtig:
Bevor wir die Berechnung starten, überprüfen wir jedesmal im Windows-Taskmanager, ob der Prozess Inventor.exe bereits aktiv ist. Wenn ja, so beenden wir diesen Prozess, weil ansonsten zusätzlich eine weiterer gestartet wird und der Hauptspeicher irgendwann überläuft!
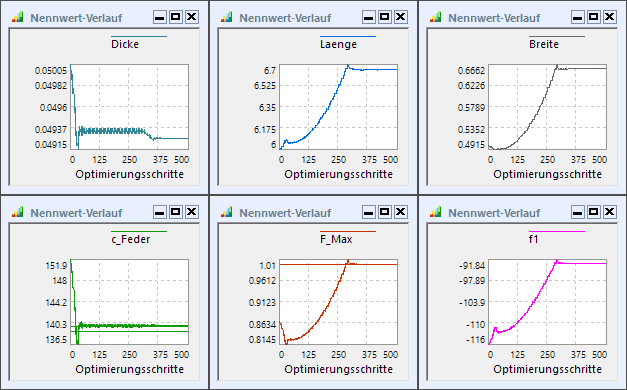
Nach dem Start der Optimierung ergibt sich folgende zielgerichtete Veränderung der Abmessungen:
- Um eine möglichst große Resonanzfrequenz zu erreichen, werden alle Abmessungen zielstrebig verkleinert!
- Das Optimum liegt in der Nähe von Null und wird dann nur durch die maximal mögliche Belastung begrenzt.
- Da haben wir eine wichtige Anforderung vergessen: Eine maximal sinnvolle Durchbiegung s, welche z.B. 10% bezogen auf die Feder-Länge nicht überschreitet!
Problem-Reduktion durch Erkenntnis
Man könnte nun eine zusätzliche Restriktionsgröße "Biegung" im Workflow ergänzen, deren oberer Grenzwert die maximal zulässige prozentuale Durchbiegung beschreibt:
- Darauf verzichten wir jedoch, weil im Ergebnis die Länge der Biegefeder sich exakt auf das maximal zulässige Verhältnis einstellen würde. Dies ist dadurch bedingt, dass die Biegefeder wegen der geforderten hohen Resonanzfrequenz möglichst sein klein wird.
- Wir können deshalb mit dieser Erkenntnis das Optimierungsproblem vereinfachen, indem wir die Laenge als Konstante einstellen und den Wert vorgeben:
- Laenge = 10 * s = 10 * F/c_Feder = 10 * 1 N/140 N/m = 0,0714 m
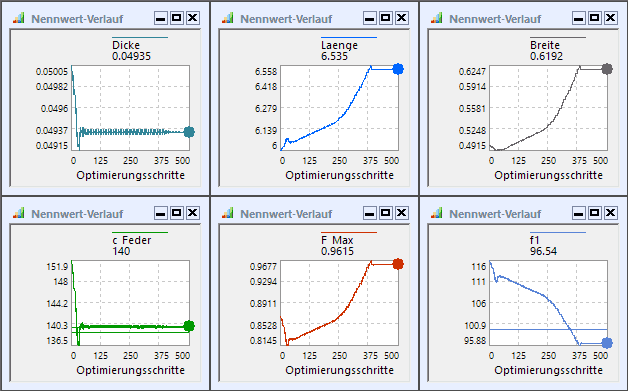
- Nun wird die geforderte Federkonstante sehr schnell erreicht, wobei sich die Resonanzfrequenz f1 im Beispiel zufällig bereits vergrößert:
- Nach Erreichen der zulässigen Federkonstante sollte das Optimierungsverfahren sich nun eigentlich der weiteren Erhöhung der Resonanzfrequenz widmen, da diese als Gütekriterium definiert ist.
- Leider scheint dies mit der aktuellen Konfiguration unseres Optimierungsexperiments nicht zu gelingen.
Problem der Randoptima
Bei technischen Problemstellungen wird die optimale Lösung meist an Restriktionsgrenzen liegen, weil die zu berücksichtigenden Anforderungen oft entgegensetzt wirken. Das führt an Restriktionsgrenzen mit großer Wahrscheinlichkeit zu Problemen der Konvergenz in Richtung einer optimalen Lösung:
- Bei der in OptiY verwendeten hierarchischen Optimierungsstrategie wird aus den aktuellen Restriktionsverletzungen der Wert einer Straf-Funktion berechnet.
- Um zuerst alle Forderungen zu erfüllen, hat die Minimierung des Straf-Funktionswertes die höchste Priorität.
- Erst wenn alle Forderungen erfüllt sind (Straf-Funktionswert=0), widmet sich die Optimierungsstrategie der Verfolgung unserer Wünsche (Minimierung der Gütekriterien).
- Eine bessere Erfüllung unserer Wünsche (Resonanzfrequenz vergrößern) führt zwangsläufig wieder zu Restriktionsverletzungen (zu große Federkonstante).
- Damit schaltet der Optimierungsprozess an dieser Stelle ständig zwischen zwei Zielfunktionen hin und her (Forderungen und Wünsche).
- Die Konvergenz zur optimalen Lösung wird damit meist "zuverlässig" verhindert!
Dieses Problem lässt sich zum Glück einfach lösen, indem man alle Wünsche als Forderungen formuliert:
- Diese Änderung führen wir über den Workflow-Editor durch.
- Wir löschen das Gütekriterium "f1" und ergänzen eine neue Restriktionsgröße, die wir ebenfalls "f1" nennen.
- Wir verknüpfen diese Restriktionsgröße mit der zugehörigen Ausgangsgröße "_f1" des Modells, das negative Vorzeichen ist nun nicht mehr erforderlich!
- Als unteren Grenzwert geben wir auf Grund unserer Vorkenntnisse eine anzustrebende Resonanzfrequenz ein (z.B. 300 Hz).
- Der obere Grenzwert sollte ungefähr um den gleichen Wert darüber liegen (z.B. 600 Hz), weil die Breite des zulässigen Wertebereiches einen Einfluss auf den Strafwert bei Restriktionsverletzung hat.
- Unser Gütekriterium "Resonanzfrequenz" ist nun selbst Bestandteil der Straf-Funktion und es existieren keine separaten Gütekriterien.
- Damit entfällt das Umschalten zwischen den Zielfunktionen an den Restriktionsgrenzen und das Verfahren sollte numerisch stabil auf der Straf-Funktion zum Optimum konvergieren:
- Leider wird das Ergebnis ähnlich schlecht aussehen, solange der zulässige Bereich für c_Feder=139...140 N/m sehr eng gewählt ist.
- Ein relativ zum Absolutwert sehr schmaler zulässiger Bereich wird als sehr wichtig angesehen. Kleine Abweichungen werden damit überbewertet und die Optimierung kann sich in diesem schmalen Bereich verfangen.
- Die Federkonstante tendiert aufgrund der Maximierung der Resonanzfrequenz zu höheren Werten.
- Wir können deshalb die untere Grenze c_Feder=0 N/m setzen.
- Dadurch wird die Strafzielfunktion insgesamt "sanfter" und die Optimierung sollte voranschreiten:
- Die Erhöhung der Resonanzfrequenz erfolgt durch Vergrößern der Dicke und Verringern der Breite.
- Bei letzterem stört der untere Grenzwert für die Breite.
- Wir erweitern die Grenzen für beide Maße auf 0,3...8 mm und starten die Optimierung erneut:
Abhaengigkeiten zwischen Optimierungsvariablen
Das Ergebnis tendiert zu Dicke >> Breite ("Hochkant-Feder") und wird dadurch praktisch unbrauchbar:
- Die Feder könnte nun zur Seite wegknicken.
- Die Frequenz der seitlichen Grundschwingung wird minimiert, was kontraproduktiv zur Maximierung der Resonanzfrequenz ist.
Die im Sinne maximaler Resonanzfrequenz optimierte Feder muss also einen quadratischen Querschnitt besitzen (Dicke=Breite):
- Auch hier verzichten wir auf das Hinzufügen einer weiteren Restriktion, welche "Hochkant-Federn" verhindert.
- Wir vereinfachen stattdessen das Optimierungsproblem auf eine Optimierungsvariable (Breite als Kantenlänge des Quadrats):
- Löschen von Entwurfsgröße-Nennwert Dicke im Workflow.
- Einfügen einer Transfervariablen mit gleichem Name Dicke, welche ihren Wert vom Nennwert Breite erhält.
- Benutzung der Transfervariablen als Eingang für das CAD-Modell und Verknüpfung mit dem Dicken-Parameter t_xx des CAD-Modells:
Nach Start der Optimierung sollte sich nun ein quadratischer Querschnitt ergeben, welcher exakt die geforderte Federkonstante realisiert:
- Wichtig: Die im obigen Bild sichtbare nur geringfügig erhöhte Wert für die Federkonstante ergibt sich erst, wenn man den Gewichtsfaktor für die Restriktionsgröße c_Feder entsprechend erhöht.
- Da die mit der anderen Restriktion f1 geforderte Resonanzfrequenz nicht erreicht werden kann, strebt das Optimierungsverfahren eine Kompromisslösung an, bei welcher die Summe der Strafpunkte minimal wird. Den Anteil der einzelnen Restriktionen an den Strafpunkten kann man über die Gewichtsfaktoren steuern.
CAD-Modell mit Bestwert konfigurieren
Die mittels der lokalen Suche gefundene optimale Lösung kann man sich als Bestwert-Parameter anzeigen lassen:
- Das CAD-Modell enthält noch immer die Parameter-Konfiguration der Ausgangslösung, weil wir sinnvoller Weise auf ein Speichern des Bauteils bei jedem Optimierungsschritt verzichtet haben.
- Diese Ausgangslösung sollte man für die lokale Suche im OptiY-Experiment nicht durch den Bestwert überschreiben, um die Nachvollziehbarkeit des Optimierungsprozesses zu gewährleisten. Deshalb darf man NICHT für den "Bestwert > Parameter übernehmen"!
Die Überführung der Parameter der optimalen Lösung in das CAD-Modell erfolgt in folgenden Schritten:
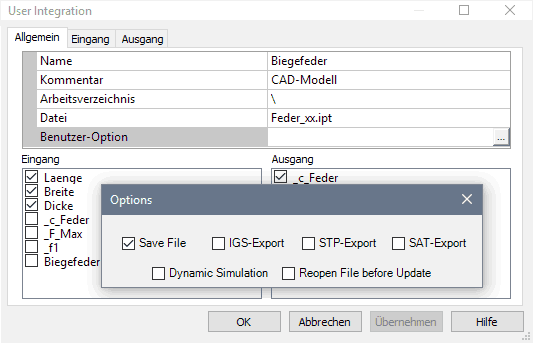
- Benutzer-Option > File Export=Save aktivieren für das Inventor-Modell im Workflow:
- Analyse > Bestwert > Simulation durchführen speist die optimalen Parameter (Bestwert) ins CAD-Modell, welches nach der Simulation mit diesen Werten gespeichert wird.
- Benutzer-Option > File Export wieder deaktivieren!
- Autodesk Inventor starten im Windows und die optimale Konfiguration des Bauteils überprüfen.