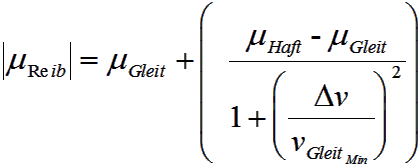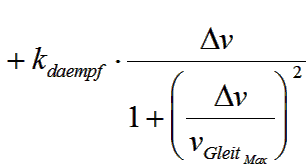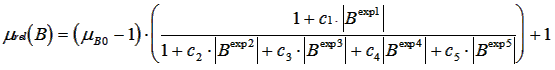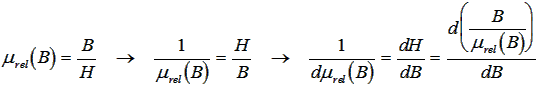Software: SimX - Parameterfindung - Permeabilitaet - Effekt-Modellierung
Leider sind viele Effekte, welche in Modellen feinwerktechnischer Antriebe nicht vernachlässigt werden können, nur unzureichend erforscht. Dies betrifft z.B. die Phänomene der mechanischen Reibung oder die Magnetisierung von Eisenwerkstoffen in Magnetkreisen. Je nach Kenntnisstand zu dem betreffenden Effekt bildet man die Abhängigkeiten über geeignete mathematische Funktionen ab.
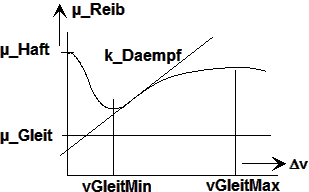
Beispiel: Reibung
Man beachte, dass für den Reibeffekt im Beispiel ein Funktionsansatz so gewählt wurde, dass die benötigten Parameter physikalisch-technischen Kennwerten ausgewählter Zustände entsprechen (Geschwindigkeiten, Reibwerte). Für die Nutzung von Modellansätzen im Ingenieurbereich sollte dies immer angestrebt werden!
Beispiel: Magnetisierung
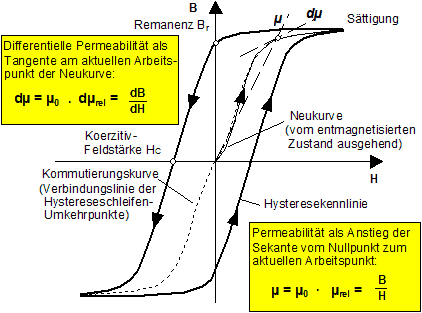
Beim Auf- bzw. Abmagnetisieren von Eisen entstehen Schleifen der Magnetisierungskurve, deren Breite von der Aussteuerung in den Umkehrpunkten abhängt:
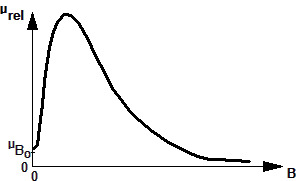
Die Nachbildung dieser Magnetisierungshysterese ist sehr aufwändig und noch nicht allgemeingültig gelöst. Für viele Anwendungsfälle genügt die Nachbildung der Neukurve, welche praktisch mit dem Verlauf der Kommutierungskurve übereinstimmt. Es besteht dann ein eindeutiger Zusammenhang zwischen der Flussdichte B und der Feldstärke H, der über eine Funktion µrel=f(B) dargestellt werden kann:
Der Verlauf dieser Funktion kann z.B. durch einen gemischten Polynom-Ansatz nachgebildet werden:
- Bei der Flussdichte Null besitzt das Eisen eine Anfangspermeabilität µB0.
- Der Anstieg der Permeabilität von der Anfangspermeabilität ausgehend wird vor allem durch die Parameter c1 und exp1 bestimmt.
- Das Polynom im Nenner sorgt für die Verformung des Funktionsverlaufes in Richtung Sättigung (µrel=1 für B=∞).
- Die Exponenten sind reelle Zahlen.
Die Permeabilität wird durch die Sekante B/H zum Nullpunkt beschrieben:
- Je nach Art des Modellansatzes benötigt man unter Umständen auch die differentielle Permeabilität, welche als Tangente dB/dH definiert ist (Anstieg am aktuellen Arbeitspunkt).
- Aus obiger Funktion µrel(B) kann über folgende Schritte eine Funktion dµrel(B)=dB/dH gebildet werden:
- Nach Einsetzen der Funktion µrel(B) erhält man einen Ausdruck, der durch Anwendung der Quotientenregel nach der Flussdichte B ableitbar ist.
- Die Invertierung dieser Ableitung ergibt dann die gewünschte Funktion dµrel(B), welche die gleichen Parameterwerte für c1 bis c5 und exp1 bis exp5 besitzt wie die Funktion µrel(B).
- Der Funktionswert für B=0 ist bei beiden Funktionen gleich der relativen Anfangspermeabilität µB0.
- Die Parameter für diesen Modellansatz sind weitestgehend abstrakte Koeffizienten, nur die Anfangspermeabilität besitzt eine physikalisch-technische Entsprechung.
Fazit
Es lassen sich beliebig viele mathematische Funktionen definieren, welche einen bestimmten Zusammenhang (Effekt) zwischen mehreren physikalisch-technischen Größen nachbilden. Die Parameter dieser mathematischen Funktionen dienen primär nur der Erzielung des gewünschten Funktionsverlaufes und haben häufig keine physikalisch-technische Entsprechung. Es sollten bevorzugt Funktionen genutzt werden, deren Parameter physikalisch-technische Entsprechungen aufweisen.