Software: SimX - Nadelantrieb - Wirkprinzip - Zielfunktion

↑

← →

Experiment: Hierarchische Optimierung

Globale Suche

Die zuvor angewandte Rastersuche gehört zu den globalen Suchverfahren. Damit werden Informationen über den gesamten aufgespannten Suchraum gewonnen. Solche Informationen zu den Eigenschaften der Gütefunktion sind äußerst nützlich für den Optimierungsprozess:

• Existieren mehrere lokale Optima?
• Existieren voneinander getrennte Bereiche zulässiger Lösungen?
• Liegen Optima direkt an Grenzen zum Bereich unzulässiger Lösungen?
• Ist die Gütefunktion numerisch kritisch (unstetig, verrauscht, Polstellen usw.)?

Globale Suche setzt meist eine Reduktion des Suchraums voraus (Rechenzeit!):

• Ausnutzung von Abhängigkeiten zwischen den Entwurfsparametern.
• Berücksichtigung von bereits erarbeitetem Wissen zum Optimalwert einzelner Entwurfsparameter.
• Die erforderliche Reduktion auf 2 bzw. maximal 3 Entwurfsparameter gelingt nur in den ersten Etappen eines Optimierungsprozesses.
  

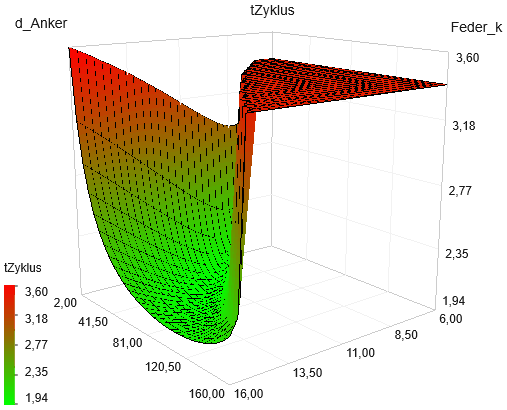
Die gesamte Gütefunktion wie im obigen Bild bekommt man bei praktischen Optimierungsproblemen eher selten zu Gesicht. Deshalb sollte man zumindest ein Gefühl dafür entwickeln, wie ausgehend von einem Startpunkt mit lokalen Suchverfahren eine optimale Lösung auf der "unsichtbaren" Gütefunktion gefunden wird:

• Wir hatten bereits festgestellt, dass innerhalb des Suchraums zwei unterschiedliche Bereiche existieren:
  • Bereiche mit zulässigen Lösungen (alle Forderungen werden erfüllt).
  • Bereiche unzulässiger Lösungen (es werden Restriktionen verletzt).
• Zusätzlich existiert noch der Bereich außerhalb des Suchraums:
  • Enthält alle Lösungen, von denen mindestens ein Entwurfsparameter außerhalb der festgelegten Grenzen liegt.
  • Mit Ausnahme der Rastersuche können bei anderen Optimierungsverfahren während des Suchprozesses auch Lösungen außerhalb des Suchraums generiert werden! Für diese Lösungen wird dann jedoch kein Simulationslauf durchgeführt.

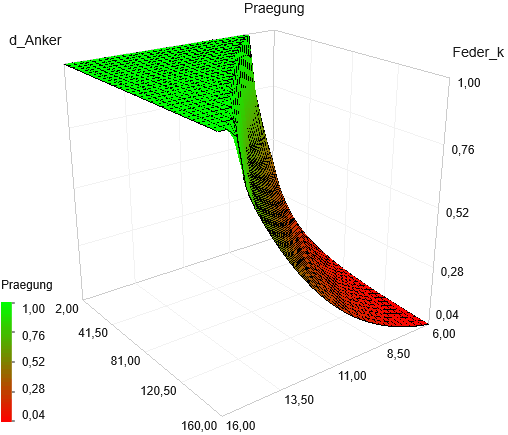
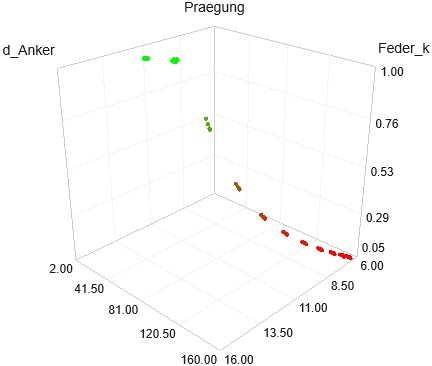
Die 3D-Darstellung der Restriktionsgröße Praegung zeigt die Abgrenzung zwischen zulässigen (=1) und unzulässigen Lösungen (<1) im Suchraum:

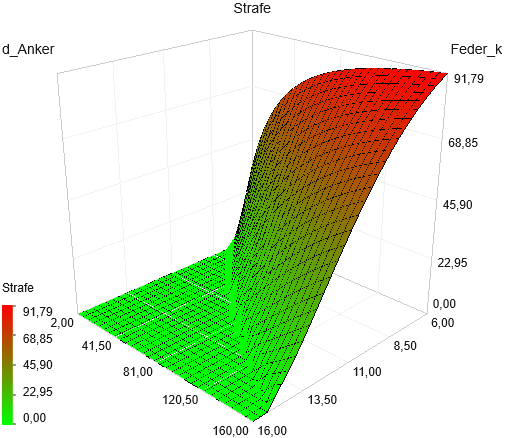
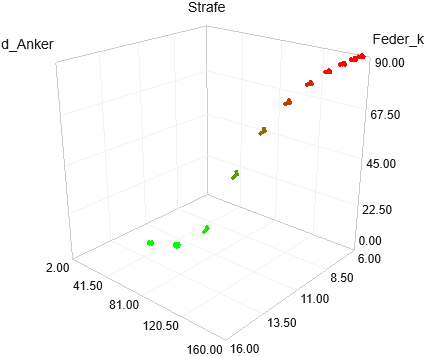
Zusätzlich wird automatisch eine Straffunktion als Bestandteil der Gütekriterien generiert, wenn Restriktionen definiert wurden. In der 3D-Darstellung der Straffunktion bilden sich die Lösungsbereiche wie folgt ab (Strafe=0 sind die zulässigen Lösungen):

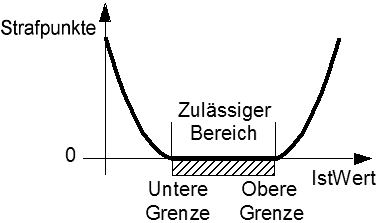
Restriktionsverletzungen werden dabei nach folgendem Prinzip mit "Strafpunkten" bestraft:

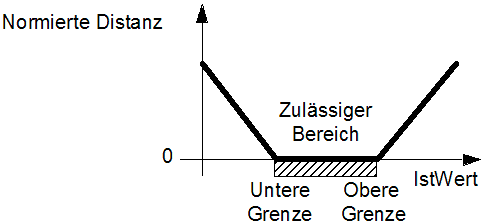
• Für jede Restriktionsgröße wird die Distanz zum zulässigen Wertebereich berechnet (UG=untere Grenze / OG=obere Grenze):

Distanz = 0	: wenn UG ≤ Istwert ≤ OG)
Distanz = abs (IstWert-OG)	: wenn IstWert > OG
Distanz = abs (IstWert-UG)	: wenn IstWert < UG

• Es erfolgt eine Normierung der Distanz auf die Bereichsbreite:

NormDistanz = Distanz/Bereich mit Bereich = abs (OG-UG)

• Die normierte Distanz repräsentiert die Stärke der zugehörigen Restriktionsverletzung und kann als Maß für die "Bestrafung" des Modellverhaltens dienen.
• Ein quadratischer Ansatz für die Berechnung der Strafpunkte aus der normierten Distanz wichtet den Grad der jeweiligen Restriktionsverletzung:

Strafpunkte = Wichtung · NormDistanz²

• Der Wert der "Strafe"-Funktion ergibt sich als Summe der Strafpunkte aller Restriktionen.

Hierarchische Zielfunktion

OptiY nutzt die vom Nutzer formulierten Gütekriterien als Bestandteil einer "hierarchischen" Zielfunktion:

• Um zwei Lösungen miteinander vergleichen zu können, muss für jede dieser Lösungen ein Zielfunktionswert nach der gleichen Zielfunktion gebildet werden. Der Zielfunktionswert entspricht der "Güte" oder "Fitness" einer Lösung.
• OptiY verwendet dafür drei verschiedene Zielfunktionen

1. Straf-Funktion für die Begrenzung des Suchraums (Tool-interne "unsichtbare" Größe)
2. Straf-Funktion für Restriktionsverletzungen (zusätzliches Gütekriterium "Strafe")
3. Gütekriterien für zulässige Lösungen (vom Nutzer definiert)

• Die 1. Zielfunktion hat eine höhere Priorität als die 2. Zielfunktion. Diese hat eine höhere Priorität als die 3. Zielfunktion.
• Für den Vergleich zweier Lösungen wird die zuständige Zielfunktion mit der höchsten Priorität benutzt, z.B.:

1. Liegt mindestens eine Lösung außerhalb des durch die Grenzen der Entwurfsparameter aufgespannten Suchraums, so wird die 1. Zielfunktion benutzt.
2. Gibt es bei mindestens einer Lösung noch Restriktionsverletzungen, so wird die 2.Zielfunktion benutzt ("Strafe").
3. Nur wenn beide Lösungen im zulässigen Bereich liegen, werden die nutzerdefinierten Gütekriterien für die Bewertung benutzt.

• Der Wert von "Strafe" ist Null, wenn keine Restriktionen verletzt sind (Bereich zulässiger Lösungen im zulässigen Suchraum).
• Im Bereich unzulässiger Lösungen steigt der Wert der Straffunktion quadratisch mit dem Grad der Restriktionsverletzung, wie es zuvor erläutert wurde.

Lokale Suche - Visualisierung von Suchpfaden

Aufbauend auf dem Experiment Rastersuche 2D definieren wir durch Duplizieren ein neues Experiment Suchpfade:

• Zur Optimierung wählen wir das Hooke-Jeeves-Verfahren mit:
  • Startschrittweite = Manuell
  • Auto-Stop = Automatischer Stop
• Ausgehend von unterschiedlichen Startpunkten wollen wir den Pfad des Verfahrens im Suchraum beobachten.

Hooke-Jeeves-Verfahren

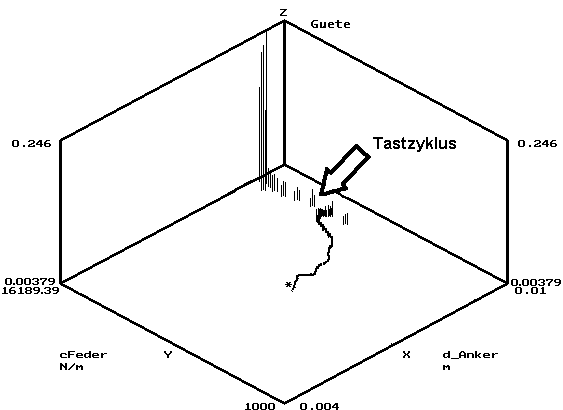
Die Wirkungsweise eines lokalen Suchverfahrens, welches die 1. Ableitung am aktuell erreichten Ort durch Abtastung der Zielfunktion ermittelt, soll am Beispiel des gewählten Hooke-Jeeves-Verfahrens erläutert werden:

• Die Steigung der Zielfunktion am Punkt der aktuell erreichten Lösung wird über kleine Tastschritte ermittelt. Die genutzte Tastschrittweite muss dabei der Oberfläche der Zielfunktion angepasst sein.
• In Richtung des ermittelten steilsten Abstiegs wird anschließend ein größerer Schritt ausgeführt:
  
• Die Tastschritte werden gleichzeitig zur Verbesserung der Lösung genutzt. Beim Tastzyklus wird von einem Startvektor aus nacheinander in jede Koordinatenrichtung ein diskreter Suchzyklus durchgeführt. Führt dabei der Tastschritt in einer Richtung nicht zum Erfolg (Verbesserung des Gütewertes), so wird zusätzlich die entgegen gesetzte Richtung abgetastet.
• Nach einem Tastphase erfolgt die Extrapolation. In Richtung des ermittelten steilsten Abstieges wird ein größerer Schritt ausgeführt. Ein erneuter Extrapolationsschritt ist immer doppelt so groß wie der vorherige, solange dabei eine Verbesserung des Zielfunktionswertes erreicht wird. Schießt das Verfahren über den tiefsten Punkt hinaus oder in einen verbotenen Bereich, erfolgt eine schrittweise Verringerung der Extrapolationsschrittweite.
• Das Hooke-Jeeves-Verfahren regelt die anfängliche Tastschrittweite herunter, wenn längere Zeit keine Verbesserung des Zielfunktionswertes mehr erreicht werden konnte. Meist gelangt dann diese Schrittweite in Größenordnungen der stochastischen Rauigkeiten der Zielfunktion und das Optimierungsverfahren bleibt "hängen", weil die partiellen Ableitungen total verfälscht werden (die reale Steigung wird nicht mehr erkannt!).

Suchpfad ohne Restriktionsverletzungen

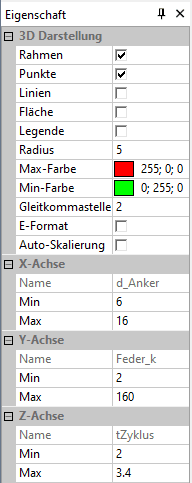
• Wir konfigurieren erneut eine 3D-Darstellung für tZyklus=f(d_Anker, Feder_k).
• Zuerst starten wir starten in der oberen Ecke der Gütefunktion mit Startwerten, welche ein sicheres Prägen ermöglichen:
  • d_Anker=15 mm mit Startschrittweite=0,2 mm
  • Feder_k=5 N/mm mit Startschrittweite=2 N/mm
• Die Anfangswerte für die Entwurfsparameter liegen nicht direkt an der Grenze des Suchraumes, um die lokale Abtastung der Steigung am Rand nicht zu behindern.
• Die Startschrittweiten sind in Bezug auf die Suchraumgrenzen relativ zueinander ungefähr gleich groß. Sie wurden so gewählt, dass man optisch die einzelnen Stützstellen der lokalen Abtastung im 3D-Diagramm unterscheiden kann.

• Während der Lösungssuche erfolgt standardmäßig eine automatische Skalierung der Koordinatenachsen unseres 3D-Diagramms (nur Punkte zur Darstellung wählen!):
  • Um eine bessere Vergleichbarkeit mit den 3D-Flächen der vorherigen Rastersuche zu erreichen, setzen wir nach dem Erreichen des Optimums für das Diagramm Auto-Skalierung=False.
  • Für die X- und Y-Achse tragen wir die Grenzen des kompletten Suchbereichs ein.
  • Die Grenzen der Z-Achse passen wir entsprechend der individuell ermittelten Funktionswerte an:
    
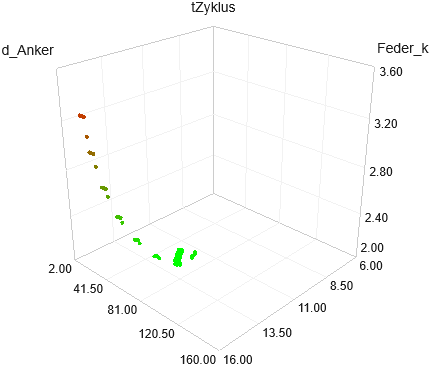
• Während der Suche wird der Bereich zulässiger Lösungen im Beispiel nicht verlassen:
  • Das Optimierungsverfahren bewegt sich deshalb näherungsweise entlang des steilsten Abstiegs der Gütefunktion tZyklus=f(d_Anker, Feder_k) zum flachen und lang gestreckten Talgrund.
  • In der Talmulde erfolgt eine Neuorientierung für die Suchrichtung mit einer Drehung von ca. 90° und das Verfahren wandert in der Mulde bis zum tiefsten Punkt (Bestwert).

Suchpfad beginnend mit Restriktionsverletzungen

Mit den Startwerten (ohne Änderung der Startschrittweiten)

• d_Anker=6,2 mm und
• Feder_k=155 N/mm

konfigurieren wir einen Antrieb, der sich fast nicht mehr bewegt (Praegung ca. 0.05).

Anhand des Pfades auf der Funktion tZyklus=f(d_Anker, Feder_k) kann man noch nicht direkt erkennen, wie das Optimierungsverfahren den zulässigen Bereich der Lösungen findet:

• Das Optimierungsverfahren erreicht den zulässigen Bereich der Lösungen in der flachen Mulde der Gütefunktion.
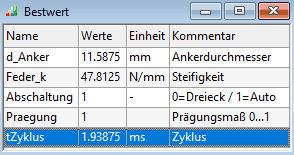
• In der Mulde wird letztendlich wieder die gleiche Lösung mit minimaler Zykluszeit gefunden. Die Abweichung zwischen den ermittelten Bestwerten bewegt sich im Bereich des numerischen Rauschens.

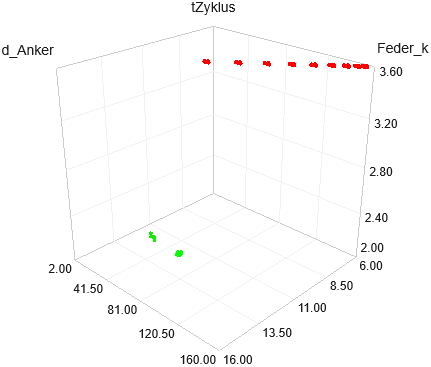
Das Prinzip der hierarchischen Optimierung wird deutlicher, wenn man sich die 3D-Darstellung von Strafe=f(d_Anker, Feder_k) anschaut:

• Infolge der Restriktionsverletzung Praegung<1 ist der Wert der Straffunktion zu Beginn der Optimierung nicht Null.
• Deshalb erfolgt die Optimierung in der ersten Phase nur auf der Straffunktion als Zielfunktion. Es wird näherungsweise der steilste Abstieg zum Gebiet mit Strafe=0 gesucht. Dabei steigt das erreichte Prägungsmaß stetig an:
  
• Erst wenn die Lösungssuche im zulässigen Bereich angekommen ist, erfolgt die Umschaltung der Zielfunktion auf das Gütekriterium tZyklus.
• Unabhängig vom Startpunkt sollte die lokale Suche des Hooke-Jeeves-Verfahrens im Beispiel immer das globale Optimum als Bestwert finden:

Beachte: Für die Einsendung der Lösung zur 1. Etappe ist diese Konfiguration des Suchpfad-Experimentes zu speichern!

← →