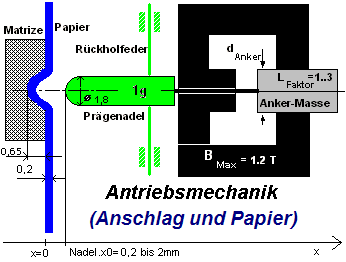
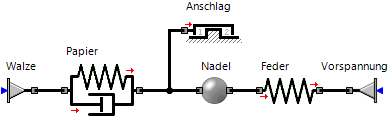
Software: SimX - Nadelantrieb - Wirkprinzip - Papier

↑

← →

Nadel-Anschlag

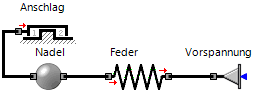
Die Bewegung der Nadel wird durch die Anschläge am Matrizenboden und in der Ruhelage begrenzt:

• Das Gestell der Antriebsbaugruppe bildet hierbei die neutrale Bezugsposition für beide Anschlag-Seiten (x=0 mm).
• Vereinfacht kann man die Stoßvorgänge an beiden Seiten als ideal plastisch an starren Anschlägen betrachten (nach dem Stoß → Nadel.v=0 m/s).
• In der Modell-Bibliothek stehen für die "Translatorische Mechanik (1D)" zwei Elementtypen für "Anschläge" zur Verfügung:
  1. Der allgemeine "Anschlag", welcher auch eine veränderliche neutrale Position ermöglicht (relativer Anschlag zwischen zwei beweglichen Elementen),
  2. Der vereinfachte "Anschlag gg.Absolut", welche nur für eine fixe neutrale Position genutzt werden kann (absoluter Anschlag eines beweglichen Elementes an ein feststehendes Element).
• Wir wählen das vereinfachte Anschlagselement, da es numerisch robuster und schneller arbeitet als der relative Anschlag.
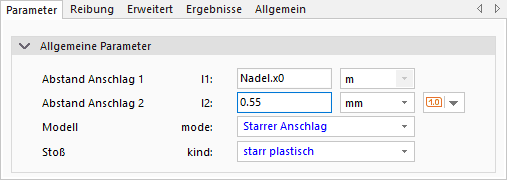
• Wir konfigurieren das Anschlagselement als "Starren Anschlag" mit "Plastischem Stoß" ohne "Reibung":
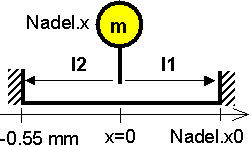
  • Nach dem Prägen des Papiers befindet sich zwischen Nadelspitze und Matrizenboden eine Papierschicht von ca. 0,1 mm Dicke. Dies entspricht einem Anschlag bei -0,55 mm auf dieser Seite.
  • Die Parameter l1 und l2 beschreiben die Abstände der beiden Anschlagspositionen in Bezug auf die neutrale Position x=0 mm (in der "Mitte"):
    
  • Die Parameterwerte l1 und l2 für die Abstände vom neutralen Punkt (x=0 mm) sind beide positiv:
    
  • Hinweis: Die Zuordnung von l1 und l2 anhand der Elementdokumentation ist nicht intuitiv, sondern wurde durch Trial & Error verifiziert!
  • Innerhalb des Wegabschnittes (l1+l2) ist die Kraftwirkung auf ein sich darin bewegendes Element (hier die Nadel-Masse) gleich Null.
  • An den Begrenzungen dieses Wegabschnittes (den Anschlägen) wird eine Kraft erzeugt, welche das bewegte Element kurzfristig auf v=0 m/s abbremst und die weitere Bewegung über die Anschlagsposition hinweg verhindert (plastischer Stoß).
• Achtung: Nach Hinzufügen solch eines "komplexen" Modell-Elements sollte man sofort überprüfen, ob es sich wie gewünscht verhält!
  • Die Begrenzung der Nadelbewegung in beiden Richtungen kann man in einem gemeinsamen Experiment testen, indem man die Nadel mit ausreichender Geschwindigkeit in Richtung Matrize "schleudert".
  • Dazu setzt man Nadel.v0 auf einen hinreichend großen negativen Wert (im Beispiel: -4 m/s).
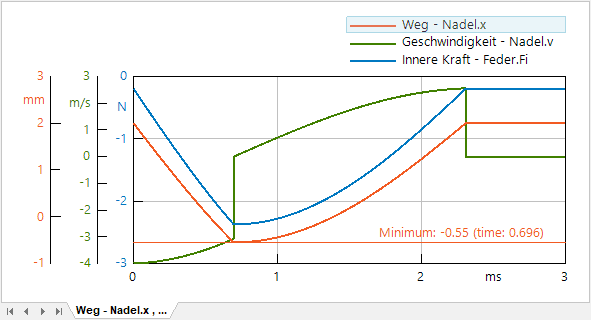
  • Bei -0.55 mm muss die Nadel sicher abgebremst werden. Die Feder holt dann die Nadel zurück.
  • Bei Nadel.x0 (im Beispiel: 2 mm) muss die Nadel wieder zur Ruhe kommen infolge der vorgespannten Feder (im Beispiel: um 1 mm in Bezug auf Nadel.x0):

• Hinweise:
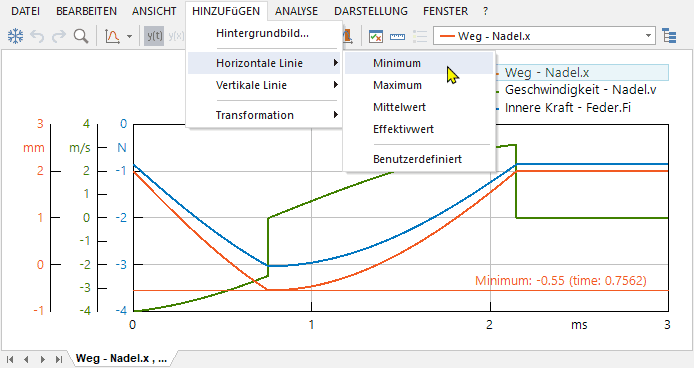
  • Die obige Konfiguration des Ergebnisfensters ist mittels der Eigenschaftsleiste vorzunehmen. Die erforderlichen Grundlagen dafür haben wir uns während Vorbereitung zu dieser Übungsetappe erarbeitet.
  • Die Signale wurden mit der Linienstärke=2 dargestellt, damit sie sich besser von den Linien des Fensters und des Signal-Panels abheben.
  • Um die maximale Vorschubbewegung für Nadel.x einfach überprüfen zu können, wurde zusätzlich eine horizontale Linie (Minimum) eingeblendet, welche für das aktuell ausgewählte Signal wirkt.
  • Die Zeit (time) für das Erreichen des Minimum ist abhängig von der konkreten Federsteife (Feder.k resultierte im Beispiel noch aus einem tZyklus=3,4 ms).

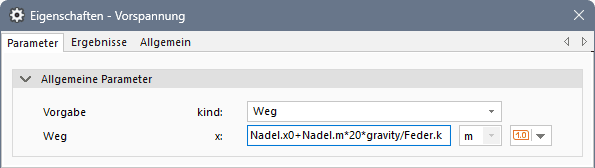
Vorspannung der Feder in der Ruhelage der Nadel

Bisher wurde zum Testen des Bewegungsablaufes der Prägenadel die Rückholfeder um einen konstanten Wert von 1 mm in der Ruhelage der Nadel vorgespannt. Soll unabhängig von der bewegten Masse und der Steife der Rückholfeder eine Stoßfestigkeit von 20g (20-fache Erdbeschleunigung) für das Verbleiben der Nadel in der Ruheposition erreicht werden, ist eine Anpassung an die aktuelle Konfiguration des Feder-Masse-Systems erforderlich:

• In Ruhe muss die Haltekraft der vorgespannten Feder dem 20-fachen Gewicht der bewegten Masse entsprechen, wenn ein Betrieb in horizontaler Lage angestrebt wird.
• Aus 20*g*Nadel.m = dx*Feder.k (mit dx=Vorspannung.x-Nadel.x0 und 1g=gravity) → Vorspannung.x = Nadel.m*20*gravity/Feder.k:
  
• Vor der Simulation mit der aktuellen Vorspannung muss man für die Feder die Protokollierung der Wegdifferenz Feder.dx aktivieren. Man kann dann nach der Simulation für die wieder eingenommene Ruhelage der Nadel den berechneten Vorspannweg der Feder als Wert von Feder.dx ablesen (im Beispiel ca. 0.2 mm).
• Der Einfluss dieser Vorspannungsänderung auf den Bewegungsablauf ist gering:
  

Papier

Das zu prägende Papier als Wirkstelle muss im Modell berücksichtigt werden, um Aussagen zur Eignung eines Wirkprinzips für den Aktor machen zu können. Im Beispiel wurden aus Messungen beim Prägevorgang folgende vereinfachte Zusammenhänge abgeleitet:

• Die Kraftwirkung des Papiers auf die Nadel ist Null, solange die Nadel die Papieroberfläche noch nicht berührt (Nadel.x>=0.2 mm).
• Während des Eindringens verhält sich die Papieroberfläche wie ein Feder-Dämpfer-Element:
  • k = 36500 N/m
  • b = 5.5 Ns/m
• Nach Erreichen der Rissposition xRiss = ‑0.39 mm entfällt der elastische Anteil der Kraft (Prägung durch Zerfasern des Papiers). Beim weiteren Eindringen wirkt nur noch der Dämpfungsanteil mit b=5.5 Ns/m.
• Bei der Rückbewegung der Nadel existiert kein Dämpfungsanteil der Kraft.
• Wir benutzen dafür ein Feder-Dämpfer-Spiel-Element aus der Bibliothek.

Diese ziemlich komplizierte Abhängigkeit der Kraft von der Nadelposition, der Bewegungsrichtung der Nadel und vom Zustand des Papiers wollen wir schrittweise nachbilden:

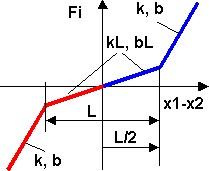
• Der Elementtyp "Feder-Dämpfer-Spiel" gestattet ähnlich wie der "Anschlag" die Modellierung eines Kraftelements mit einem Spielanteil (kräftefreie Nadelbewegung bis zur Papieroberfläche).
• Wir verwenden die Kraft-Kennlinie dieses Elementtyps als "Papier" und nutzen davon aber nur den blauen Bereich rechts von der Kennlinien-Mitte:
  
• Damit die Anfangsposition Nadel.x0 sich auf der Kennlinie bei (x1-x2)=0 befindet, muss man die Walzen-Seite vom "Papier" ebenfalls mit der Position Nadel.x0 belegen. Für die "Walze" auf der Seite von x1 des Papiers verwenden wir wieder ein Vorgabe-Element aus der Mechanik-Bibliothek mit der Funktion "Weg"-Vorgabe x: Nadel.x0:
  
• Wir konfigurieren das Papier zuerst ohne Berücksichtigung der Bewegungsrichtung der Nadel und des Papierzustands:
  • k = 36500 N/m (Steifigkeit bei Anlage);
  • b = 5.5 Ns/m (Dämpfung bei Anlage);
  • kL = 0 N/m (Steifigkeit im Spiel);
  • bL = 0 Ns/m (Dämpfung im Spiel);
  • L = 2*(Nadel.x0-0.0002) (Spiel); ← mit Papierdicke=0.2 mm
  • Anfangswerte für Feder und Dämpfer ohne Vorspannung;
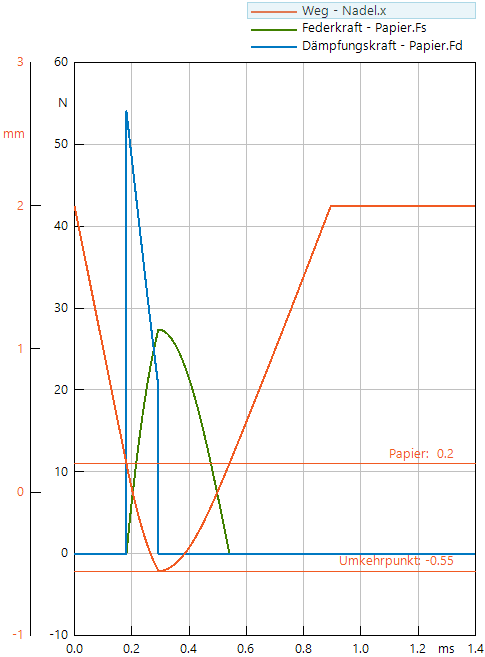
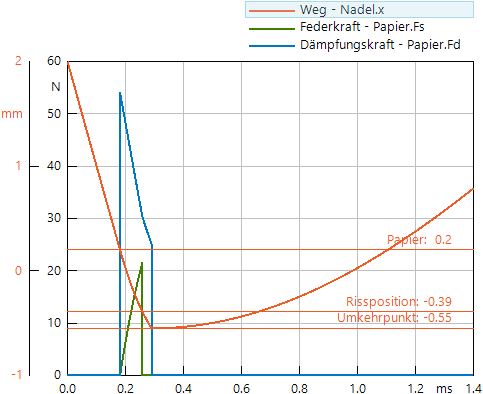
• Mit der Simulation sollte man dann sofort den richtigen Verlauf der vom Papier auf die Nadel ausgeübten Kraft überprüfen. Dazu "schleudert" man die Nadel wieder hinreichend kräftig in Richtung Papier (im Beispiel Nadel.v0=-10 m/s).
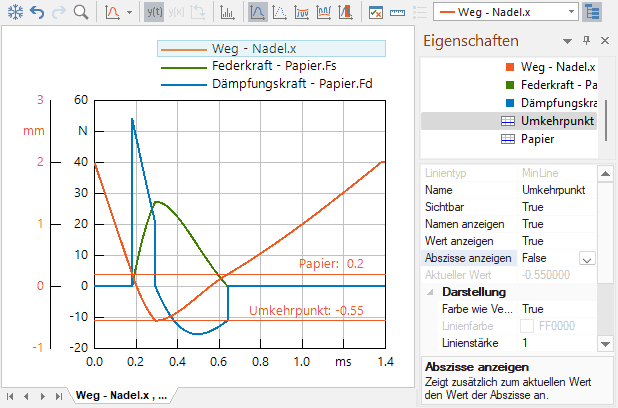
• Wir kontrollieren die relevanten Signalverläufe in einem neuen Ergebnisfenster, welches wir günstig konfigurieren:
  
  • Die Dämpfungskraft Fd=b*v ist eine Funktion der Eindring-Geschwindigkeit Nadel.v.
  • Die Federkraft Fs=k*x ist eine Funktion der Eindringtiefe Nadel.x.
  • Hinzufügen horizontaler Linien für markante x-Positionen erleichtert die Auswertung der berechneten Kraftverläufe:
    1. "Minimum" mit anschließendem Umbenennen des Namens und Ausblenden des Abszissenwertes zeigt die Position des Nadel-Umkehrpunktes (vollständiges Prägen bei -0,55 mm).
    2. "Benutzerdefiniert" mit dem Namen Papier und dem Wert 0.2 zeigt die Position der Papieroberfläche.
  • Befindet sich die Nadel oberhalb der Papieroberfläche, darf das Papier keine Kraft auf die Nadel ausüben!

• Wenn das Modellverhalten den Erwartungen entspricht, fügen wir nun die Richtungsabhängigkeit der Dämpfungskraft hinzu:
  b=5.5*0.5*(1-sign(Nadel.v))
  Die sign-Funktion kann nur die Werte (-1,0,+1) annehmen. Die Dämpfung soll Null sein, wenn sich die Nadel in Richtung der Ruhelage bewegt:
  
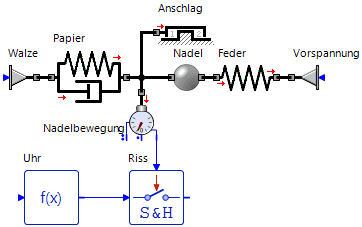
• Schwieriger ist die Berücksichtigung des Papierzustandes (glatt bzw. geprägt). Um diesen zu erfassen, muss man einen sogenannten "Ereignisbeobachter" installieren. Dieser überwacht mit Hilfe eines mechanischen "Bewegungsensors" die "Nadelbewegung". Erreicht die Nadel die Rissposition von ‑0.39 mm, so wird dies als Ereignis "Riss" registriert. Es hat sich als günstig erwiesen, dabei gleich den Ereignis-Zeitpunkt zu erfassen:
  
• Die "Riss"-Registrierung realisiert das spezielle Signalglied "Ereignisgesteuertes Abtastglied".
• Als "Uhr" kann das Signalglied f(x) verwendet werden (Funktionswert gleich aktuelle Simulationszeit time).
• Die Ereigniserkennung ist numerisch recht anspruchsvoll. Es darf nur das 1. Ereignis "Nadel erreicht Rissposition" registriert werden (danach ist das Papier "zerrissen").
• Als Ereignis soll nur die Bewegungsrichtung "von oben nach unten" registriert werden (von größeren x-Werten kommend).
• Der Grenzwert a=‑0.00039 [m] definiert die Position der Nadelspitze, wo das Ereignis stattfindet.
• Der Anfangswert für die Ausgangsbelegung ist y0=0.
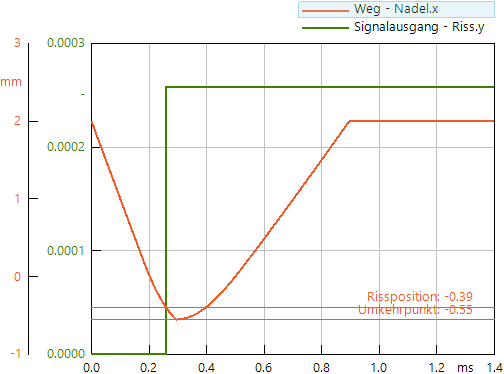
• Wir überprüfen mit der Simulation in einem neuen Ergebnisfenster, ob das Ereignis ordnungsgemäß registriert wird (zusätzliche benutzerdefinierte horizontale Linie=-0.39):
  
• Danach beziehen wir den Zustand des Papiers in die Kraftwirkung des Papier-Elements mit ein:
  k=36500*(1-sign(Riss.y))
• Da die Zeit time nicht negativ wird, kann die sign-Funktion hier nur die Werte 0 oder 1 annehmen!
• Wir überprüfen dann den vollständigen Verlauf der Papierkraft auf seine Glaubwürdigkeit:
  
• Hinweis: Falls sich das Modell der Antriebsmechanik einschließlich der Wirkstelle glaubwürdig und hinreichend richtig verhält, haben wir die erste Hürde überwunden! Nun können wir uns der eigentlichen Fragestellung dieser Entwurfsetappe widmen: "Ist ein E-Magnet als elektro-mechanischer Wandler geeignet?"
  ← →