Software: SimX - Nadelantrieb - Wirkprinzip - Optimierungsverfahren
Bisher haben wir unser Entwurfsproblem vor allem inhaltlich in eine Optimierungsaufgabe transformiert. Es fehlt nun noch die Konfiguration der "Numerik", d.h.: "Mit welchem Optimierungsverfahren soll die optimale Lösung gefunden werden?"
Leider ist das "optimale" Optimierungsverfahren und seine "optimale" Konfiguration abhängig von der Optimierungsaufgabe! Ausgehend von einer Standard-Konfiguration ist es meist günstig, einen gewissen Aufwand in den Abgleich des numerischen Verfahrens zu investieren. Das werden wir nun am Beispiel des Nadelantriebs üben:
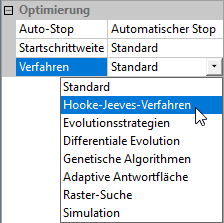
- OptiY bietet für den unerfahrenen Nutzer ein Standard-Verfahren an. Welches Verfahren sich dahinter verbirgt, ist abhängig von der Anzahl der Entwurfsparameter P und Gütekriterien K:
- Evolutionsstrategie bei K>1 oder P>9,
- Hook-Jeeves-Verfahren für K<2 und P<10
In unserem Beispiel würde also das Hook-Jeeves-Verfahren genutzt. Dieses tastet sich auf der Zielfunktion von der Ausgangslösung schrittweise in Richtung kleinerer Werte "bergab" und endet dort in der Talsohle - in der Hoffnung, dass dies das globale Optimum ist:
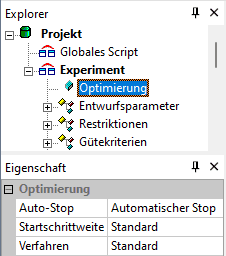
- Die Option "Automatischer Stop" soll die Suche beenden, wenn das Minimum erreicht wurde. Das dafür implementierte Kriterium funktioniert meist zuverlässig!
- Um an dieser Stelle zumindest einen Einblick in die Konfiguration eines Optimierungsverfahren zu erhalten, wählen wir das Hook-Jeeves-Verfahren:
- Die individuelle Abtast-Schrittweite für jeden Entwurfsparameter ist in der Standardeinstellung u.a. von deren vorgegebenem Variationsbereich [Untergrenze, Obergrenze] abhängig. Da dies numerisch nicht immer günstig sein muss, sollte man sich den Zugriff auf diese Abtast-Schrittweite ermöglichen, indem man Startschrittweite=manuell setzt.
- Die Startschrittweite erscheint dann als zusätzliche Eigenschaft nach Wahl des jeweiligen Entwurfsparameters im OptiY-Explorer.
- Die Abtastschrittweite für den aktuellen Wert des Entwurfsparameters darf innerhalb des vorgegebenen Suchbereiches [Untergrenze .. Obergrenze] nicht zu klein und nicht zu groß werden, damit die damit die Steigung an der Abtaststelle hinreichend genau berechnet werden kann.
- Aus Erfahrung sollte man bei der Bestimmung der Startschrittweite in folgender Reihenfolge vorgehen:
- Anfangswert der Entwurfsgröße → Startschrittweite ≈ Wert/50
- Überprüfen dieser Schrittweite für die Obergrenze → Startschrittweite ≥ Obergrenze/1000?
- Ist die Schrittweite für die Obergrenze zu klein, dann Startschrittweite ≈ Obergrenze/1000
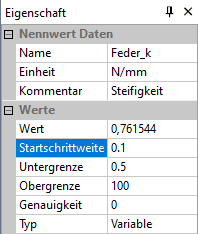
- Dies soll am Beispiel der Rückholfeder verdeutlicht werden, welche mit einem relativ kleinen Anfangswert im Verhältnis zur geschätzten Obergrenze beginnt:
- Hier ergibt sich bei der beschriebenen Vorgehensweise eine Startschrittweite von 0.1 N/mm ( 1/1000 von 100 N/mm). Auch wenn die Abtastschrittweite für den Anfangswert etwas zu groß ist, bei Bedarf verkleinert das Optimierungsverfahren die Abtastschrittweite bei mangelhafter Konvergenz!
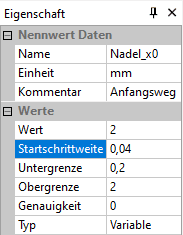
- Analog dazu sind die Abtastschrittweiten für die anderen Entwurfsgrößen zu wählen, wie dies beispielhaft für Nadel_x0 gezeigt ist.
- Hinweis: Ergeben sich laut Berechnung "krumme" Werte für die Startschrittweite, kann man auf nächstliegende anschauliche Werte runden (da es sich sowieso nur um grobe Schätzwerte handelt!).