Software: SimX - Nadelantrieb - Wirkprinzip - Lokale Suche
Experiment: Lokale Suche (Hooke-Jeeves)
Wichtig: Das SimulationX sollte jetzt mit dem soeben erfolgreich simulierten Modell geöffnet sein!
- Nach so viel Vorbereitung wollen wir nun im OptiY beherzt den Start-Button
 für das Experiment drücken und hoffen, dass sich der Antrieb in die gewünschte Richtung entwickelt:
für das Experiment drücken und hoffen, dass sich der Antrieb in die gewünschte Richtung entwickelt: - Wenn keine Verbesserung der Ergebnisse mehr zu erwarten ist, können wir das Experiment stoppen
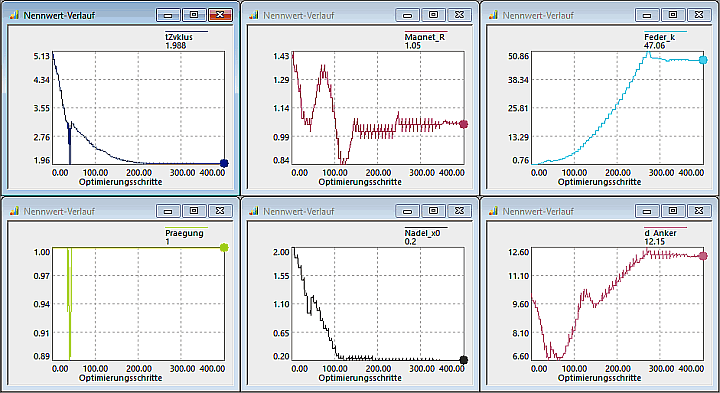
 (im Beispiel nach 400 Optimierungsschritten).
(im Beispiel nach 400 Optimierungsschritten). - Die Verkürzung der Zykluszeit wird vor allem erreicht durch eine Vergrößerung der Steifigkeit der Rückholfeder mit entsprechender Anpassung der anderen Antriebsparameter.
- Man kann sich die exakten Werte eines Optimierungsschrittes anzeigen lassen. Nach Doppelklick mit der linken Maustaste auf den gewünschten Kurven-Punkt wird dieser Punkt auf allen Kurven markiert und es werden die zugehörigen Werte eingeblendet. Ein Doppelklick abseits jeglicher Kurve blendet die Markierungen wieder aus.
Hinweise zur Fehlersuche:
Erkennt man ein fehlerhaftes Verhalten des Modells während der Optimierungsrechnung, so muss man das Experiment stoppen ![]() :
:
- Im SimulationX den Simulationslauf auf den Anfang zurücksetzen, damit ein definierter Beginn des nächsten Simulationslaufes stattfindet.
- Das Modellverhalten kann man dann im SimulationX mit den aktuell vom OptiY eingespeisten Nennwerten untersuchen.
Korrektur von Fehlern im SimulationX-Modell bei aktivem OptiY-Versuchsstand kann zum Absturz von OptiY führen, da die Verknüpfungen zwischen beiden Programmen dadurch fehlgeleitet werden:
- Vor der Fehler-Korrektur muss man OptiY beenden. Dabei bleibt das im SimulationX benutzte Modell offen. Da es mit den Parametern des letzten Simulationslaufes belegt ist, sollte man es schließen (ohne speichern!).
- Lädt man das Modell erneut im SimulationX, so besitzt es die Ausgangslösung als Parametersatz.
- Nach Korrektur der Modellfehler speichert man den neuen Modellzustand und schließt das Modell.
- In OptiY steht nach erneutem Start das korrigierte Modell im Experiment-Workflow zur Verfügung.
Typische Fehler-Situationen:
- Das Modell reagiert unglaubwürdig auf Nennwert-Änderungen:
- Hat z.B. die Änderung des Ankerdurchmessers keinen Einfluss auf die Bewegung, so fehlt die Verbindung zwischen dem OptiY-Workflow und dem Modellparameter oder etwas kann im Modell nicht stimmen!
- Erforderliche Modell-Änderungen muss man wie zuvor beschrieben vornehmen.
- Es wird keine Verbesserung der Anfangslösung erreicht:
- Das Modell rechnet zu ungenau, so dass durch die Abtastschritte kein Anstieg auf der Gütefunktion erkannt werden kann (Numerisches Rauschen):
- Wechseln in das SimulationX.
- Öffnen des Einstellungsdialogs für die Simulation.
- Verringern von absTol und relTol z.B. um 1 Zehnerpotenz auf 1E-6. (Achtung: höhere Genauigkeiten führen teilweise zu wesentlich längeren Rechenzeiten!).
- Verringern von dtMin auf z.B. 1E-12 (wesentlich kleinere Werte können zu numerischen Problemen führen!).
- In OptiY die Optimierung fortsetzen.
- Ungünstige Abtastschrittweiten für Entwurfsgrößen:
- Die Startschrittweite für die Abtastung wurde im Beispiel zu 1/50 des Startwertes (oder größer) gebildet.
- Reagiert das Modellverhalten sehr empfindlich auf eine Änderung des betreffenden Entwurfsparameters, so kann hier ein kleinerer Wert sinnvoll sein.
- Umgekehrt kann es auch sinnvoll sein, diese Startschrittweite zu vergrößern, falls die geringen Auswirkungen der Änderung ansonsten im numerischen Rauschen untergehen.
- Optimierung mit der veränderten Abtastschrittweite fortsetzen
 .
.
- Das Modell rechnet zu ungenau, so dass durch die Abtastschritte kein Anstieg auf der Gütefunktion erkannt werden kann (Numerisches Rauschen):
- Entwurfsparameter konvergiert gegen seinen Grenzwert:
- Falls der Grenzwert nicht infolge einer Forderung festgelegt wurde (z.B. max. Einbaumaß) oder nicht der Physik widerspricht (z.B. negative Einschaltzeiten), sollte man die Grenze des Entwurfsparameters ändern.
- Ein Rücksetzen und erneutes Starten der Optimierung führt dann mit großer Wahrscheinlichkeit zu einer besseren Lösung.
- Die Lösung verschlechtert sich konsequent:
- Es werden im Modell fehlerhafte Bewertungsgrößen berechnet oder
- es wurden die Forderungen der Aufgabenstellung fehlerhaft in Form der Restriktionen oder Gütekriterien definiert.
- Konvergenz zum Optimum vorzeitig beendet:
- Bleiben nach einer gewissen Zeit alle Nennwerte konstant, so kann man noch nicht sicher sein, wirklich ein Optimum erreicht zu haben.
- Im Beispiel wird die Zielfunktion um das Optimum so flach, dass aufgrund des numerischen Rauschens das Optimierungsverfahren keine Richtungsinformation mehr gewinnen kann.
- Man sollte in jedem Fall versuchen, eine Optimierung ausgehend von den gleichen Anfangswerten, mit einer höheren Rechengenauigkeit durchzuführen (absTol und relTol).
- Erreicht man damit den gleichen Bestwert, so handelt es sich mit großer Wahrscheinlichkeit um eine optimale Lösung.
- Ist dies nicht der Fall, kann man die Rechengenauigkeit weiter erhöhen (falls die Berechnungszeit dies noch zulässt!).