Software: SimX - Nadelantrieb - Robust-Optimierung - Grundlagen

↑

← →

Robust-Optimierung (Grundlagen)

Mit der Minimierung der Versagenswahrscheinlichkeit erreichten wir eine Lösung, welche auf den ersten Blick allen Forderungen genügen sollte. Doch da wir inzwischen nicht mehr "computergläubig" sind, sollten wir auch diese Ergebnisse einer tieferen Analyse unterziehen:

1. Modelle als vereinfachte Abbilder

• Es wurden nur die physikalischen Effekte im Modell berücksichtigt, die in Hinblick auf die Nutzung des Modells bisher als relevant eingeschätzt wurden.
• Abweichungen im zeitlichen Verlauf der Modellgrößen von ca. ±20% können für das Dynamik-Modell eines Elektromagneten als ziemlich genau gelten.
• Die berechneten Streuungen der Ausgangsgrößen in Abhängigkeit von den Parameter-Streuungen sind deshalb mit einem Fehler gleicher Größenordnung behaftet.

2. Vernachlässigung von Streuungen

• Aus Gründen der zeitlichen Machbarkeit ist es mit den jetzigen numerischen Methoden in den nächsten Jahren noch nicht möglich, die Streuungen aller Modellparameter bei der Simulation zu berücksichtigen.
• Die Reduktion der Simulation auf die Streuungen mit dem größten Einfluss auf die Bewertungsgrößen führt zu "geschönten" Ergebnissen in Hinblick auf die Versagenswahrscheinlichkeit.

3. Fehler bei probabilistischer Simulation

• Ungenaue Verteilungsfunktionen für die Streuungen infolge unzureichender Informationen zur Fertigung und zu den Einsatzbedingungen.
• Begrenzte Stichprobengröße bzw. Bildung vereinfachter Übertragungsfunktionen.
• Diese Ungenauigkeiten der Abbildung der Streuungen im probabilistischen Modell führen zu Unsicherheiten in Hinblick auf die Streuungen der Ausgangsgrößen.

4. Validierte Modelle sind tendenziell richtig

• Die Validierung muss zuvor für den angestrebten Nutzungsbereich des Modells erfolgt sein.
• Änderungen von Modellparametern bewirken dann eine qualitativ richtige Reaktion der Ausgangsgrößen.
• Damit korreliert eine Verbesserung des Modellverhaltens sehr stark mit einer Verbesserung des realen Objektverhaltens.

Aus diesen Feststellungen kann man für die optimale Lösung der Ausschuss-Minimierung schlussfolgern:

• Die zuverlässigkeitsbasierte optimierte Lösung wird innerhalb der Parameter-Streuungen besser funktionieren, als die Ausgangslösung ohne Berücksichtigung von Streuungen.
• Auf Grund der unvermeidlichen Ungenauigkeiten und Vereinfachungen ist es sehr wahrscheinlich, dass die Versagenswahrscheinlichkeit im praktischen Betrieb noch nicht bei Null liegt.
• Es wäre günstig, wenn man vor dem endgültigen Bau eines teuren Versuchsmusters die Wahrscheinlichkeit vergrößern könnte, dass man im praktischen Betrieb eine stabile und weitestgehend funktionsfähige Lösung erhält.

Robust-Optimierung ist ein Ansatz für eine weitere Verbesserung unserer optimierten Lösung:

• Streuungen der Modellparameter sollten nur zu einer kleinen Streuung der Ergebnisgrößen führen.
• Meist sind die Streuungen der Modellparameter durch die Herstellung und die Einsatzbedingungen bereits vorgegeben.
• Aufgabe der Robustoptimierung ist es, die Streuungen der Bewertungsgrößen bei vorgegebenen Parameter-Streuungen zu minimieren.
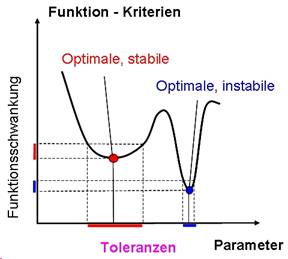
• Im nebenstehenden Bild wird versucht, den Unterschied zwischen einer instabilen und einer robusten Optimallösung zu verdeutlichen.

Die Streuungen der Bewertungsgrößen werden mathematisch über ihre Varianzen erfasst:

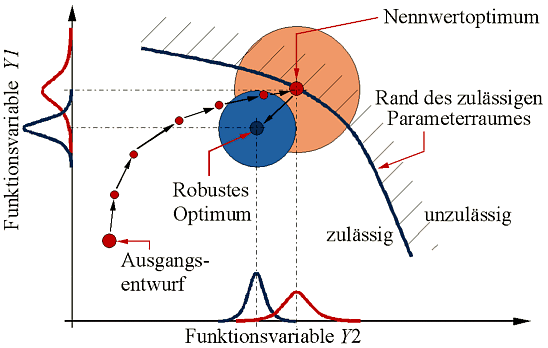
• Gesucht wird eine möglichst gut funktionierende Lösung, welche zusätzlich zur Ausschussquote=0 minimale Varianz-Werte für die wesentlichen Bewertungsgrößen aufweist.
• Es handelt sich praktisch um eine Ausschuss-Minimierung mit gleichzeitiger Minimierung der Varianzen der streuenden Bewertungsgrößen. D.h., der Streubereich der Lösung soll verkleinert werden.

Bei der Suche nach solch einer Lösung wird es mit großer Wahrscheinlichkeit zu Widersprüchen zwischen den einzelnen Bewertungsgrößen kommen! Erforderlich ist deshalb eine Mehrkriterien-Optimierung, welche die Entscheidungsgrundlage für eine angemessene Kompromisslösung liefert.

Mehrkriterien-Optimierung

• In der Entwicklung und Konstruktion von Produkten trifft man sehr häufig Optimierungsaufgaben mit mehreren Gütekriterien. Dabei wird ein Vektor von Entwurfsparametern gesucht, mit dem möglichst die Werte aller Gütekriterien minimiert werden (Mehrkriterien-Optimierung, auch Pareto-Optimierung genannt).
• Die Kriterien sind miteinander oft nicht verträglich. Beim Versuch die Werte einiger Kriterien zu minimieren, können sich die Werte anderer Kriterien vergrößern. Bei unserem E-Magneten führt z.B. eine Verkleinerung der Einbaulänge zu einer Erhöhung der Spulentemperatur. Auch eine Verringerung der Zykluszeit führt zu einer Temperaturerhöhung.
• Es gilt fast in jedem Fall: bessere Funktionserfüllung führt zu höheren Kosten.
• Es gibt keine eindeutige Lösung, sondern eine pareto-optimale Lösungsmenge:

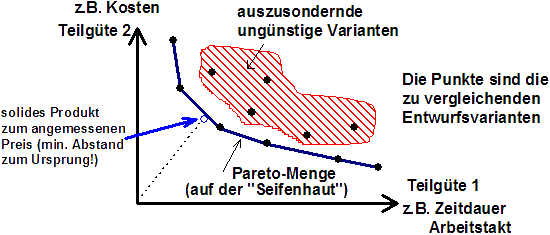
Dieses Pareto-Optimum (nach Vilfredo Pareto) ist dadurch gekennzeichnet, dass es nicht mehr möglich ist, eine Teilgüte zu verbessern, ohne gleichzeitig mindestens eine andere Teilgüte zu verschlechtern. In Abhängigkeit von den Verwertungsbedingungen kann der Nutzer dann eine Lösung aus der Pareto-Menge wählen, z.B.:

• Beste Funktionalität um jeden Preis.
• Ausgewogenes Preis-/Leistungsverhältnis.
• So billig wie möglich, solange es überhaupt funktioniert.

← →