Software: SimX - Nadelantrieb - Robust-Optimierung - Experimentkonfiguration

↑

← →

Robust-Optimierung (Experiment-Konfiguration)

Mehrkriterielle Robust-Optimierung

Wir wollen nun ausgehend vom Bestwert der Ausschuss-Minimierung eine robuste Lösung für unseren Antrieb suchen, die folgenden Kriterien möglichst gut genügt:

• Die Streubreite der Zykluszeit ist zu minimieren (Robustoptimierung).
• Ein Prägezyklus soll dabei möglichst schnell erfolgen (Mittelwert über eine Stichprobe).
• Die Spulenerwärmung soll möglichst gering sein (Mittelwert über eine Stichprobe).
• Die Streubreite der Spulenerwärmung ist funktionell von geringerer Bedeutung, solange die max. Erwärmung nicht markant überschritten wird. Deshalb streben wir im Rahmen dieser Robust-Optimierung keine Minimierung dieser Streuung an.
• Es handelt sich hierbei um eine Mehrkriterien-Optimierung, denn wir wollen drei unterschiedlichen Gütekriterien möglichst gut genügen. Zumindest die Ziele der Verringerung der Zykluszeit und der Spulenerwärmung widersprechen sich wahrscheinlich!

Als unmittelbares Ergebnis einer Mehrkriterien-Optimierung wird eine Pareto-Menge der optimalen Kompromisslösungen ermittelt:

• Wir erhalten als Entscheidungsgrundlage für die endgültige Lösungswahl einen Zusammenhang, in welchem Maße die Verbesserung einer Teilgüte zur Verschlechterung der anderen Teilgüten führt.
• Anhand dieser Pareto-Menge können wir bewerten, in welchem Maße die bisherige Ausschuss-minimierte Lösung noch im Sinne einer robusteren Lösung verbessert werden kann bzw. ob für den Einsatzzweck ein anderer Kompromiss zwischen sich widersprechenden Gütekriterien sinnvoll ist.
• Die gewählte endgültige Lösung muss dann alle aktuellen Forderungen (Restriktionen) innerhalb des Streubereichs der berücksichtigten Parameter-Streuungen einhalten.

Als wesentliche Streuungen berücksichtigen wir wie bei der Ausschuss-Minimierung:

• Unsicherheit des Wirbelstromwiderstands
• Fertigungstoleranzen der Rückholfeder
• Unterschiedliche Papiersorten

Hinweise:

• Wir nutzen das neue SimulationX-Modell Etappe6_xx_Robust.isx ebenfalls als Kopie der Datei Etappe5_xx_Nennwert.isx.
• Wir verwenden einen neuen OptiY-Versuchsstand Etappe6_xx_Robust.opy. Diese Datei erzeugen wir als Kopie aus der Datei Etappe6_xx_Ausschuss.opy.
• In dieser neuen Datei übernehmen wir den bei der Ausschuss-Optimierung erreichten Bestwert als Parameter und somit als Ausgangslösung für die Robust-Optimierung.
• Im Workflow wählen wir für das SimulationX-Modell die neue Datei Etappe6_xx_Robust.isx.
• Nach Rücksetzen des Projektes zum Löschen der veralteten Experimentdaten speichern wir Etappe6_xx_Robust.opy.

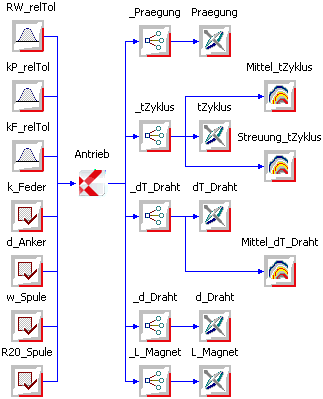
Für die Minimierung der Streuungen von tZyklus und dT_Draht benutzen wir im OptiY-Workflow die Standardabweichung "sigma". Ihr Wert repräsentiert direkt die Streubreite in der verwendeten Maßeinheit. Deshalb ist die Standardabweichung physikalisch einfacher zu interpretieren als der zugehörige Varianz-Wert:

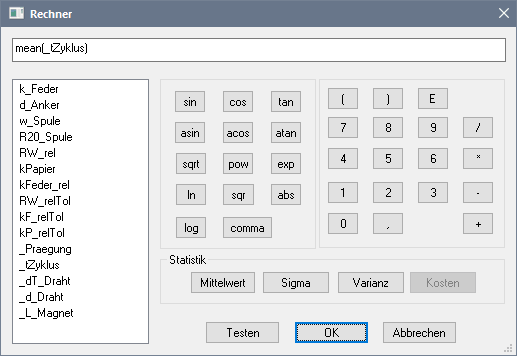
Zur Berechnung von Mittelwert bzw. Standardabweichung (Streuung) der Gütekriterien nutzen wir die Möglichkeiten des für das Bearbeiten der Eigenschaften bereitgestellten "Rechners", z.B.:

Statistische Versuchsplanung

In Hinblick auf die Wechselwirkungen zwischen den Parameter-Streuungen kann man im Beispiel annehmen, dass die gleichen Bedingungen gelten, wie bei der vorherigen Ausschuss-Minimierung. Wir können deshalb für die probabilistische Simulation der Stichproben wieder das Moment-Verfahren mit dem Polynomansatz 2. Ordnung ohne Berücksichtigung von Interaktionen verwenden.

Optimierungsverfahren

Im Vergleich zu unseren bisherigen Optimierungsexperimenten haben wir nun ganz andere Bedingungen in Hinblick auf die Gütekriterien:

• Bei Strafe und Versagen handelt es sich, wie bereits bekannt, um interne Gütekriterien innerhalb der hierarchischen Optimierungsstrategie.
• Jedoch sollen nun insgesamt drei "echte" Gütekriterien möglichst gleichzeitig in Hinblick auf ihre Werte minimiert werden!
• Es ist sehr wahrscheinlich, dass es dabei zu Widersprüchen kommt und man sich letztendlich für eine Kompromisslösung entscheiden muss.
• Grundlage für diese Entscheidungsfindung ist die Pareto-Menge.
• Das Hypervolumen als ein weiteres internes Gütekriterium wird bei mehr als zwei "echten" Gütekriterien hinzugefügt:
  • Dieser Hypervolumen-Indikator (HVI) wird zur Qualitätsbewertung von Pareto-Front Approximationsmengen in der Mehrkriterien-Optimierung eingesetzt.
  • Über den HVI-Wert wird die Konvergenz der Lösungen in Richtung auf die Pareto-Menge gesteuert.
• Diese Pareto-Lösungsmenge kann in OptiY nur bei Verwendung Evolutionärer Algorithmen (Evolutionsstrategie) generiert werden:

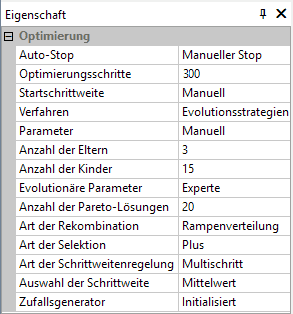
• Für das Optimierungsproblem werden wir die Werte aus den Standardeinstellungen etwas modifizieren. Dazu müssen wir eine Umschaltung von "Standard" auf "Manuell" bzw. "Experte" vornehmen:
  • Wir arbeiten mit 3 Eltern, die gemeinsam in jeder Generation 15 Kinder durch Multirekombination erzeugen. Die Erhöhung der Elternzahl soll eine gewisse Glättung auf der etwas verrauschten Zielfunktion bewirken. Um den Selektionsdruck zu erhalten, musste die Kinderzahl entsprechend erhöht werden.
  • Die Eltern konkurrieren gemeinsam mit ihren Kindern darum, in der nächsten Generation wieder zu den 3 Eltern zu gehören (Selektion=Plus).
  • Die Anpassung der Mutationsschrittweite an die Zielfunktion erfolgt getrennt für jede Entwurfsgröße (Schrittweitenregelung=Multischritt).
  • Die Anzahl der Optimierungsschritte=300 beschreibt für das Optimierungsverfahren die Gesamtzahl der zu berechnenden Kinder. Man beachte, dass bei der zuverlässigkeitsbasierten Optimierung jedes "Kind" eine probabilistische Simulation einer Stichprobe darstellt, die mehrere (hier 7) Modell-Läufe benötigt!
  • Die Anzahl der Pareto-Lösungen ist eine interne Steuergröße für die Co-evolutionären Prinzipien bei der Mehrkriterien-Optimierung. Dieser Wert=20 ist unabhängig von der Größe der Pareto-Menge, welche man für die Darstellung in Diagrammen festlegen kann!

Hinweis: Das Gütekriterium "Hypervolumen" erscheint erst im Experiment-Browser nach Wahl von "Evolutionsstrategien" als Optimierungsverfahren. Allerdings nur, wenn man im geöffneten Workflow irgendein Objekt anklickt oder die Datei nach dem Speichern wieder geöffnet wird (Darstellungsfehler?).

Entwurfsparameter (Nennwerte und Streuungen)

Die Lösung der Robust-Optimierung kann sich von dem Ergebnis der Ausschuss-Minimierung unterscheiden. Das wird jedoch durch die zusätzlichen Gütekriterien gesteuert. Die Einstellungen für die Entwurfsparameter können wir fast unverändert von der Ausschuss-Minimierung übernehmen:

• Die Startwerte der Nennwerte müssen dem Bestwert aus der Ausschuss-Minimierung entsprechen.
• Die Startschrittweiten dienen nun als Maß für die Mutation.
• Als Grenzen für den Suchraum haben sich folgende Werte als günstig erwiesen, um z.B. negative Parameterwerte infolge "wilder" Schwingungen zu erschweren:

d_Anker   : 6...15 mm 
w_Spule   : 200...1000 
R20_Spule : 0.1...10 Ohm
k_Feder   : 10...100 N/mm 

Die Streuungen besitzen die gleichen vorgegebenen, konstanten Werte, wie bei der Ausschuss-Minimierung:

d_Papier  : Nennwert=0,2 mm  / Toleranz=0,2 mm      / Gleichverteilung (verschiedene Papiersorten)
Re_Eisen  : Nennwert=1,5 mΩ  / Toleranz=1,5 mΩ      / Normalverteilung 
kFeder_rel: Nennwert=1       / Toleranz=0,6         / Normalverteilung (±30% um normierten Nennwert)

Restriktionen

In Hinblick auf die Benutzung von Restriktionen müssen wir bei der mehrkriteriellen Optimierung umdenken, denn es wirkt nun eine erweiterte Zielfunktionshierarchie:

1. Einhaltung des Suchraums (Grenzen der variablen Entwurfsparameter)
2. Einhaltung aller Forderungen (Restriktionen) für die Nennwerte der Stichprobe (Strafe=0)
3. Einhaltung aller Forderungen (Restriktionen) für die gesamte Streuung der Stichprobe (Versagen=0)
4. Erfüllung der Wünsche (benutzereigene Gütekriterien)

Wenn wir alle Forderungen der Aufgabenstellung weiterhin als wirksame Restriktionen definieren, kommt die Optimierung mit Sicherheit kaum zur Bearbeitung der eigentlich interessierenden letzten Zielfunktion:

• Bereits bei der Ausschuss-Minimierung mussten wir uns bemühen, Restriktionsverletzungen für die Nennwerte der Stichproben weitestgehend zu reduzieren. Als besonders kritisch erwies sich hier eine Konvergenz der Lösung entlang von Restriktionsgrenzen. Durch geschicktes "Ansteuern" eines verfügbaren Drahtdurchmessers und eventueller Freigabe der Magnetlänge konnten wir mit viel Kreativität diese Hürde (hoffentlich) überwinden.
• Nun müssen wir dafür Sorge tragen, ein Versagen>0 von Stichproben bei der Ermittlung der pareto-optimalen Lösungsmenge möglichst zu vermeiden:

1. Die Gütekriterien sind so zu definieren, dass sie tendenziell die zugehörigen Forderungen der Aufgabenstellungen übererfüllen. Dies gilt im Beispiel für das Minimieren der Zykluszeit genauso, wie für das Minimieren der Drahterwärmung. Restriktionen, für welche solche Gütekriterien definiert wurden, müssen deshalb durch Aufweiten ihrer Grenzen unwirksam gemacht werden (unwirksame Grenzen für tZyklus, dT_Draht sowie für B_max und i_Max).
2. Falls im Sinne von Versagen>0 noch kritische Restriktionen existieren, sollte man überlegen, ob diese durch Definition geeigneter Gütekriterien eliminiert werden können. Im Beispiel betrifft dies die unstetige Größe Praegung, welche zu einem Teilversagen einer Stichprobe führen kann. Da dies jedoch nur sporadisch auftritt, wird dadurch die Pareto-Optimierung nur unwesentlich behindert. Wir benötigen dafür kein weiteres Gütekriterium, müssen die Restriktion aber beibehalten (Praegung=0.85...1.3).
3. Forderungen der Aufgabenstellung, welche kritisch im Sinne von Strafe>0 sind, behandeln wir wie bei der Ausschuss-Minimierung. Die Magnet-Länge begrenzen wir nun nicht mehr, da ein eventuell etwas größerer Bauraum realisierbar ist. Den Drahtdurchmesser berücksichtigen wir vorläufig nicht (unwirksame Grenzen für L_Magnet und d_Draht).

← →