Software: SimX - Nadelantrieb - Robust-Optimierung - Ergebnisse
Experiment-Durchfuehrung
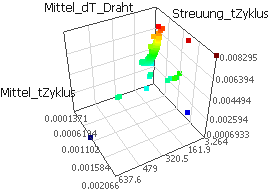
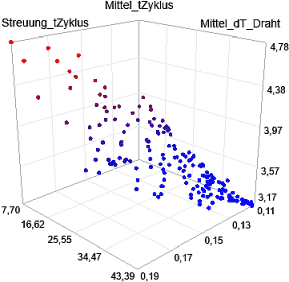
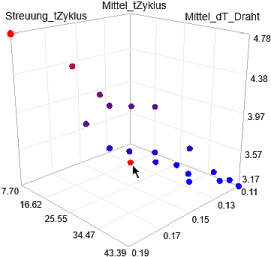
Da wir nur drei Gütekriterien berücksichtigen, können wir die Lösungen noch komplett in einer 3D-Darstellung als "Kriterien-Raum" visualisieren (Analyse > Darstellung > 3D-Darstellung). Die Achsen belegen wir mit unseren Gütekriterien, wobei es sinnvoll ist, die mittlere Zykluszeit als funktionelle Größe auf die Z-Achse zu legen:
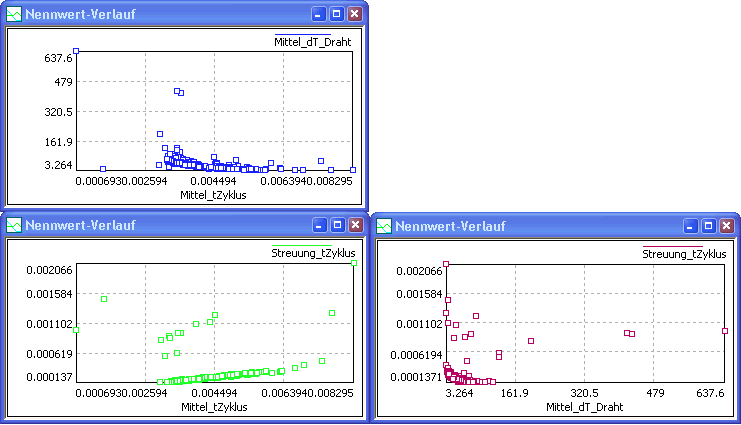
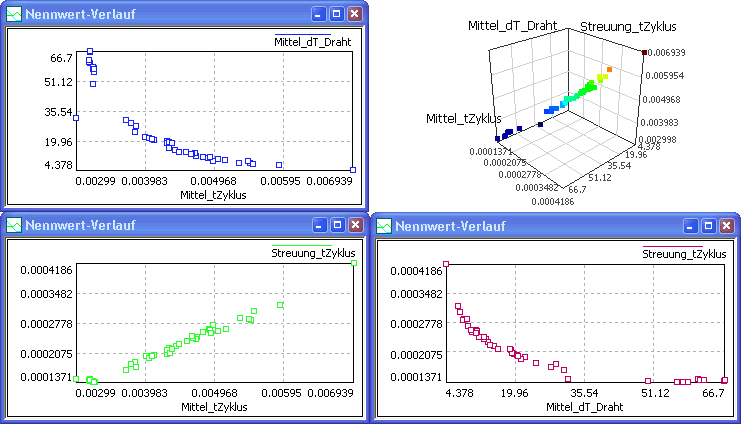
Zusätzlich ist es sinnvoll, möglichst alle Abhängigkeiten zwischen den Gütekriterien als 2D-Darstellung im Sinne von Projektionen des mehrdimensionalen Kriterien-Raumes abzubilden:
- Dazu stellt man jeweils zwei Kriterien in einem Nennwert-Fenster dar und schaltet danach unter Analyse > Darstellung auf 2D-Darstellung um (ein Kriterium muss dabei zuvor im Nennwert-Fenster als X-Achse selektiert sein!).
- Die 2D-Diagramme muss man dann auch noch so konfigurieren, dass nur die Lösungspunkte dargestellt werden.
- Im Beispiel ergibt das drei Projektionen der Lösungsmenge entsprechend der Anzahl möglicher Paar-Kombinationen:
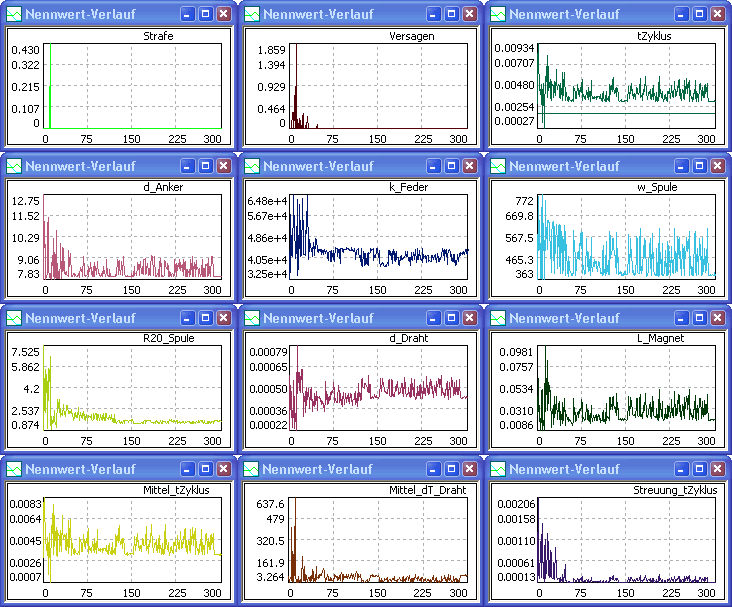
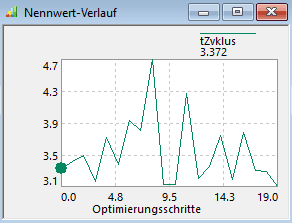
Die einzelnen Lösungspunkte repräsentieren jeweils eine Stichprobe, die im Rahmen der co-evolutionären Optimierungsstrategie berechnet wird. Der Verlauf der Co-Evolution widerspiegelt sich in den Nennwert-Diagrammen der variablen Entwurfsparameter und der Bewertungsgrößen des Experiments:
- Im Beispiel entsprechen 15 Stichproben (Kinder) jeweils einer Generation innerhalb der Evolutionsstrategie.
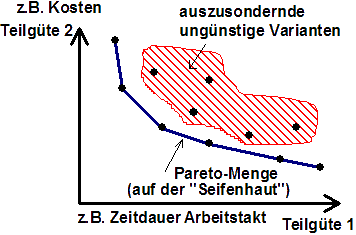
- Der längerfristigen evolutionären Entwicklung der Population sind die Mutationen der einzelnen Individuen überlagert.
- Die Population bewegt sich infolge der Evolutionsstrategie zuerst in den Bereich zulässiger Nennwert-Lösungen (Strafe=0).
- Danach entwickelt sich die Population weiter in Richtung minimalen Versagens innerhalb der Streuungen um die Nennwertlösungen (Versagen→0).
- Über den Hypervolumen-Indikator-Wert wird danach die Konvergenz der Lösungen in Richtung auf die Pareto-Menge gesteuert. Bildlich gesehen bewegt sich die Population zum Bereich der pareto-optimalen Lösungsmenge.
- Infolge der zusätzlich unterlegten co-evolutionären Strategie oszilliert die Population dann bei Versagen=0 endlos auf der pareto-optimalen Lösungsmenge.
- Durch die Mutationen entstehen auch einzelne "Ausreißer", welche im Normalfall zu sehr schlechten Lösungen führen. Gleichzeitig bieten diese Fluktuationen aber auch die Chance für größere Sprünge innerhalb des Suchraumes und damit dem Erreichen neuer "ökologischer Nischen".
Experiment-Auswertung
Bisher werden in den 2D/3D-Diagrammen für jeden Optimierungsschritt (entspricht jeweils einer berechneten Generation) die Nennwerte des jeweils "besten" Exemplars dargestellt. Diese Darstellung der kompletten "Optimierungsmenge" ist durch die Vielzahl von "schlechten Lösungen" (insbesondere durch die Ausreißer) sehr unübersichtlich. Uns interessieren nur die Mitglieder der Pareto-Menge:
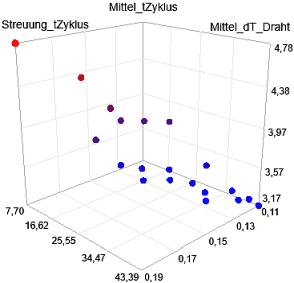
Nach Wahl der "Pareto-optimalen Menge" bleiben nur die zulässigen Lösungen auf der "Seifenhaut" in den Diagrammen erhalten:
Die 2D-Projektionen dieser "Seifenhaut"-Menge führt im Beispiel nur für die (Mittel_tZyklus, Mittel_dT_Draht)-Ebene zu einer anschaulichen Darstellung der Pareto-Menge:
Die anderen beiden Projektionen resultieren aus der ungünstigen Blickrichtung auf die Lösungspunkte der "Seifenhaut".
Die berechneten Lösungspunkte sind auf der "Seifenhaut" ungleich verteilt. Um eine Entscheidung in Hinblick auf die beste Kompromisslösung zu erleichtern, ist es günstig die Anzahl der dargestellten Lösungspunkte auszudünnen. Diese Filterung sollte so erfolgen, dass eine vorgegebene Anzahl von Lösungspunkten übrigbleibt, welche gleichmäßig auf der Seifenhaut verteilt ist und die beste Kompromisslösung enthält:
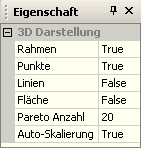
- Man wählt Analyse > Menge-Auswahl > Gefilterte Pareto-Menge.
- Standardmäßig enthält die gefilterte Pareto-Menge nur 10 Lösungen.
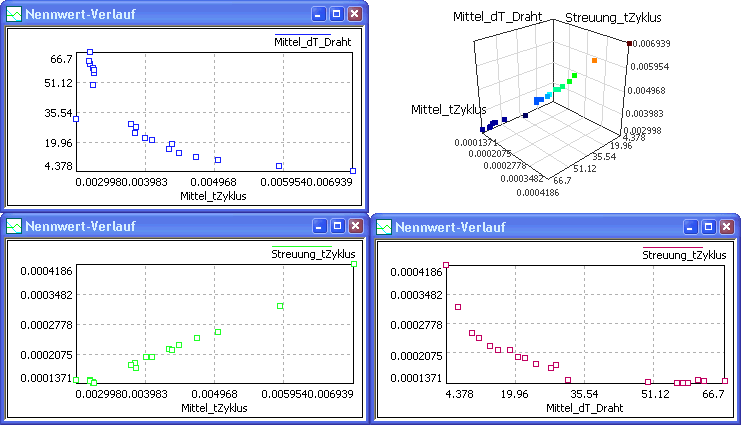
- Wir erhöhen die Anzahl der Lösungen in der Pareto-Menge, indem wir in einem der Fenster-Eigenschaften diesen Wert=20 setzen. Der neue Wert wird dann für alle Fenster übernommen und die gefilterte Pareto-Menge wird neu berechnet. Die Lösungspunkte dieser gefilterten Pareto-Menge verteilen sich gleichmäßig auf der Pareto-Schale, weil dicht beieinander liegende Lösungen und Ausreißer herausgefiltert werden:
- Nach der Filterung sind die noch vorhandenen 20 Lösungspunkte auch in den 2D-Darstellungen einzeln erkennbar:
- Hinweis: Leider bleibt nach einem Speichern und neu Öffnen der .opy-Datei die Darstellung der gefilterten Pareto-Menge in den Diagrammen nicht erhalten (Kurzzeitiges Umschalten in der Mengenauswahl ist erforderlich!).
Die Aufgabe besteht nun darin, aus der dargestellten gefilterten Pareto-Menge eine günstige Kompromisslösung auszuwählen:
- In jedem der 2D-Diagramm kann man einen der zu analysierenden Lösungspunkte mit dem Cursor auswählen. Die ausgewählte Lösung erscheint dann in allen 2D- und auch den 3D-Diagrammen als markiert.
- Zuerst sollte (wie gezeigt) der Bestwert aus der Ausschuss-Minimierung ausgewählt werden, um seine Position in Hinblick auf die Pareto-Menge einschätzen zu können. Dieses Ausschuss-Minimum war der Startwert unserer Robust-Optimierung (Optimierungsschritt=0) und sollte in der gefilterten Pareto-Menge enthalten sein. Die Auswahl kann günstiger Weise im Nennwert-Verlauf der Zykluszeit erfolgen (Pfeil zeigt auf zugehörigem Lösungspunkt im 3D-Diagramm):
- Hinweis: Ist das Ausschuss-Minimum wider Erwarten nicht enthalten, so muss man zur Beurteilung seiner Lage die Mengenauswahl wieder auf die Pareto-Menge oder sogar auf die komplette Optimierungsmenge zurücksetzen!
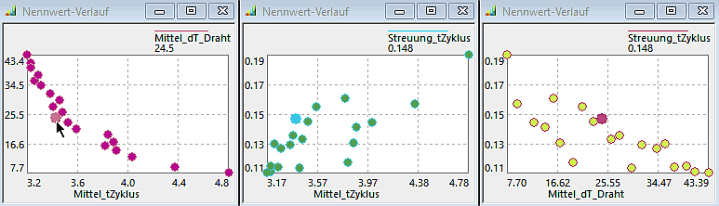
- In den 2D-Diagrammen ist das gewählte Ausschuss-Minimum links mit einem Pfeil markiert und hebt sich in den folgenden Diagrammen farblich gut ab:
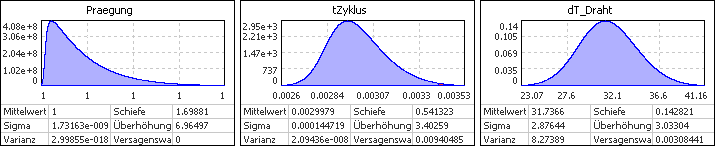
- Um eine ausgewählte Lösung analysieren zu können, sollte man die Verteilungsdichte-Diagramme der Restriktionsgrößen darstellen, welche zu den Gütekriterien gehören. Nach Auswahl eines Lösungspunktes werden in diesen Diagrammen die Verteilungsdichten der Lösung dargestellt:
Wichtig: Damit die Teilversagenswahrscheinlichkeiten in Verteilungsdichte-Diagrammen angezeigt werden können, müssen zuvor die Restriktionsgrenzen für die Zykluszeit und die Spulenerwärmung wieder auf den geforderten Wert gesetzt werden!
Auf Grundlage der Pareto-Menge kann man entscheiden, wieviel Verschlechterung einzelner Gütekriterien man akzeptiert, um anderen Kriterien möglichst gut zu genügen:
- Der Hauptwiderspruch zwischen möglichst schneller Zykluszeit und minimaler Erwärmung ist im linken 2D-Diagramm deutlich erkennbar → je schneller der Magnetantrieb, desto größer ist die Erwärmung der Spule.
- Man wird sich in diesem Diagramm für einen Antrieb entscheiden, der möglichst schnell ist und sich trotzdem noch nicht so stark erwärmt.
- Die Streuungen der Zykluszeit und der Spulentemperatur spielen keine wesentliche Rolle, weil diese für die Lösungen der Paretomenge bereits minimiert sind.
- Der bereits ausgewählte Bestwert aus der Ausschuss-Minimierung stellt im Beispiel anscheinend schon einen sehr guten Kompromiss dar.
- Der Vorteil dieser Lösung besteht darin, dass sie bereits auf einem Norm-Drahtdurchmesser benutzt!
Problem des Drahtdurchmessers:
- Während der Ausschuss-Minimierung war es noch problemlos möglich, einen genormten Drahtdurchmesser mit Hilfe der entsprechenden Restriktionsgröße zu erzwingen.
- Bei der multikriteriellen Robustoptimierung scheitert die co-evolutionäre Strategie mit großer Wahrscheinlichkeit an den zusätzlich erforderlichen, sehr engen Draht-Restriktionen. Eine Oszillation der Lösung entlang der Pareto-Menge kommt dann nicht zustande!
- Wenn die erreichte Optimal-Lösung der Ausschuss-Minimierung beibehalten werden kann, gibt es das Problem des Drahtdurchmessers bei der multikriteriellen Robustoptimierung nicht mehr.
- Man erhält dann mit der multikriteriellen Robustoptimierung nur noch die Bestätigung, dass man bereits über eine optimale Kompromisslösung verfügt.
- Falls sich wider Erwarten andere Lösungen als optimale Kompromisslösungen erweisen, so kann man versuchen, eine Lösung zu wählen, welche näherungsweise einen Normdraht enthält. Durch vorherige Wahl einer größeren Pareto-Anzahl (z.B. 40) stehen dafür mehr Lösungspunkte zur Verfügung:
- Man findet im Beispiel zwar Lösungen mit etwas kürzeren Zykluszeiten bei dünnerem Draht, aber wie schon aus der Ausschuss-Minimierung bekannt, wird dabei die Spule wesentlich wärmer.
- Da der verfügbare Draht mit 0,5 mm noch etwas dünner ist, als in den Lösungen mit 0,51 mm, würde sich die Temperatur noch erhöhen.
- Zumindest im gezeigten Beispiel findet man keine bessere Kompromiss-Lösung als den Bestwert aus der Ausschuss-Minimierung.
Experiment-Ergebnisse (Robust-Optimierung)
Falls die optimale Lösung der Ausschuss-Minimierung nicht bestätigt werden konnte, wird man sich für eine bessere Lösung entscheiden. Die Wahl dieser Lösung ist zu begründen!
Mit welchen technisch sinnvollen Nennwerten ergibt sich dann (ohne Berücksichtigung von Normdrähten) eine robuste und trotzdem schnelle Antriebslösung mit möglichst geringer Ausschuss-Quote:
- d_Anker (Ankerdurchmesser)
- L_Magnet (Magnetlänge ohne Restriktion!)
- R20_Spule (Widerstand der Spule bei 20°C)
- w_Spule (Windungszahl)
- d_Draht (aus Normreihe)
- Feder.k (Elastizitätskonstante)
- Feder.s0 (Vorspannweg)
- t_Zyklus (Mittelwert sowie min. und max. auftretende Werte → Grenzwerte von 6σ)
Wichtig:
- Als Bestandteil der Lösung muss die gespeicherte .opy-Datei der Robust-Optimierung die Optimierungsergebnisse in den erläuterten Diagrammen in anschaulicher Form enthalten.
- Das zugehörige SimulationX-Modell ist mit den Nennwert-Parametern für die gefundene optimale Lösung zu konfigurieren. Der simulierte Verlauf des Prägezyklusses ist in anschaulicher Form in einem Ergebnisfenster darzustellen. Überflüssige Ergebnisfenster sind zu löschen!