Software: SimX - Nadelantrieb - Aktordynamik - Wirbelstrom-Modell

↑

← →

Wirbelstrom-Modell

Vorbereitung des neuen Bearbeitungsabschnittes (B)

Die geöffnete Modell-Datei Etappe2a_xx.isx sollte mit der ermittelten Bestwerten konfiguriert und gespeichert sein:

• In der Etappe2a_xx berücksichtigten wir nur die nichtlineare Funktion µ(B) für die Neukurve der BH-Kennlinie.
• Bevor wir mit dem Ergänzen des Wirbelstrom-Effektes fortfahren, erzeugen wir dafür eine weitere Modelldatei.
• Dazu speichern wir die geöffnete Modell-Datei Etappe2a_xx.isx unter dem Dateinamen Etappe2b_xx.isx:
  • Datei > Speichern unter im bisher für Etappe2 genutzten Ordner.
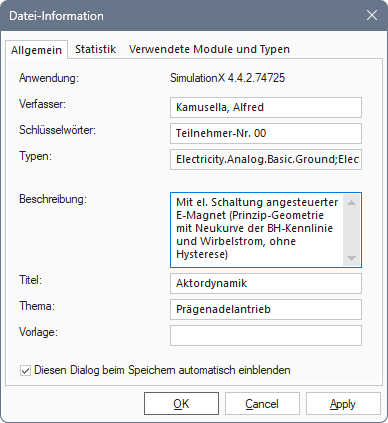
  • Die Datei-Informationen passen wir entsprechend der neuen Zielstellung an, z.B.:
    
  • Wichtig: Der Eintrag zur individuellen Teilnehmer-Nr. xx im Feld "Schlüsselwörter" darf nicht verändert werden!

Nach dem Speichern steht das Modell unter dem neuen Namen Etappe2b_xx zur weiteren Bearbeitung im SimulationX bereit.

Einfrieren der Signalverläufe:

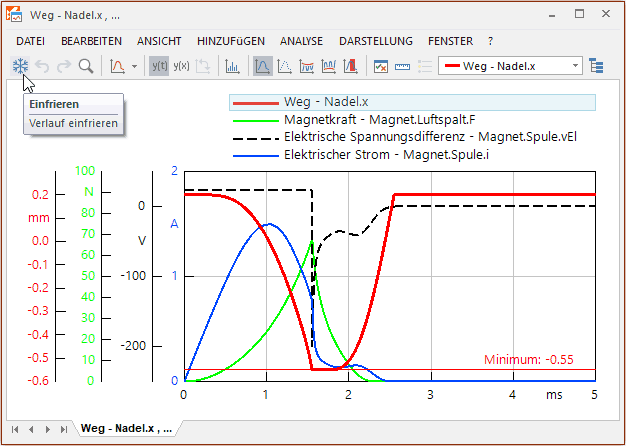
• Die aktuellen Signalverläufe im Ergebnisfenster widerspiegeln das bestmögliche Modellverhalten bei Berücksichtigung der µ(B)-Funktion für das Eisenmaterial.
• Da die Verläufe etwas eckig sind, verringern wir die min. Ausgabeschrittweite auf dtProtMin=(tStop-tStart)/1000, um verrundete Details hinreichend genau darzustellen.
• Zur Aktualisierung der Signalverläufe müssen wir die Simulation zurücksetzen und erneut starten.
• Damit wir das Verhalten mit den Bestwerten bei Berücksichtigung von Wirbelstrom und später auch noch der Hysterese vergleichen können, frieren wir diese Signalverläufe ein:
  

Vorbetrachtung

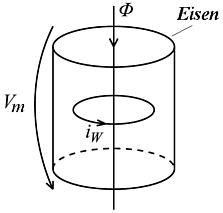
Wirbelströme entstehen durch Induktionsspannungen in elektrisch leitfähigen Materialien bei zeitlicher Änderung des sie durchdringenden magnetischen Flusses. Aus den Wirbelströmen resultiert entsprechend der Lenzschen Regel ein magnetisches Gegenfeld, welches das erzeugende Feld abschwächt:

• Infolge dieser Gegenwirkung wird die Feldänderung im Magnetkreis verzögert. Damit bewirken die Wirbelströme eine Ein- und Ausschaltverzögerung bei elektro-magnetischen Aktoren.
• Insbesondere bei schnellen Feldänderungen kommt es zu einer Feldverdrängung im Eisen. Dadurch verringert sich die effektiv durchströmte Fläche, was den magnetischen Widerstand der Eisen-Elemente in Abhängigkeit von der Feldänderungsgeschwindigkeit erhöht.
• Die Wirbelströme bewirken über die ohmschen Verluste entlang ihrer Bahn eine Erwärmung des Eisenmaterials. Insbesondere beim Einschaltvorgang bilden sie eine wesentliche Komponente der Eisenverluste.

Mit sehr großem Berechnungsaufwand kann man mittels Finite-Element-Simulationen die Wirkung der Wirbelströme innerhalb eines Magnetkreises detailliert untersuchen. Das ist innerhalb der System-Simulation mit Netzwerk-Modellen nur sehr eingeschränkt möglich!

Wir beschränken uns deshalb im Folgenden auf eine qualitative Nachbildung der Verzögerung der Feldänderung im Magnetkreis und die Auswirkung der Wirbelströme auf den Spulenstrom:

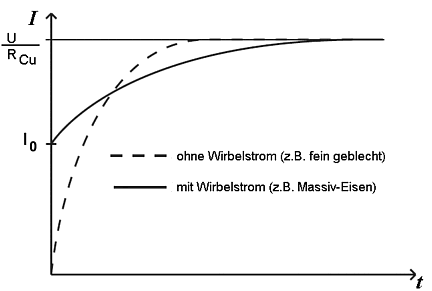
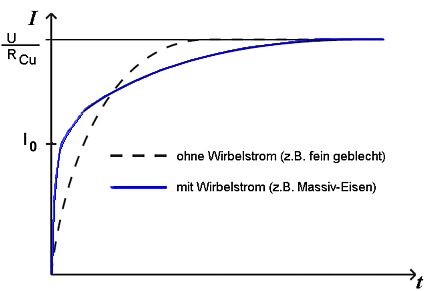
• Eine Messung des zeitlichen Verlaufs des Einschaltstroms an einem unbeweglichen Elektromagneten ergibt ohne Berücksichtigung der aussteuerabhängigen Permeabilität qualitativ folgende Stromverläufe:
  
• Der Endstrom I_end wird bestimmt durch die verwendete Betriebsspannung U und dem ohmschen Widerstand R_Cu des Spulendrahtes.
• Der Stromsprung I₀ resultiert aus dem praktisch sofort fließenden Wirbelstrom mit seinen ohmschen Verlusten in den Eisen-Elementen. Diese Verlustenergie EW=U·I₀ wird von der Spannungsquelle sofort bereitgestellt.
• Der Wert von I₀ liegt bei realen Magneten bezogen auf I_end bei maximal 5 bis 10%, wenn der Magnetkreis massive Eisenabschnitte enthält. Verwendet man geblechte Eisenkreise, so liegt dieser Sprung unter 1% und ist im Mess-Signal häufig kaum erkennbar.

Wir werden unser Modell nun so umgestalten, dass wir den Wirbelstrom zumindest in einer ersten Näherung berücksichtigen.

Globaler Wirbelstrom-Ersatzwiderstand

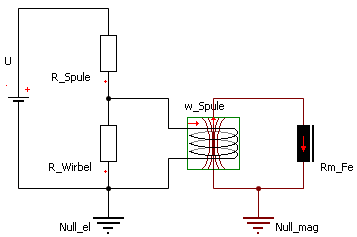
Die einfachste Methode (welche wir nicht anwenden!), ist die Berücksichtigung des Wirbelstroms durch einen ohmschen Widerstand auf der elektrischen Seite des elektro-magnetischen Wandlers (Spule):

• Dieser ohmsche Widerstand R_Wirbel muss direkt parallel zu den widerstandslosen Windungen der Spule angeordnet werden. Dazu müsste man im SimulationX-Spulenelement Rel=0 setzen!
• Der ohmsche Widerstand R_Spule des Windungsdrahtes liegt dann als separates Element in Reihe zur Spannungsquelle.
• Besitzt man infolge von Messungen (oder aus Erfahrung) den Wert I₀ für den Stromsprung und kennt den Endwert I_end, so kann man daraus R_Wirbel berechnen:
  R_Wirbel = R_Spule·(I_end/I₀ - 1)
• Beim Einschalten des Magneten kommt es mit diesem Modell zum Stromsprung I₀ und zu einer geringfügigen Verzögerung des Anzugsvorgangs, da an den Windungen der Spule weniger von der Betriebsspannung ankommt.
• Beim Abschalten ergibt sich die größte Auswirkung, indem der Abfallvorgang verzögert stattfindet. Der Wirbelstromwiderstand wirkt wie ein relativ kleiner Schutzwiderstand zur Begrenzung der Abschaltspannung. Dadurch benötigt der Abbau des Stromes eine längere Zeit und die Haltekraft bleibt länger erhalten!

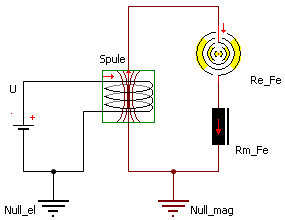
Die Wirkung dieses globalen elektrischen Ersatzwiderstandes kann man auch auf die magnetische Seite des elektro-magnetischen Wandlers transformieren:

Rel_Fe = R_Wirbel/w_Spule²

• Dieses Wirbelstrom-Element in der magnetischen Domäne entspricht einer Kurzschlusswindung um das zugehörige Eisen-Element Rm_Fe. Infolge der Flussänderungen im Eisen wird eine Spannung in dieser kurzgeschlossenen Windung induziert. Der ohmsche Widerstand entlang des sich ergebenden Strompfades bestimmt den Betrag des Wirbelstroms:
  
• Verwendet man obige Umrechnungsformel zwischen R_Wirbel und Re_Fe, so ist das Verhalten beider Modelle identisch:
  
• Das SimulationX-Spulenelement enthält nun wieder Windungszahl und ohmschen Widerstand des Drahtes.

Lokaler Wirbelstrom in jedem Eisen-Element

Auch die folgenden Betrachtungen führen wir noch ohne Veränderung unseres Modells durch:

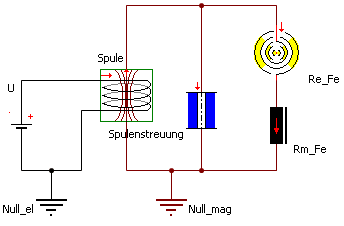
• Enthält die Netzwerk-Struktur der magnetischen Domäne Verzweigungen des magnetischen Flusses, so beeinflussen die Wirbelströme entscheidend die Aufteilung des magnetischen Flusses. Das kann man sich sehr einfach bei Berücksichtigung des Spulenstreufeldes verdeutlichen:
  
• Das Streufeld der Spule ist ein Luftelement und besitzt unabhängig vom aktuellen Magnetfeld einen konstanten magnetischen Widerstand.
• Der äußere Eisenabschnitt liegt in der Modellstruktur parallel zum Spulen-Streufeld. Bei schnellen Flussänderungen bewirkt das Wirbelstrom-Element ein Vergrößern des magnetischen Widerstandes des Eisen-Flusszweiges. Der magnetische Fluss wird damit durch das Streufeld der Spule "gedrückt" und geht damit dem eigentlichen Arbeitskreis für diese Zeitspanne verloren.

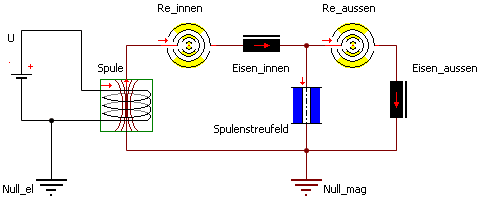
Wir betrachten nun unsere Netzwerk-Struktur. Infolge der Teilung des Eisenkreises in ein "inneres" und ein "äußeres" Eisen-Element kommt es zu weiteren Auswirkungen des Wirbelstroms, wenn wir diesen in beiden Eisen-Elementen berücksichtigen:

Der Einschaltstromsprung wird verschliffen, sodass der Wert I₀ nicht eindeutig ablesbar ist:

Modell-Erweiterung (Wirbelstrom)

CAD-Daten

Der Wert des elektrischen Widerstands der Wirbelstrom-Bahn eines jeden Eisen-Abschnitts wird durch Geometrie und Material-Eigenschaften des Eisenkreises bestimmt. Prinzipiell könnte man die Parameter für Wirbelstrom-Elemente aus den Abmessungen und den Material-Kennwerten berechnen. Bisher wurden in der Literatur jedoch noch keine praktikablen Berechnungen zum Erreichen dieses Ziels gefunden. Deshalb wird hier ein sehr einfacher Ansatz gewählt:

• Wir gehen von der konstruktiven Randbedingung aus, dass der gesamte Eisenkreis aus gleichem Material besteht.
• Der Querschnitt entlang des magnetischen Flusses soll im gesamten Eisenkreis näherungsweise gleich groß bleiben. Wir nehmen vorläufig an, dass auch die geometrische Form des Querschnitts gleich bleibt, da die konkrete Geometrie des Magnetkreises noch unbekannt ist.
• Mit diesen Annahmen ist der elektrische Leitwert der effektiven Wirbelstrombahn eines Eisenelements nur noch proportional zu seiner Länge.
• Wir geben für die gesamte Eisenlänge einen Wirbelstromwiderstand Re_Eisen als Parameter vor. Den Wert dieses gesamten Wirbelstromwiderstandes legen wir so fest, dass der Stromsprung beim Einschalten vorhandene Messungen oder Erfahrungswerte widerspiegelt.
• Bei der Parameter-Definition wählen wir einen Standardwert Re_Eisen = 1000 Ohm → Eisenmaterial praktisch ohne Wirbelstrom!
• Für einen Eisenabschnitt Fe_i des Magnetkreises kann man den zugehörigen Wirbelstromwiderstand auf Grundlage seines Anteils an der Gesamtlänge berechnen:
  Re_Fe_i=Re_Eisen·L_Eisen / L_Fe_i
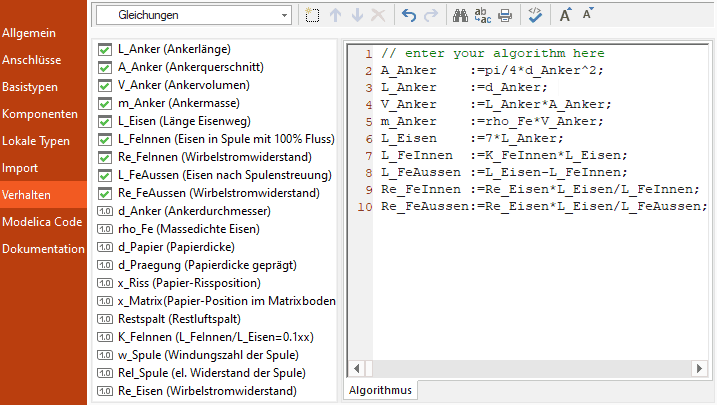
• Im CAD_Data-Compound werden die Zusammenhänge wie folgt berücksichtigt:
  

Wir konzentrieren alle weiteren Dimensionierungsberechnungen im CAD_Data-Compound, wie wir es bereits für einige Aspekte begonnen haben:

1. Alle für die Dimensionierung benötigten Größen werden als Parameter bzw. Variable im Komponenten-Abschnitt definiert.
2. Die im CAD-Element definierten Größen stehen dann anderen Modell-Elementen als Parameter zu Verfügung.

Modell-Struktur im Elektromagnet-Compound

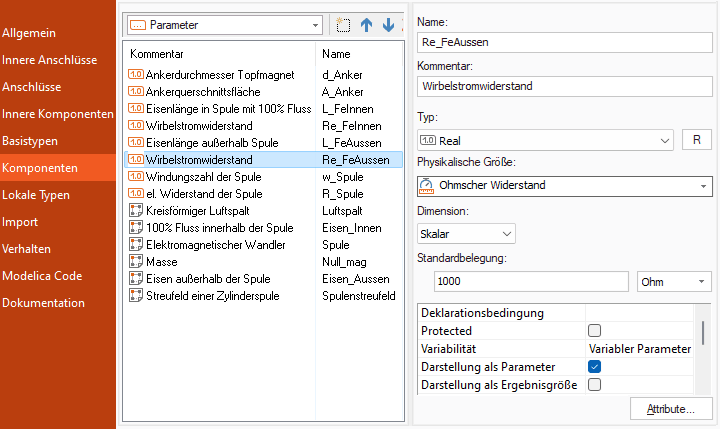
Bevor wir die interne Modellstruktur des Elektromagnet-Compound erweitern, ergänzen wir im Komponenten-Abschnitt dieses Compounds die Parameter Re_FeInnen und Re_FeAussen für die Wirbelstrom-Elemente:

• Der große Standardwert von 1000 Ohm bewirkt praktisch unwirksame Wirbelströme im Eisenmaterial.
• Vor dem Öffnen und Erweitern der Compound-Struktur muss man die Änderungen im TypeDesigner Fertigstellen und sollte die Modelldatei speichern:

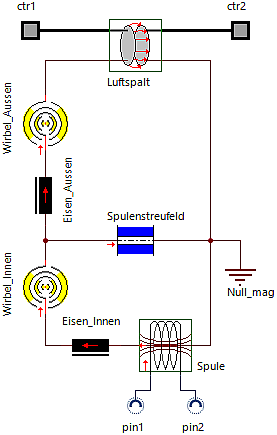
Wir benutzen den Wirbelstrom-Elementtyp aus der Bibliothek (Flussrichtung beim Einbinden berücksichtigen!):

Parameter-Konfiguration und Anfangswert-Fixierungen:

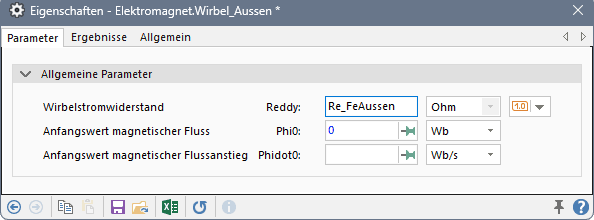
• Der Wirbelstromwiderstand Reddy jedes Eisenabschnitts erhält seinen zugehörigen Wert aus den CAD-Daten über die Compound-Parameter:
  
  • Der Anfangswert des magnetischen Flusses Phi0 wird in den Wirbelstrom-Elementen nicht fixiert. Sein Wert ergibt sich aus dem Anfangswert des Flusses des in Reihe liegenden Eisenwiderstandes.
  • Hinweis: Die Wirbelstrom-Elemente enthalten zusätzlich die zeitliche Ableitung des magnetischen Flusses Phidot als Zustandsgröße. Dessen Anfangswert wird durch Phidot0 festgelegt. Es ist es nicht erforderlich, Phidot0 zu fixieren (oder einen Wert zuzuweisen), da die automatische Initialisierung den korrekten Wert ergibt.
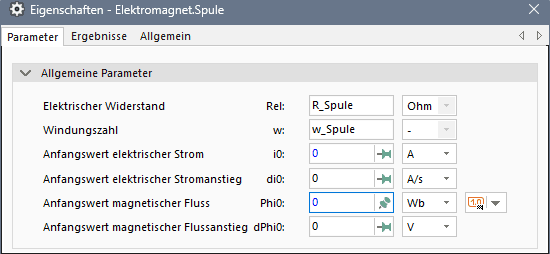
• Im Spulen-Element wird weiterhin nur der Anfangswert des magnetischen Flusses Phi0 für die Einspeisung in den Eisenabschnitt des inneren Magnetkreis-Eisenabschnittes wertmäßig festgelegt:

• Infolge der Reihenschaltung fließt der gleiche magnetische Fluss auch durch das Wirbelstrom-Element des inneren Eisenabschnittes.
• Danach verzweigt sich dieser Flusswert entsprechend der aktuellen magnetischen Widerstandswerte in zwei Äste: Spulenstreuung (also durch den Luftraum der Spule) und äußerer Eisenabschnitt.
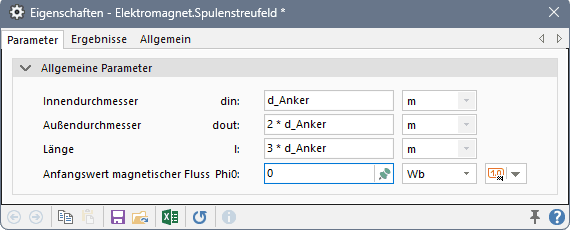
• Da im äußeren Eisenabschnitt keine Fixierung des Fluss-Anfangswertes erfolgt, muss zur Erzielung von Eindeutigkeit eine Fixierung des Flusses in der Spulenstreuung vorgenommen werden:

• Hinweis: Seit dem Einfügen der Wirbelstrom-Elemente entspricht diese Anfangswert-Fixierung einer nachvollziehbaren Logik! In der Etappe2a (ohne Wirbelstrom) führte diese Fixierung leider zu einer Überbestimmung des generierten Gleichungssystems (anscheinend durch "intelligente" Optimierungen bei der Modell-Analyse?).

Auf der Modell-Ebene müssen die Magnet-Parameter für die Wirbelstromwiderstände noch mit den zugehörigen Werten der CAD-Parameter gespeist werden:

• Wir setzen zur Validierung des Modells vorläufig den Gesamt-Wirbelstromwiderstand CAD.Re_Eisen auf einen großen Wert, z.B. 1 kΩ. Damit fließt praktisch kein Wirbelstrom und der Antrieb müsste sich so verhalten, wie wir es in den eingefrorenen Signalverläufen archiviert haben.
• Die Signalverläufe müssen mit diesen Einstellungen exakt deckungsgleich zur Simulation ohne Wirbelstrom-Elemente sein.

Problem:

• Leider werden bei jeglichen Änderungen innerhalb eines lokalen Compounds alle eingefrorenen Signalverläufe gelöscht!
• Man kann das Modell von Etappe2a mit seinen Ergebnissen zusätzlich im gleichen SimulationX-Programm öffnen, um die um die aktuellen Ergebnisse zu überprüfen.
• Ist man sicher, dass mit dem großen Wirbelstromwiderstand das gleiche Verhalten entsteht, wie ohne Wirbelstrom, kann man den aktuellen Verlauf als Vergleichsbasis wieder einfrieren.

Wirkung des Wirbelstroms

Nachdem unser Modell mit "unwirksamen" Wirbelstrom-Elementen funktioniert, wollen wir untersuchen, in welcher Größenordnung der Wirbelstromwiderstand praktisch liegen wird:

• Wir verringern den Wirbelstromwiderstand soweit, bis man "mit gesundem Menschenverstand" eine minimale Wirkung im Modellverhalten erkennt:

• Die Wirkung des implementierten Wirbelstromeffekts äußert sich hierbei in einer leichten Verzögerung des Abfallvorgangs. Der Stromsprung beim Einschalten liegt unter 1 mA und ist praktisch nicht erkennbar.

Hinweise::

• Wir merken uns die Größenordnung des Wirbelstromwiderstands, der zu einem merklichen Effekt führt.
• Für die folgenden Untersuchungen wird vorausgesetzt, dass in der Simulationsteuerung die Protokollschrittweite verringert wurde, damit wir die Wirbelstromeffekte im Spulenstrom erkennen können (z.B. dtProtMin=(tStop-tStart)/1000).

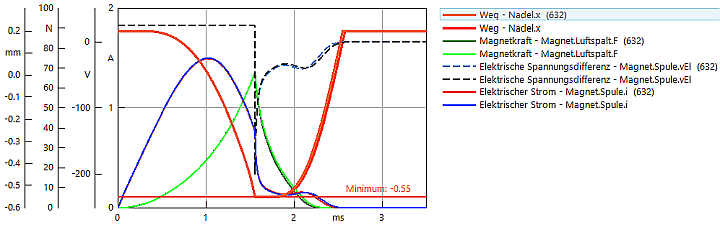
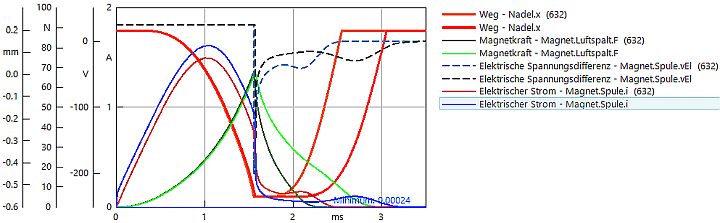
Als nächstes wollen wir den unteren Grenzwert für den Wirbelstromwiderstand abschätzen. Dazu verringern wir ihn soweit, bis der Stromsprung nach dem Einschalten ungefähr 10% vom maximal zulässigen Spulenstrom beträgt. Das sind 0.15 A bei einem zulässigen Strom von 1.5 A:

• Trotz der Änderung des Stromverlaufs beim Einschalten, ist die Auswirkung auf den Anzugsvorgang kaum erkennbar. Die Ursache liegt in der vereinfachten Modellierung des Wirbelstroms. Die Feldverdrängung innerhalb des Eisenquerschnitts wird damit nicht nachgebildet. Somit wirkt im Modell jetzt ein größerer effektiver Eisenquerschnitt als in der Realität.
• Nicht zu übersehen ist hingegen die Auswirkung auf den Abschaltvorgang. Der Kraftabbau verläuft verzögert und es dauert relativ lange, bevor die Rückholfeder den Anker zurückbewegen kann. Die optimale Dimensionierung des Antriebs wird unter Berücksichtigung dieses Wirbelstromeffekts zu veränderten Parametern führen.
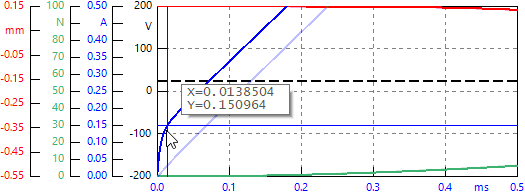
• Im Zoom erkennt man deutlich, dass der Stromsprung "abgerundet" ist, wie wir es auf Grund der Modellstruktur erwartet haben:

Im nächsten Schritt werden wir unter Berücksichtigung des ermittelten Wirbelstroms eine erneute Nennwert-Optimierung vornehmen.

← →