Software: SimX - Magnetoptimierung - Magnetische Durchflutung anstatt konkreter Spule
Mit dem bisherigen Finite Element Modell gewinnt man Kennfelder des Wandlers, welche nur für eine konkrete Anzahl von Windungen gültig sind:
- Ein wesentlicher Aspekt der Magnetoptimierung ist die Ermittlung einer optimalen Windungszahl.
- Variationen der Windungszahl im Optimierungsprozess würden deshalb ständig Aktualisierungen der Kennfelder mittels langwieriger FEM-Simulationen erfordern.
Um die Windungszahl als Parameter des Finite Element Modells zu elimieren, nehmen wir folgende Änderungen vor:
- Ersatz des Spulenstroms i durch die magnetische Durchflutung i*w
- Ersatz des Koppelflusses Psi durch den magnetischen Flus Fluss Psi/w
Magnetische Durchflutung
In der Öffnung unserer relativ langen Zylinderspule gilt bei hunderten Windungen näherungsweise für die magnetische Durchflutung
Ohne das bisherige Modell zu zerstören, werden wir die Möglichkeit ergänzen, die Durchflutung iw als unabhängige Variable zu benutzen:
- Ist iw< 0, so soll das Modell wie bisher über iSpule und wSpule parametrisiert werden.
- Ist iw>=0, so wird iSpule=iw/wSpule benutzt. Es wird eine hinreichend große Windungszahl benutzt(z.B. wSpule=1000).
Dazu wird Magnet.LUA wie folgt erweitert:
:
iw=-1; -- mag. Durchflutung (deaktiviert)
-- Parameter aus Textdatei einlesen mit Fehlertest
in = openfile(mydir .. "Eingabe.txt","r"); -- Datei öffnen zum Lesen
if in then -- wenn Datei geöffnet, dann Werte einlesen
read(in, "*l"); dMagnet= read(in, "*l", "*n");
read(in, "*l"); hTopf = read(in, "*l", "*n");
read(in, "*l"); dAnker = read(in, "*l", "*n");
read(in, "*l"); lAnker = read(in, "*l", "*n");
read(in, "*l"); hDeckel= read(in, "*l", "*n");
read(in, "*l"); dStift = read(in, "*l", "*n");
read(in, "*l"); dWand = read(in, "*l", "*n");
read(in, "*l"); wSpule = read(in, "*l", "*n");
read(in, "*l"); dLack = read(in, "*l", "*n");
read(in, "*l"); sWickel= read(in, "*l", "*n");
read(in, "*l"); sAnker = read(in, "*l", "*n");
read(in, "*l"); sDeckel= read(in, "*l", "*n");
read(in, "*l"); sGleit = read(in, "*l", "*n");
read(in, "*l"); iSpule = read(in, "*l", "*n");
read(in, "*l"); iw = read(in, "*l", "*n"); if iw == nil then iw=-1; end;
else print("Could not open Eingabe.txt"); end;
closefile(in);
-------------------------------------------------------------------------------
-- Unzulässige Eingabe-Parameter begrenzen / Umschaltung zwischen i und i*w --
-------------------------------------------------------------------------------
if 1*sAnker < 0.03 then sAnker=0.03; end;
if 1*sAnker > 5 then sAnker=5; end;
if 1*sGleit < 0.05 then sGleit=0.05; end;
if 1*sGleit > 1 then sGleit=1; end;
if 1*sDeckel < 0.01 then sDeckel=0.01; end;
if 1*sDeckel > 1 then sDeckel=1; end;
-- Wenn iw negativ, wird die Durchflutung aus iSpule*wSpule berechnet --
if 1*iw < 0 then iw=iSpule*wSpule; else wSpule=1000; end;
iSpule = iw/wSpule;
if 1*iSpule <=1E-3 then iSpule=1E-3; end; -- damit R und L berechenbar!
:
Die Kennfeld-Identifikation in OptiY muss mit diesem LUA-Script dass gleiche Ergebnis erzielen, wie zuvor.
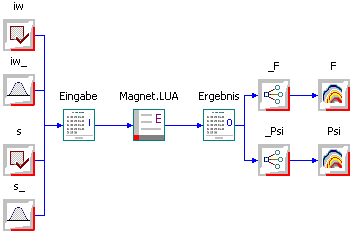
Wir werden nun den Experiment-Workflow so umgestalten, dass anstatt des Spulenstroms die magnetische Durchflutung als Variable benutzt wird:
- Dazu erweitern wir zuerst das Input-File Eingabe.txt um den Wert für die Durchflutung, die wir mit einem negativen Wert vorläufig deaktivieren:
dMagnet 40 hTopf 27.5 dAnker 10 lAnker 10 hDeckel 2.5 dStift 1 dWand 1 wSpule 400 dLack 0.06 sWickel 0.5 sAnker 1.000000E+000 sDeckel 0.01 sGleit 0.1 iSpule 4.000000E+000 iw -1
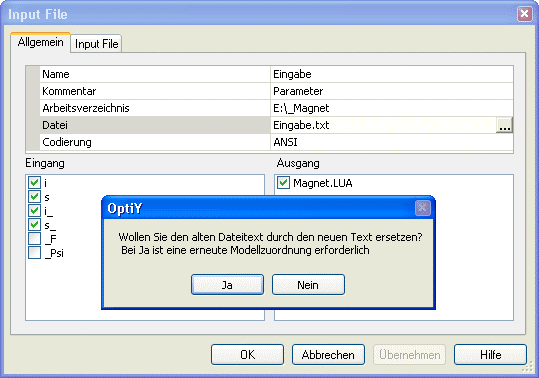
- Achtung: Das neue Input-File wird erst im Workflow benutzt, wenn man die Datei Eingabe.txt erneut öffnet:
- Die Zuordnung der Input-Variablen dürfte sich im Beispiel nicht ändern, da wir den neuen Parameter iw hinten angefügt haben. damit wurden die anderen Parameter-Positionen nicht geändert.
- Da die Variable iw infolge ihres negativen Wertes noch deaktiviert ist, ändert sich noch nichts an den Experiment-Ergebnissen.
- Wir nehmen nun die durchflutung "in Betrieb", idem wir im Workflow Nennwert und Streuung des Spulenstroms umdefinieren in die magnetische Durchflutung:
- Für die Kennfeld-Identifikation soll ein Durchflutungsbereich von iw= 0...4000 A erfasst werden. Das entspricht bei 1000 Windungen einem Spulenstrom von maximal 4 A.
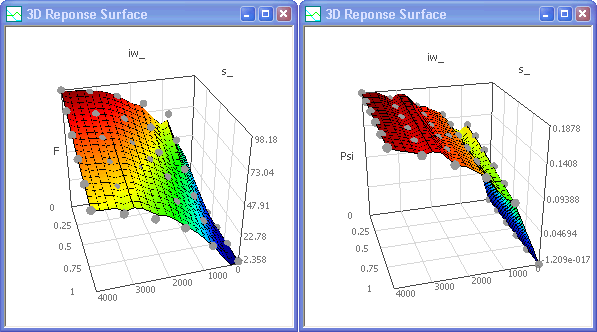
- Aufgrund des geänderten Scan-Bereiches kann die Qualität der identifizierten Kennfelder sich im Vergleich zu den vorherigen Ergebnissen verschlechtern:
- Im Beispiel verbesserte sich die Qualität auch ohne Anwendung des adaptiven Gaussprozesses durch Anwendung von Gamma-Exponential mit Polynomordnung=4 für beide Ergebnisgrößen:
- Achtung: Man muss sich bei den Ergebnissen jedoch bewusst sein, dass Psi der Koppelfluss für eine Windungszahl=1000 ist. Diesem Problem widmen wir uns als nächstes.
Magnetischer Fluss
Es ist kein Problem, aus dem vom FEMM ermittelten Koppelfluss Psi den magnetischen Fluss Phi durch die Spule im LUA-Script zu berechnen:
iSpule, vOhm, Psi = mo_getcircuitproperties("Spule"); -- statische Größen
print ("F=" , Fz_Anker, "[N]") -- Kraft in Outputfeld der LUA-Cosole
print ("iw=" , iw , "[A]"); -- Durchflutung
print ("i=" , iSpule , "[A]"); -- Strom
print ("w=" , wSpule , "[-]"); -- Windungszahl
print ("v=" , vOhm , "[V]"); -- Spannungsabfall
print ("R=" ,vOhm/iSpule,"[Ohm]");-- Drahtwiderstand
print ("L=" ,Psi/iSpule, "[H]"); -- Induktivität
print ("Psi=", Psi , "[Wb]"); -- Koppelfluss
Phi = Psi/wSpule;
print ("Phi=", Phi , "[Wb]"); -- magnetischer Fluss
-------------------------------------------------------------------------------
-- Output-File mit Ergebniswerten erzeugen
-------------------------------------------------------------------------------
out = openfile(mydir .. "Ergebnis.txt", "w");
write (out,"F=" , Fz_Anker, "\n");
write (out,"Psi=" , Psi , "\n");
write (out,"Phi=" , Phi , "\n");
closefile(out);
-- exit();
Der berechnete Wert von Phi wird in das Output-File geschrieben und kann von dort in den OptiY-Workflow übernommen werden:
- Damit die Datei Ergebnis.txt aktualisiert wird, muss man Magnet.LUA im FEMM abarbeiten!
- In Analogie zu iw definieren wir im Experiment-Workflow die Ausgangs- und Bewertungsgröße des Koppelflusses Psi in den magnetischen Fluss Phi um.
- Die Ausgangsgröße _Phi verknüpfen wir mit dem Wert von Phi in dem Output-File Ergebnis.txt.
Hinweis:
- Mit höherer Polynomordnung oder einer komplexeren Ersatzfunktion kann man nachträglich durch manuelles "Probieren" noch eine verbesserte Kennfeld-Qualität erreichen.
- Für die Durchführung eines adaptiven Design mittels Gauss-Prozess sollte man jedoch eine stabile Konfiguration wählen.
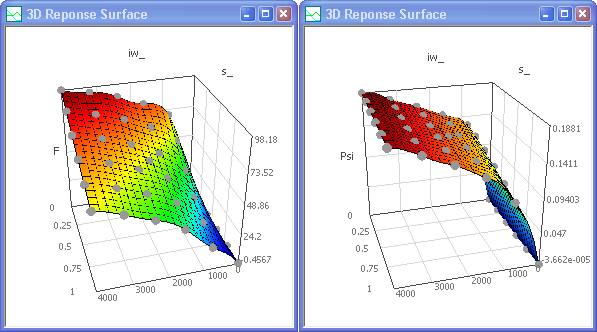
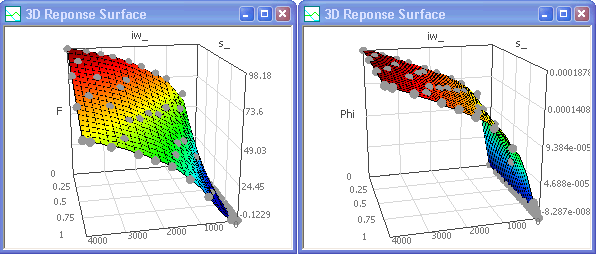
Deshalb führen wir das Full Factorial adaptive Design (4 Stufen) mittels Gauss-Prozess wieder mit folgender Konfiguration für die Antwortflächen durch:
F ... Exponential mit Polynomordnung=2 Phi ... Gamma Exponential mit Polynomordnung=2
Die Glattheit des Phi-Kennfeldes wurde durch nachträgliche Erhöhung der Polynomordnung auf 4 erreicht: