Software: SimX - Einfuehrung - Elektro-Chaos - Oszillator

↑

← →

Sinus-Oszillator (Schaltungssimulation)

(Bei Zeitverzug überspringen!)

Um einem LC-Schwingkreis eine dauerhafte Sinusschwingung zu entlocken, muss man ihm mittels einer elektronischen Schaltung zu jedem Zeitpunkt exakt die Energie zuführen, welche durch die Verluste im Schwingkreis in Wärme umgewandelt wird (Siehe: Oszillator).

Eine mögliche Schaltung verwendet einen Differenzverstärker mit zwei Transistoren und zeichnet sich durch sehr gutmütiges Verhalten aus. Für die Schaltungssimulation benutzt man im Normalfall Spezialprogramme, z.B. die weit verbreitete SPICE-Software.

In Simulatoren zur System-Simulation, zu denen SimulationX gehört, kann man einfache elektronische Schaltungen ebenfalls problemlos simulieren. Man hat dann zwar den Nachteil fehlender Bauelement-Datenbanken. Jedoch kann man die Schaltungsmodelle direkt mit anderen physikalischen Domänen koppeln (z.B. mit elektro-mechanischen Aktuatoren).

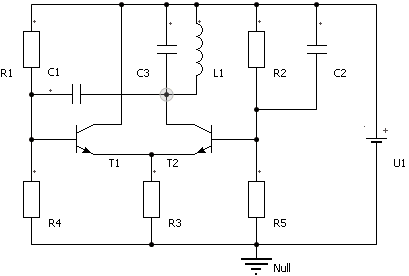
Wir bauen die Schaltung eines Sinus-Oszillators als neues SimulationX-Modell auf (Oszillator.ism):

Die Frequenz wird durch den Parallel-Schwingkreis aus L1 und C3 bestimmt:

• Wir verwenden eine Luftspule mit einer Induktivität L1=0.01 H.
• Es soll eine Frequenz von f₀=1 kHz erzeugt werden. Dafür ist die Kapaziät C3=? F zu ermitteln (verlustarmer Klasse-1-Keramik-Kondensator):

[math]\displaystyle{ f_0 = \frac{1}{2 \pi \sqrt{L C}} }[/math]

Für die restlichen Bauelemente verwenden wir folgende Parameter:

• Die Kapazitätswerte der anderen Kondensatoren sollen den gleichen Wert erhalten:
  C1=C2=C3.
• Alle Kondensatoren müssen am Anfang entladen sein: v0=0 (mit gesetzter "Reißzwecke"!).
• Die Widerstände besitzen folgende Werte:
  R1=R2=330 kΩ
  R4=R5=100 kΩ
  R3=4.7 kΩ
• Die Transistoren behalten ihre Vorgabewerte.
• Die Betriebsspannung beträgt U1=12V.

Die generierte Sinus-Spannung greifen wir am Kollektor von T2 z.B. mittels eines zusätzlichen Spannungssensors ab (Potentialpunkt in obiger Schaltung markiert). Diese Ausgangsspannung kann im Bereich von 0..24 V schwingen und soll in einem Signalfenster dargestellt werden..

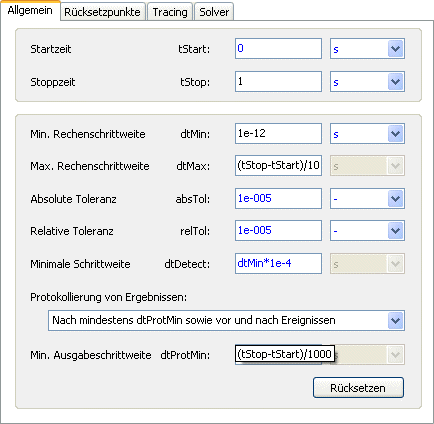
Wir konfigurieren die Simulation für einen Zeitbereich von tStop=1 s und mit einer hinreichend kleinen Protokollschrittweite dtProtMin:

• Nach dem Start der Simulation werden wir mit großer Wahrscheinlichkeit sofort mit einer Fehlermeldung überrascht:

• Solche Probleme haben wir für eine "harmlose" Sinusschwingung nicht erwartet!
• Die Sinusschwingung ergibt sich jedoch erst aus der Wechselwirkung insbesondere der beiden Transistoren, welche sehr kleine Zeitkonstanten besitzen. Damit wird insbesondere der Einschwingvorgang unmittelbar nach dem Einschalten sehr kritisch.
• Dieses Problem kann man mit Erfahrungswissen durch Verringern der minimalen Zeitschrittweite lösen, z.B. dtMin=1E-12 s:

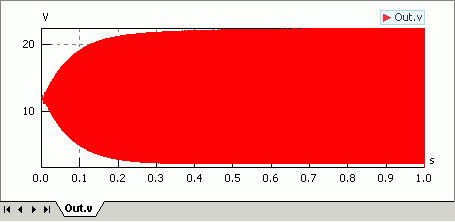
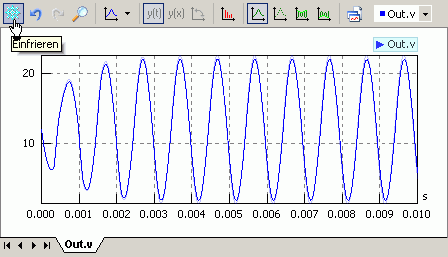
Danach sollte die Simulation ordentlich starten und plausible Ergebnisse berechnen:

Signalverarbeitung

Spätestens jetzt sollte man überprüfen, ob die mit dem analytisch dimensionierten Schwingkreis erzeugte Frequenz den richtigen Wert besitzt:

• Hier könnte man im Signalfenster die Dauer einer Schwingungsperiode ausmessen. Das ist etwas umständlich und fehleranfällig.
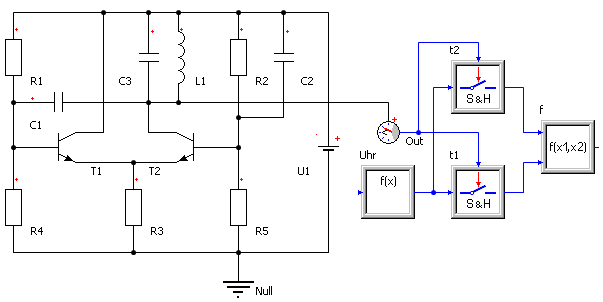
• Mit unseren Erfahrungen zur Signalverarbeitung werden wir uns eine Auswerte-Elektronik modellieren, welche die aktuelle Frequenz automatisch ermittelt:

• Die Uhr zum Messen der aktuellen Simulationszeit t wird durch ein Signalglied Function nachgebildet. Als Parameter F des Function-Blockes verwenden wir die globale Variable t, welche den aktuellen Wert der Simulationszeit enthält.
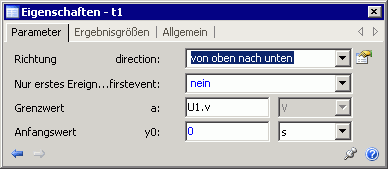
• Das Ausgangssignal der Uhr speisen wir in 2 ereignisgesteuerte Abtastglieder. Diese sollen die Zeitpunkte der Nulldurchgänge der Sinusspannung erfassen:
  
  • Die "Null-Linie" der Sinusspannung entspricht dem Wert der Betriebsspannung. Deshalb wird U1.V als Grenzwert für die Auslösung des Sample-Vorgangs definiert.
  • t1 und t2 erfassen jeweils die Zeitpunkte entgegengesetzter "Nulldurchgänge" der Sinusspannung. Somit sind die Ausgangs-Zeitwerte beider Abtastglieder immer um die Dauer der letzten Halbwelle versetzt.
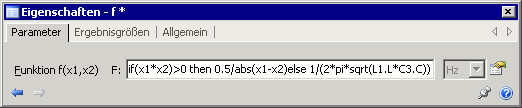
• Ein Signalblock Function2 erfasst mit seinen beiden Eingängen x1 und x2 die beiden gesampelten Zeitwerte und berechnet daraus die aktuelle Frequenz F: 0.5/abs(x1-x2)
  • Leider stürzt die Simulation damit sofort nach dem Start mit "Division durch Null" ab, weil für t1.y und t2.y jeweils nur der Anfangswert y0=0 vorliegt.
  • Deshalb ist bei der Frequenzberechnung dieser Fall separat zu behandeln. Es genügt dafür die Bedingung x1*x2>0.
  • Für die Zeit der ersten Periode wollen wir aus den Schwingkreis-Parametern analytisch den Wert der Resonanzfrequenz berechnen:

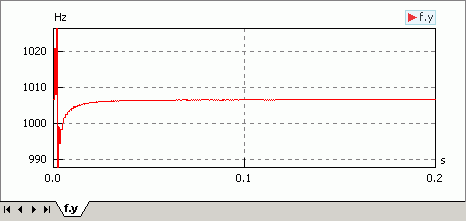
• Der eingeschwungene Zustand wird im Beispiel nach ca. 0.2 s erreicht. Für diesen Zeitbereich betrachten wir nun den Frequenzverlauf des Oszillators:

• Bereits nach wenigen Perioden ist die endgültige Frequenz erreicht. Die erzeugte Frequenz liegt im Beispiel wenige Hertz oberhalb von 1 kHz. Ursache ist die Rundung des Kapazitätswertes für C3 auf 2 Ziffernstellen.

Frage 6: Welcher "exakte" Kapazitätswert (gerundet auf 4 Ziffernstellen) müsste bei dem vorgegebenem "exakten" Induktivitätswert L1=0.01 H für eine Frequenz von 1 kHz verwendet werden?

Verlustbehafteter Parallel-Schwingkreis

Bisher funktioniert unsere Oszillator-Schaltung recht gut. Dabei kann man schnell vergessen, dass hier nicht die Schaltung selbst funktioniert, sondern ein Modell der Schaltung! Das Verhalten kann in der Realität ganz anders aussehen, weil wir einen wichtigen Effekt im Modell vergessen haben:

• Eine Spule besitzt immer einen ohmschen Widerstand infolge des Spulendrahtes, wenn man nicht den Spezialfall der Supraleitung betrachtet. Das führt zu den bereits untersuchten gedämpften Schwingungen des passiven LC-Schwingkreises.
• Auch der Kondensator arbeitet nicht verlustfrei. In unserem Beispiel können wir aber seine Verluste im Vergleich zu den Spulenverlusten vernachlässigen.
• Wir ergänzen in unserem Modell in Reihe zur Induktivät einen Widerstand R_Spule, für den wir wieder einen Wert von 1.3 Ω annehmen.
• Hinweis: In der Student Edition von SimulationX kann man nur 5 Widerstandselemente verwenden. Wir benutzen deshalb ein Leitwert-Element mit G=1/R als Serienwiderstand zur Induktivität.

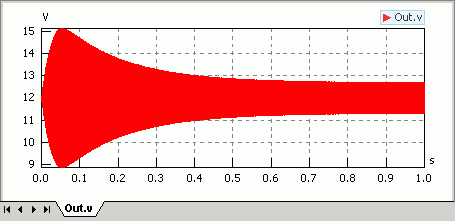
Nach dem Ergänzen des Spulenwiderstands ändert sich das simulierte Verhalten beträchtlich:

• Die Schwingungsamplitude beträgt ca. nur noch 1/10 im Vergleich zum idealen, verlustfreien Schwingkreis.
• Die Frequenz bleibt jedoch praktisch gleich.

Diese starke Abhängigkeit vom konkreten Spulenwiderstand zeigt, dass die Schaltung noch nicht optimal dimensioniert wurde. Mit Hilfe von Simulationsexperimenten werden wir die Schaltung so dimensionieren, dass wir bis zu einem Spulenwiderstand von 2 Ω eine Signal-Amplitude von mindestens 10 V (bezogen auf den Mittenwert von 12 V) erzeugen können:

• Sicher kann man eine exakte analytische Dimensionierung dieser Schaltung in der Literatur finden. Bei genügend Expertenwissen, kann man die erforderlichen Gleichungen auch selbst herleiten.
• Wir wählen hier jedoch den pragmatischen Weg der "wohlüberlegten" Modifikation.
• Die Widerstände der Schaltung sind ziemlich hochohmig. Dadurch ist die Schaltung nicht in der Lage, die Verluste in der Spule im erforderlichen Maße zu kompensieren.
• Das kann man sehr schnell überprüfen, indem man z.B. alle Widerstände (außer R_Spule) auf ein Zehntel ihres bisherigen Wertes reduziert. Der Erfolg für den bisherigen Wert R_Spule=1.3 Ω ist offensichtlich:

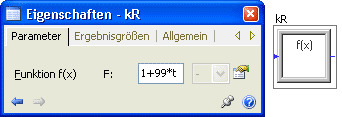
Es ist umständlich, durch iterative Variation aller Widerstände eine optimale Widerstandskonfiguration zu finden. Deshalb werden wir diese Experimente etwas rationalisieren, indem wir mittels eines Funktionsblockes f(x) im Modell einen globalen Faktor kR definieren. Mit diesem Faktor verändern wir dann alle Widerstände der Schaltung gleichzeitig:

• Die Funktion F wurde so gewählt, dass im Zeitbereich bis tStop=1 s sich der Reduktionsfaktor von 1 auf 100 erhöht.
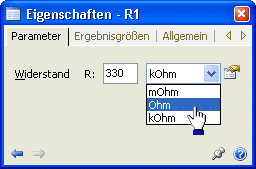
• Wir setzen alle Widerstandswerte auf ihren ursprünglichen Wert zurück. Als Maßeinheit wählen wir Ohm, weil nach dem späteren Ergänzen einer Gleichung mit dem Faktor kR der Wert physikalischer Größen in der SI-Einheit berechnet wird:

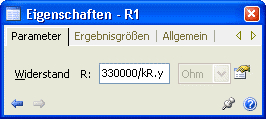
• Danach ergänzen wir für die in Ohm angegebenen Widerstandswerte den Reduktionsfaktor:

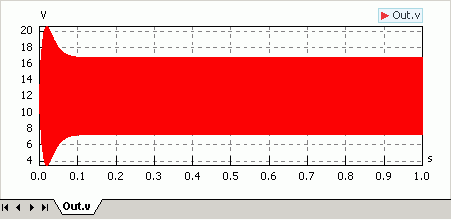
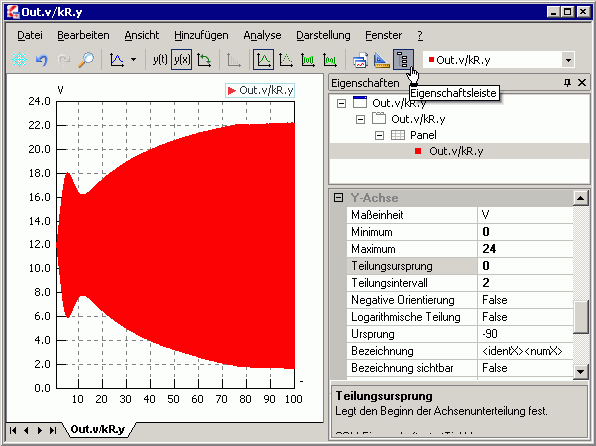
• Während der Simulation werden die Widerstandswerte kontinuierlich verringert und damit erhöht sich stetig die Amplitude der Signalspannung bis zu ihrem Maximalwert.
• Bei sinnvoller Beschriftung der Y-Achse des Signalfensters braucht man sich jetzt nur noch für den kleinst möglichen Reduktionsfaktor kR entscheiden (Konfiguration über Eigenschaftsleiste - für Y-Achse Autoskalierung deaktivieren und manuell konfigurieren):

• Im Beispiel konnte mit R_Spule=2 Ω ein fast identisches Schwingungsverhalten erzielt werden, wie mit einer idealen verlustfreien Spule (blasse, eingefrorene Kurve mit etwas höherer Amplitude). Der eingeschwungene Zustand wird mit dieser optimierten Dimensionierung nun wesentlich schneller erreicht:

Frage 7: Welche effektive thermische Verlustleistung wird in der optimierten Schaltung am Widerstand R3 erzeugt?
Hinweise: Die Verlustleistung P=u*i wird in jedem Widerstandselement als Ergebnisgröße Pl berechnet. Zeigt man diese berechnete Leistung in einem Signalfenster an, kann man als Hilfslinie den "Effektivwert" einblenden (Hinzufügen > Horizontale Linie > Effektivwert).

← →