Software: SimX - Einfuehrung - Elektro-Chaos - Luftspule
Eine elektrische Induktivität wird meist durch einen stromdurchflossenen Leiter realisiert. Infolge des Stromflusses wird ein magnetisches Feld um den Leiter aufgebaut. Eine Induktivität speichert die eingespeiste elektrische Energie in Form der Energie des resultierenden magnetischen Feldes.
Da der Mensch magnetische Felder nicht direkt wahrnehmen kann, sind sie "unanschaulicher" als elektrische Felder, deren Wirkung bestimmt schon jeder in irgendeiner Form gespürt hat.
Magnetfelder sind uns neben beobachtbarer Kraftwirkungen vor allem über ihre Wechselwirkung mit den elektrischen Feldern zugänglich. Eine Effekt der Induktivität ist z. B. die Selbstinduktionsspannung entlang des Leiters, wenn sich der durchfließende Strom ändert. Daraus leitet sich auch die Einheit Henry (H) ab (1 H = 1 V·s/A). Eine Spule besitzt eine Induktivität von 1 H, wenn sich bei einer konstanten Stromänderung von 1 A/s ein Spannungsabfall von 1 V an den Spulenanschlüssen ergibt.
Der Wert der Induktivität einer Spule ist abhängig von der Permeabilität des Materials, in welchem sich das Magnetfeld aufbaut. Einen wesentlichen Einfluss auf die Vergrößerung der resultierenden Induktivität haben dabei nur ferromagnetische Stoffe. Da die Permeabilität dieser Stoffe von der Stärke des Magnetfeldes abhängt und zusätzlich eine Hysterese aufweist, führt dies jedoch zu nichtlinearen Induktivitäten. Deren Induktivitätswert ist abhängig vob der Stärke des fließenden Stromes und der Vorgeschichte.
Wir beschränken uns in dieser Übung auf lineare Induktivitäten, deren Wert sich nicht in Abhängigkeit von den Einsatzbedingungen ändert. Das ist bei Luftspulen gegeben, weil sich die Permeabilität von Luft unabhäng von Feldstärken, Temperatur, Feuchtigkeit und Luftdruck praktisch nicht ändert (im Bereich von 1e-5).
Einschalt-Experiment
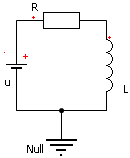
Analog zum Auflade-Experiment mit dem RC-Glied untersuchen wir den Anstieg des Spulenstroms nach Anlegen einer Spannung an ein RL-Glied. Dazu schließen wir unsere Modelldatei RC-Glied.ism und beginnen die Arbeit an einer neuen Datei RL-Glied.ism.
Um die Symbole beim Aufbau der Modellschaltung zu drehen, aktivieren wir zuvor die Element-Symbolleiste.
Die Zeitkonstante des RL-Glieds ist der Quotient aus der Induktivität und dem Widerstand:
- [math]\displaystyle{ \tau=\frac{L}{R} }[/math]
Der Anstieg des Stromes erfolgt dabei analog zur Aufladespannung am Kondensator mit:
- [math]\displaystyle{ i(t) = \frac{U}{R} \cdot (1 - e^{-\frac{t}{\tau}}) \, }[/math]
τ gibt die Zeit an, nach welcher der Strom durch die Induktivität ca. 63,2 % des Endstromes erreicht hat. Nach 5 · τ hat der Strom etwa 99,3 % seines Endwertes erreicht, was praktisch dem Endstrom entspricht. Der Strom wird durch das ohmsche Gesetz auf i=U/R begrenzt.
Mit Luftspulen ist es praktisch nicht möglich, eine Zeitkonstante von 1 s zu erreichen:
- Die Induktivität steigt zwar quadratisch mit der Windungszahl. Trotz tausender Windungen sind Luftspulen mit 1 H technisch wegen ihrer Größe kaum realisierbar.
- Der für die Spulenwindungen benötigte Draht besitzt einen ohmschen Widerstand, der als Bestandteil des Reihenwiderstand R zu betrachten ist. Es ist ohne die Nutzung von Supraleitung nicht möglich, Luftspulen hoher Induktivität mit einem Spulenwiderstand von wesentlich kleiner als 1 Ω zu realisieren.
Analog zum Auf- und Entlade-Experiment eines Kondensators führen wir selbständig die Experimente zum Ein- und Ausschalten einer Induktivität durch. Die interessierende dynamische Zustandsgröße ist jetzt die Spulenstrom. Wir gehen in folgenden Schritten vor:
- Aufbau des Schaltungsmodells lt. obiger Skizze.
- Dimensionierung des Widerstands R für eine Zeitkonstante von τ = 1 ms bei einer Induktivität L =1 mH.
- Konfiguration der Simulation für eine Zeitbereich von 5 ms.
- Überprüfung der markanten Zeitpunkte auf richtige Stromänderung durch Ausmessen der Signale.
- Erweiterung des Modells um einen Stromsensor.
- Automatische Erfassung des Zeitpunktes für das Erreichen eines vorgegebenen Stromwertes.
Frage 2:
- Zu welchem Zeitpunkt t wird für das Beispiel exakt ein Stromwert von 90% des Maximalwertes beim Einschalten erreicht?
