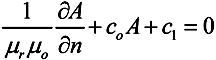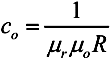Software: FEM - Tutorial - Magnetfeld - Randbedingungen
Überblick
- Über Zwangsbedingungen kann man definieren, wie sich das Feld über den Rand des Modells hinaus ausbreiten soll. Die richtigen Randbedingungen sind entscheidend für die Modell-Genauigkeit.
- Das ist abhängig von der Art des Materials, welches an den Modellrand grenzt und der Form des Modellrandes. Die Formulierung der Randbedingungen ist oft kein triviales Problem!
- Im Beispiel des magnetischen Wirbelfeldes muss man den unendlichen Luftraum nachbilden, in den sich das Streufeld des Magneten erstreckt ("Open Boundary Problem").
Für das elektrostatische Problem der Leiter-Kapazität hatten wir solch ein "Open Boundary Problem" bereits definiert. An dieser Stelle sollen die verschiedenen Ansätze für diese Art von Randbedingungen insbesondere unter dem Aspekt des Magnetfeldes näher betrachtet werden. Für "Open Boundary Problems" kann man drei grundsätzliche Ansätze unterscheiden, welche nach Mathematikern benannt sind:
- Dirichlet (Mathematiker 1805-1859)
Wird die abhängige Variable auf dem Rand direkt vorgegeben, liegt eine "Dirichlet Randbedingung" vor. Im Wirbelfeld erhält das Vektorpotential am Rand des Modells einen festen Wert. Für magnetische Probleme wird dabei das Vektorpotential entlang der Grenzlinie meist A=0 gesetzt. Damit verhindert man den magnetischen Fluss über diese Grenzlinie hinweg.
Diese Art der Randbedingung setzt voraus, dass um den betrachteten Magnetkreis sich möglichst wenig Streufeld in den Luftraum erstreckt. Bei dem betrachteten Topfmagneten wäre dies der Fall. Wenn man hier einen hinreichend großen Luftraum modelliert (ca. 5x so groß wie der Magnet selbst), so könnte man den äußeren Rand dieses Bereiches mit dem Vektorpotential A=0 belegen.
Hinweis: Für axialsymmetrische Probleme wird die Symmetrieachse (r=0) automatisch mit A=0 belegt. - Neumann (Mathematiker 1832-1925)
Wird nicht der Wert selbst, sondern seine örtliche Ableitung senkrecht zur Grenzlinie vorgegeben, liegt eine "Neumann Randbedingung" vor. Für magnetische Probleme (mit n=Normalenvektor zur Grenze) setzt man δA/δn = 0.
Diese Randbedingung zwingt den magnetischen Fluss, exakt im Winkel von 90° die Grenze zu durchdringen. Dies beschreibt einen Übergang zwischen einem Material geringer Permeabilität im Modell (z.B. µo für Luft) und einem Material hoher Permeabilität außerhalb des Modells (z.B. Eisen).
Hinweise:- Wird im FEMM-Modell keine Randbedingung definiert, so wird standardmäßig die "Neumann Randbedingung" verwendet. Das widerspiegelt aber selten die Realität (Luft um den Magneten)!
- Zusätzlich zur "Neumann Randbedingung" muss mindestens eine ableitungsfreie Randbedingung existieren, um eine eindeutige Lösung zu erhalten! Für axialsymmetrische Magnetprobleme ist dies durch die Belegung der Symmetrieachse gesichert. Ansonsten muss für mindestens einen Punkt (Knoten des Netzes) der Wert des Vektorpotentials vorgegeben werden.
- Robin (Mathematiker 1855-1897)
Bei der "Robin Randbedingung" handelt es sich um einen Mix aus obigen beiden Formen. Beschrieben wird eine Abhängigkeit zwischen dem Wert von A und seiner "Normalen-Ableitung" an der Grenze. Ein Beispiel für solch eine Randbedingung ist δA/δn+c·A = 0.
Durch diese Randbedingung ist es möglich, mit einem begrenzten Modellbereich das Verhalten einer unbegrenzten (unendlich großen) Region nachzubilden.
Hinweis: Auch hier ist zusätzlich eine ableitungsfreie Randbedingung für eine eindeutige Lösung erforderlich!
Modellierung
In unserem Beispiel soll der unendliche Luftraum durch eine Kugelgrenzfläche mit dem Radius R=rKugel [mm] nachgebildet werden. Dafür ist eine geeignete Robin-Randbedingung zu definieren. Die "asymptotische Randbedingung" beschreibt den Verlauf der Feldlinien an der betrachteten Grenze. Die folgende Gleichung setzt voraus, dass auf beiden Seiten der Grenze die gleiche relative Permeabilität existiert und die Grenze selbst eine Kugelfläche darstellt:
mit 
und 
Da unsere Grenze in Luft verläuft, ist µr=1. Der Radius R ist in Meter anzugeben, unabhängig von der gewählten Maßeinheit des Problems! A ist das magnetische Vektorpotential und n repräsentiert den Normalenvektor zur Grenzfläche, in unserem Beispiel der Kugeloberfläche.
Hinweis: Der Zählerwert=1 im Bruch für die Berechnung von c0 ist der problemabhängige Wert für n und gilt nur für den speziellen Fall des magnetischen Dipols im achsensymmetrischen Problem! Falls man z.B. statt einer Dipolspule mehrpolige Permanentmagnet-Anordnungen berechnen möchte, muss man für n einen anderen Wert einsetzen.
Robin-Randbedingung (Mixed-Type):
-------------------------------------------------------------------------------
-- Randbedingungen für die Kugelsphäre als "Open Boundary Conditions" --
-------------------------------------------------------------------------------
-- mi_addboundprop("name", A0, A1, A2, Phi, Mu, Sig, c0, c1, BdryFormat);
-- BC-Type Mixed: DdryFormat=2, c0 und c1 wie berechnet, alle anderen Parm=0
c0=1/(uo*rKugel*mm); c1=0;
mi_addboundprop("RobinBC", 0, 0, 0, 0, 0, 0, c0, c1, 2);
- c0 wird abhängig von der aktuellen Magnetgröße berechnet: 1/(uo*rKugel*mm).
- In der Lua Scriptsprache von FEMM ist uo=µ0 . Das trotz Angabe von rKugel in [mm] der Radius in Metern benutzt wird, ist Aufgabe des Faktors mm=0.001.
Den Erfolg der Definition sollte man wieder überprüfen:
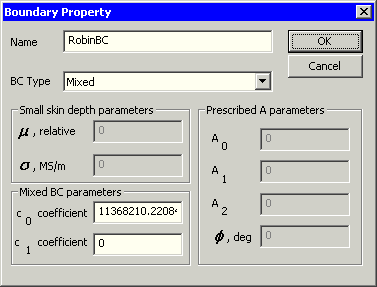
- Über Properties - Boundary - Modify Property erscheint der Parameter-Dialog für die Randbedingung:
- Diese Randbedingung muss nun der Kugeloberfläche zugewiesen werden:
mi_seteditmode ("arcsegments");
-- mi_selectarcsegment ( r ,z); -- Select the arc segment closest to (r,z)
mi_selectarcsegment (rKugel,0); --> Mittelpunkt des Bogens
-- mi_setarcsegmentprop(maxsegdeg,"propname",hide,group);
mi_setarcsegmentprop( 3 ,"RobinBC" , 0 , 0 );
mi_clearselected();
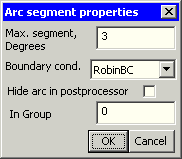
Den Erfolg der Zuweisung sollte man nach Abarbeitung des Lua-Scripts wieder über die grafische Oberfläche überprüfen:
- Im Kreissegment-Modus
und wählt man den Halbkreis durch Anklicken mit der rechten Maustaste. - Nach Betätigen der Leertaste oder
gelangt man in den Dialog, der die Zuordnung der Randbedingung anzeigt.
