Software: FEM - Tutorial - Magnetfeld - Potentialfeld-Analogie
In den bisherigen Übungen haben wir zur FEM-Simulation elektrischer Felder in Autodesk Fusion die Analogien zum Temperatur-Feld benutzt. Nur so konnte man mit den Mitteln dieses FEM-System die elektrische Domäne behandeln. Zur Erinnerung werden diese Analogien hier noch einmal dargestellt:
|Temperatur-Feld |Elektr. (Fluss-)Feld |Elektrostatisches Feld --------------------------------------------------------------------------------- Potential |Temperatur |elektrische Spannung |el.statisches Potential . |[K] |[V] |[V] --------------------------------------------------------------------------------- Pot.Gradient |Temperatur-Gradient |el. Spannungsabfall |Feldstärke . |[K/m] |[V/m] |[V/m] --------------------------------------------------------------------------------- Material- |Wärmeleitfähigkeit |spez. el. Leitfähigk. |Dielektrizitätskonst. eigenschaft |[W/(K·m)] |[1/(Ohm·m)] |[(A·s)/(V·m)] --------------------------------------------------------------------------------- Flussgröße |Wärmestrom |Elektrischer Strom |Verschiebung (Ladung) . |[W] |[A] |[A·s] --------------------------------------------------------------------------------- Flussdichte |Wärmestromdichte |Stromdichte |Ladungsdichte "Flächenlast"|[W/m²] |[A/m²] |[(A·s)/m²]
Auch für die magnetische Domäne kann man solche Analogien definieren, wobei sich je nach Zielstellung unterschiedliche Varianten von Analogiebeziehungen bewährt haben. Problematisch bei der Analogie zum Temperaturfeld ist der Wirbelfeld-Charakter des Magnetfeldes (Quellenfreiheit)!
{C} Wärmekapazitätsmatrix
{T'} Vektor der Temperaturänderungsgeschwindigkeit
{K} Leitfähigkeitsmatrix
{T} Temperaturvektor
{Q(t)} Wärmestromvektor
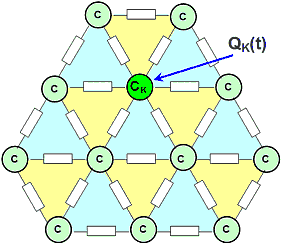
Die Wärmegleichung beschreibt die Leistungsbilanz für jeden Knoten:
- Q(t) Energiefluss zur Netzumgebung (Last)
- C·T' Energiefluss in Wärmespeicher des Knoten
- K·T Energiefluss über die Wärmeübergangswiderstände zu den Nachbarknoten
Analogien zum Magnetfeld lassen sich nur für den statischen Fall aufstellen, d.h., wenn Speicherelemente nicht berücksichtigt werden ({C}={0}). Dann gelten die bekannten Analogien:
{K} Permeabiltätsmatrix {µ}
{T} Vektor der magnetischen Potentiale {Vm}
{Q(t)} Vektor der magnetischen Flüsse {Φ}
Diese Analogien zwischen dem Temperatur- und dem Magnetfeld nun vollständig in tabellarischer Form:
|Temperatur-Feld |Magnetfeld ---------------------------------------------------------------- Potential |Temperatur |magnetische Spannung . |[K] |[A] ---------------------------------------------------------------- Pot.Gradient |Temperatur-Gradient |magnetische Feldstärke . |[K/m] |[A/m] ---------------------------------------------------------------- Material- |Wärmeleitfähigkeit |Permeabilität eigenschaft |[J/(K·m)] |[V·s/(A·m)] ---------------------------------------------------------------- Flussgröße |Wärmestrom |magnetischer Fluss . |[W] |[V·s=Wb] ---------------------------------------------------------------- Flussdichte |Wärmestromdichte |magn. Flussdichte (Induktion) "Flächenlast"|[W/m²] |[(V·s)/m²=T]
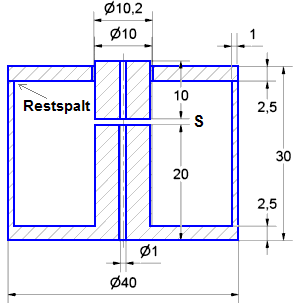
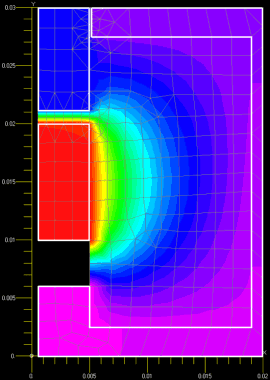
Damit diese Analogien funktionieren, muss man im räumlichen Bereich der MMK (=Spule) einen magnetischen "Isolator" (magn. Leitwert=0 H) vorsehen:
- Es genügt ein hinreichend großes "Loch" an der Spulen-Position im Netz.
- Wenn man an einer Seite des MMK-Loches eine Flussdichte in den magnetischen Kreis speist und die andere Seite mittels "Konvektion" auf Nullpotential zieht, stellt sich eine magn. Spannung über der MMK ein.
- Aus dem eingespeisten magnetischen Fluss und dem berechneten MMK-Wert kann man den magnetischen Widerstand des gesamten Magnetkreises (aus "Sicht" der MMK) berechnen.
Die Anwendung dieser Potentialfeld-Analogie für magnetische Kreise weist Schwächen auf:
- Magnetische Durchflutungen (Spulen) können nur eingeschränkt berücksichtigt werden, da es nicht möglich ist, den elektrischen Strom als Ursache des Magnetfeldes im Modell direkt zu berücksichtigen.
- Komplette Magnetkreise sind nur eingeschränkt modellierbar, da das Wirbelfeld "aufgeschnitten" und als Potentialfeld zwischen 2 magnetischen Polen betrachtet werden muss.
- Deshalb werden wir im Folgenden nur das FEMM-Programm benutzen, welches den Wirbelfeld-Charakter des Magnetfeldes behandeln kann!