Software: FEM - Tutorial - Magnetfeld - Physik

↑

← →

Physik des Magnetfeldes

Ein Stromdurchflossener Leiter ist immer mit einem Magnetfeld verknüpft. Die grundlegenden physikalischen Zusammenhänge werden im Folgenden kurz dargestellt.

Wirbelfeld

Die Feldlinien des magnetischen Feldes bilden geschlossene Linien um den stromdurchflossenen Leiter.

Magnetischer Kreis

Das ist der gesamte vom Magnetfeld erfüllte Raum um den stromdurchflossenen Leiter.

Magnetischer Fluss [Φ]=V·s (=Wb)

Das ist die gesamte in sich geschlossene Erscheinung, welche den Strom "umwirbelt" - die Richtung des Flusses ist mit der positiven Richtung des Stromes über eine "Rechtsschraube" verbunden.

In Wirklichkeit "strömt" bzw. "wirbelt" nichts, sondern es handelt sich nur um die Charakterisierung eines Raumzustandes!

Magn. Flussdichte (Induktion) [B=dΦ/dA_┴] = V·s/m² (=T)

Man spricht von "Quellenfreiheit", weil keine "magnetischen Ladungen" existieren und die Fluss(dichte)-Linien immer in sich geschlossen sind:

• ΣΦ_in=ΣΦ_out - der gesamte in ein Volumen-Element "hineinströmende" Fluss ist gleich der Menge des "herausströmenden" Flusses.
• _Hülle∫B·dA=0 - das Hüllenintegral der Induktion über die Oberfläche eines Volumen-Elements ist Null.

Magnetomotorische Kraft (Durchflutung) [Θ] = A

Die MMK ist gleich der Summe der umschlossenen Ströme, wenn man einen beliebigen geschlossenen Weg s im Magnetkreis betrachtet:

• Θ = Σi_x - die Ströme werden als "antreibende Kraft" für den Fluss entlang des betrachteten Weges im magnetischen Kreis interpretiert.
• _Umlauf∫B·ds=µ₀·Σi_x - das Umlaufintegral der Flussdichte entlang dieses Weges ist in Vakuum immer proportional zur Summe der umschlossenen Ströme (zur MMK).

Induktionskonstante µ_o = 4·π·10^-7 V·s/(A·m)

• _Umlauf∫B·ds=µ₀·Θ

µ₀ ist die Naturkonstante, welche das Umlaufintegral der Flussdichte längs eines Weges mit dem Wert der umschlossenen MMK verknüpft.

• c^-2 = µ₀·ε₀

Die enge Verknüpfung zwischen magnetischem und elektrischem Feld wird deutlich über den Zusammenhang zwischen Vakuum-Lichtgeschwindigkeit, Induktions- und Influenzkonstante.

Permeabilität

Legt man den Weg für das Umlaufintegral nicht durch Vakuum, sondern durch Ferromagnetika (Eisen, Nickel, Kobalt, Kupfermangan-Legierungen), so ist der Wert des Umlaufintegrals von B wesentlich größer als µ₀·Σi_x:

• d.h. bei gleichem el. Strom sind der magn. Fluss bzw. die Flussdichte wesentlich größer als in Vakuum (oder in nicht ferromagnetischen Stoffen).
• relative Permeabilität: dimensionsloser Faktor µ_r, welcher die magnetische Eigenschaft des jeweiligen Stoffes im Vergleich zum Vakuum charakterisiert.
• absolute Permeabilität: µ = µ_r·µ₀ mit der Einheit V·s/(A·m)

Magn. Feldstärke [H=B/µ] = A/m

• _Umlauf∫H·ds=Σi_x=Θ - Die Einführung der magnetischen Feldstärke hat den Vorteil, dass mit dieser Größe das Umlaufintegral entlang eines Weges unabhängig von den Stoffeigenschaften immer gleich dem Wert der umschlossenen Ströme ist (MMK=Durchflutung).
• Dieses "Durchflutungsgesetz" ist ein Grundgesetz des Magnetfeldes. Indem der elektrische Strom verallgemeinert als Summe von Konvektions- und Verschiebungsstrom betrachtet wird, entspricht es der 1. Maxwellschen Gleichung in der Integralform.

Magnetisierungskennlinie B=f(H)

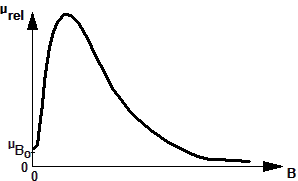
• Beim Auf- bzw. Abmagnetisieren von Eisen entstehen Schleifen der Magnetisierungskurve, deren Breite von der Aussteuerung in den Umkehrpunkten abhängt. Bei großen H-Werten tritt keine zusätzliche, durch das Material bedingte B-Erhöhung mehr ein (Sättigung).
• Für die Modellierung ist die Nachbildung der Magnetisierungshysterese meist zu aufwändig. Für viele Anwendungsfälle genügt die Nachbildung der Neukurve, welche praktisch mit dem Verlauf der Kommutierungskurve übereinstimmt. Es besteht dann ein eindeutiger Zusammenhang zwischen der Flussdichte B und der Feldstärke H, der über eine Funktion µ_rel=f(B) dargestellt werden kann:

Magn. Spannung [V] = A

• _Umlauf∫H·ds = Θ = ΣV_x - unterteilt man den Umlaufweg in einem magnetischen Kreis in einzelne Abschnitte, so ist die Summe aller magn. Spannungen der einzelnen Abschnitte gleich der MMK dieses Umlaufweges.
• V_AB = _A-B∫H·ds - die magn. Spannung zwischen zwei Punkten des magn. Kreises ergibt sich aus dem Weg-Integral der Feldstärke zwischen diesen beiden Punkten

Magn. Widerstand [Rm_AB=V_AB/Φ] = A/(V·s)

• In Analogie zum elektrischen Widerstand kann man einen magnetischen Widerstand zwischen zwei Punkten eines magnetischen Kreises definieren.
• Ein Abschnitt des Raumes wird somit auf ein idealisiertes Element mit konzentrierten Parametern reduziert.
• Mit Hilfe der Netzwerkanalogien kann man damit das Verhalten des magnetischen Kreises simulieren.
• Rm=L/(µ·A) - im homogenen Feld gilt für prismatische Raumabschnitte der Länge L und dem Querschnitt A (z.B. Zylinder, Quader) die Dimensionierungsgleichung.
• Für komplexere Teil-Geometrien eines magnetischen Kreises existieren teilweise zugeschnittene Dimensionierungsgleichungen (z.B. für Kugel- und Zylinderschalen).
• Der "exakte" magnetische Widerstand von komplexen Magnetkreis-Abschnitten lässt sich oft nur mit der Methode der Finiten Elemente ermitteln.
• Gm=1/Rm - der magnetische Leitwert besitzt die Einheit H=V·s/A.
• L=w²·Gm - Der gesamte magnetische Leitwert eines magnetischen Kreises ist proportional der elektrischen Induktivität L der Spule mit der Windungszahl w.

Kraftwirkung des Elektromagneten

In Abhängigkeit von möglichen Idealisierungen des magnetischen Feldes kann man unterschiedliche Verfahren nutzen, um die Kraftwirkung auf Grenzflächen innerhalb des magnetischen Kreises hinreichend genau zu berechnen:

Energieänderung (Induktivität)

• F=0,5·i²·(dL/ds) - betrachtet man die Energieänderung in der elektrischen (Ersatz-)Induktivität bei Änderung ds des Arbeitsluftspalts s, so erhält man eine Formel, nach der die Kraft proportional der Ableitung der Induktivität nach dem Luftspalt ist.
• Der Proportionalitätsfaktor ist das Quadrat des elektrischen Stroms i.
• Ist dL/ds für einen vorgegeben Luftspalt bekannt, so kann man für "beliebige" Ströme die Kraft berechnen (unter der Annahme, dass dL/di=0, d.h. die Induktivität ist "hinreichend" unabhängig vom Spulenstrom.
  

Maxwellsche Zugkraftformel

• Unter der Annahme, dass an der Grenzfläche A sehr große µ-Unterschiede existieren und ein homogenes Feld der Flussdichte B hindurchgeht, gilt die Maxwellsche Zugkraft-Formel F=A·B²/(2·µ₀)

Maxwellsches Stress Tensor Volumenintegral

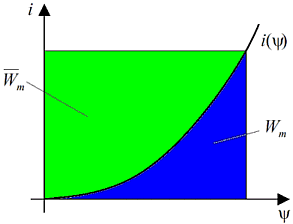
• Für den allgemeinen Fall des inhomogenen Feldes durch einen Körper mit anderem µ als seine Umgebung, kann man die resultierende Kraft durch Aufintegration aller differentiell kleinen Kraftanteile über seine Oberfläche gewinnen.
• Grundlage der Kraftberechnung ist die differentielle Änderung der magnetischen Coenergie [math]\displaystyle{ \overline{W} }[/math]_m bei differentieller Verrückung der Oberfläche (Ψ=Verkettungsfluss).

← →