Software: FEM - Tutorial - Elektrostatik - Modellbildung

↑

← →

Modellbildung

Für die Domäne "elektrostatisches Feld" werden folgende Zusammenhänge als bekannt vorausgesetzt:

• "Dimensionierungsgleichung" für einen Kondensator bei homogenen Feld: C=ε·A/d
• "Definitionsgleichung" für die Kapazität: C=Q/U

In dieser Übung wollen wir das erworbene Wissen zur Modellbildung weitestgehend selbstständig anwenden. An dieser Stelle noch einige Hinweise:

Idealisierungen:

• Modellieren muss man nur die obere Hälfte der Leiterplatte (inklusive der Masse-Ebene).
• Wir nutzen die Symmetrie-Eigenschaften der Geometrie und des elektrostatischen Feldes (z.B. nur Modell der rechten Hälfte).
• Wir verwenden 2D-Elemente (Membran). Günstig ist eine "Dicke" der Elemente von 1 m, dann erhält man die berechnete Kapazität sofort als Kapazitätsbelag pro Meter. Die "Dicke" entspricht im Modell der betrachteten Leiterzuglänge.
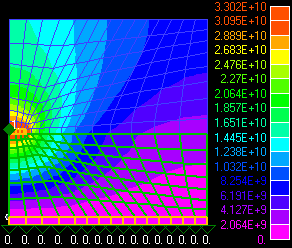
• Die Kapazität zwischen Leiterbahn und Masse-Ebene wird durch das gesamte elektrostatische Feld bestimmt:
  • Dieses erstreckt sich theoretisch durch den unendlichen Raum.
  • Praktisch genügt jedoch der Raum in der Nähe des Leiters. Die Breite dieses Bereiches neben der Leiterbahn sollte mindestens so groß sein wie der Abstand des Leiters zur Masse-Ebene.
  • In geringerem Maße trägt auch das Feld über dem Leiter (durch die Luft) mit zur Kapazität bei. Dieser Luftraum sollte deshalb im Modell berücksichtigt werden.

Planung der Vernetzung:

• Grundlage sind die Materialbereiche, der erwartete Feldverlauf und die mögliche Knoten-/Elementzahl.
• An den Stellen mit der größten Feldstärke (größter Gradient des Potentialfeldes) sollte die Vernetzung am Dichtesten sein. Dies betrifft vor allem den Bereich um die Leiterbahn, insbesondere an den Ecken.
• In den Randbereichen (geringe Feldstärken) kann das Netz gröber sein.
• Für die Kupferschichten genügt jeweils eine Elementschicht. Die Kupferelemente könnten prinzipiell auch weggelassen werden. Es würde auch die Belegung der Ränder zum Kupfer mit einer konstanten Spannung genügen. Aus Gründen der Anschaulichkeit werden wir das Kupfer auch modellieren.

Tipps zur Vernetzung:

Wir werden wieder mittels des Mapped Mesher ein Netz aus Quad-Elementen aufbauen. Dafür ist Voraussetzung die Unterteilung des Gesamtnetzes in günstige viereckige Teilnetze.

• Die Grenzen zwischen unterschiedlichen Materialien müssen zu Grenzlinien zwischen unterschiedlichen Teilflächen werden. Deshalb sollte man zuerst alle rechteckigen Material-Bereiche mit Rechtecken umranden. Im Beispiel sind dies:
  • das FR4-Material,
  • die Cu-Massefläche und
  • der Cu-Leiterzug.
  • Der Luftbereich muss aus mehreren Rechtecken zusammengesetzt werden.

Hinweis: Nach der material-orientierten Unterteilung in Rechtecke sollte man mittels (Tools > Check) coincidente Linien und Punkte zusammenfassen (übereinander liegende Rechteckseiten!)

• Engere Vernetzung an kritischen Stellen lässt sich über die Angabe eines Bias-Faktors für einzelne Linien realisieren:
  • Dazu müssen an den kritischen Stellen des Netzes jedoch Ecken von Teilflächen liegen.
  • Kritisch sind die Ecken des Leiterzuges, weil dort die größten Feldstärken auftreten.
  • Zusätzlich zur material-orientierten Unterteilung ist deshalb eine weitere vernetzungsorientierte Zergliederung in Vierecke erforderlich.

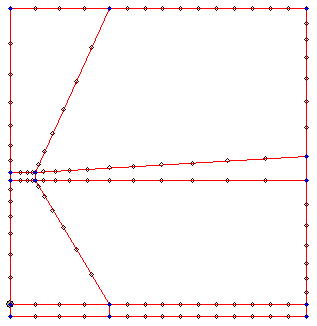
Das folgende Bild zeigt eine Möglichkeit der Zergliederung in Teilflächen und der Vernetzungssteuerung für die Kanten:

• Die Erzeugung schräger Grenzlinien zwischen den Flächen ist sehr einfach durch nachträgliches (Modify > Edit > Point) der ursprünglichen Endpunkte von Rechtecken.
• Bei der Vernetzungssteuerung sollte man in Hinblick auf die 300 Knoten der Demo-Version ca. 10% Reserven lassen, damit die Vernetzung selbst noch realsierbar bleibt.
• Im Sinne der Übersichtlichkeit ist es günstig, mittels der View Options <F6> für die Elemente als Farbe (der Elementränder) die Materialfarbe anzuzeigen. Den Materialien sollten wir zuvor sinnvolle Farben und Linienstärken zuordnen. Die Linienstärke wird Bestandteil der "Farb-Eigenschaft".

Ein mögliches Problem:

• In der FEMAP-Version 9.1 gelang es häufig nicht, aus den 4 Linien, welche die Kupferfläche des Leiterzuges umranden, eine Boundary Surface zu bilden! Scheinbar werden auf Grund von Rundungsfehlern infolge der sehr kleinen Koordinatenwerte bei der Bildung der Boundary Surface falsche Linien zugeordnet (es entstehen "chaotische" Linienzüge).
• Falls dieser Fall auch in der aktuellen FEMAP-Version auftritt, sollte man für den Bereich des Kupfer-Leiters anstatt der Boundary Surface eine "normale" Surface verwenden (Geometry > Surface > Corners). Die anschließende Vernetzung funktioniert genauso, wie bei den Boundary Surfaces.
• Hinweis: Surfaces sind standardmäßig durch eine Gitter-Schraffur gekennzeichnet. Hierbei handelt es sich nicht um Elemente des FE-Netzes!

Den Prozess der Vernetzung kann man im Vergleich zu unseren ausführlichen Schritten in der ersten Übung stark rationalisieren:

• Das Zuweisen des "Mapped Mesher" kann man für alle Boundary Surfaces gleichzeitig vornehmen (Mesh > Mesh Control > Approach On Surface > Select All).
• Da es sich bei den Surfaces bereits um Vierecke handelt, muss man die 4 Eckpunkte nicht angeben.
• Nur wenn beim Vernetzen kein "Mapped Mesh" entsteht, ist es erforderlich für die einzelne Teilfläche (Mesh > Mesh Control > Size On Surface) auszuführen.
• Gleiche Material-Teilflächen sollte man grundsätzlich gleichzeitig Vernetzen.

Load und Constraint:

• Leider wird in FEMAP nicht konsequent der theoretische Ansatz entsprechend der Analogiebeziehungen umgesetzt.
• Constraint sind hier nur für die mechanische Domäne definierbar (Einschränkung der Knotenbeweglichkeit).
• In der thermischen Domäne (als implementierter Stellvertreter für Potential-Probleme) muss man eine Vorgabetemperatur (Spannungsvorgabe im elektrostatischen Bereich) mittels "Load" definieren.
• Wir wollen die Masse-Ebene mit dem elektrischen Potential 0 V versehen (Load Nodal auf alle Knoten unter der Masse-Ebene). Unter Nutzung der Analogie verwenden wir statt der Spannung eine Temperatur von 0 K.
• Die Leiterbahn muss eine Ladungsmenge erhalten. Am Anfang geben wir 1 As vor (Load Nodal für einen Knoten der Leiterbahn). Unter Nutzung der Analogie verwenden wir statt der Ladungsmenge eine Wärmestromquelle (Heat Flux).
• Wichtig:
  Damit der Means-Solver die Modellberechnung nicht verweigert, muss man bei Potentialproblemen einen leeren Constraintset im Modell definieren!

← →