Software: FEM - Tutorial - Diskretisierung - Elementformen
Unsere Welt lässt sich in eine Objekt-Hierarchie gliedern, deren einzelne Objekte wir als Kontinuum betrachten können ( solange wir uns nicht in atomare Strukturen hinunter begeben). Wir können (mit etwas Idealisierung) Objekte unterschiedlicher räumlicher Dimension unterscheiden:
- 1-dimensional: Linienobjekte (z.B. Fäden) mit Anfangs- und Endpunkt
- 2-dimensional: Flächenobjekte (z.B. Membranen) mit Randlinie und -punkten
- 3-dimensional: Volumenobjekte (z.B. Quader) mit Mantelflächen, Kanten und Eckpunkten
Grenzen wir ein homogenes Teilsystem ab (z.B. aus einem einheitlichen Stoff bestehend), so lässt sich die Energiebilanz solch eines Teilsystems als partielle Differentialgleichung beschreiben. Der Zustand jedes Punktes dieses Kontinuums ist Funktion:
- eines Anfangszustandes,
- der verflossenen Zeit und
- der Wechselwirkung mit der Umgebung.
Für Spezialfälle lassen sich auf dem Niveau des Kontinuums diese Ansatzfunktionen (partielle DGL) formulieren und analytisch lösen (nur für einfachste Geometrien!). Um auch das Verhalten komplexerer Objekte numerisch berechnen zu können, geht man den Weg der Diskretisierung, d.h. man reduziert das Kontinuum auf die Behandlung endlich vieler Punkte.
Die Methode der Finiten Elemente (FEM) ist ein Weg zur Diskretisierung:
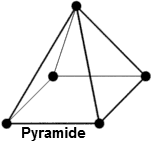
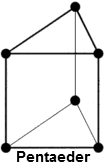
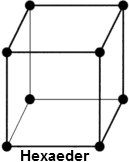
- Reduktion auf geometrisch einfache Formen, die über wenige Eckpunkte definiert sind:
- 1-dimensional:
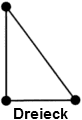
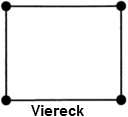
- 2-dimensional:
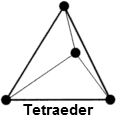
- 3-dimensional:
- Diese geometrischen Grundformen können in beliebig verzerrter Form benutzt werden. Dabei wird die Größe der zulässigen Verzerrung jedoch bestimmt durch die Gradienten der Spannungen (Gradienten des Potentialfeldes). So führen sehr spitze Winkel bzw. sehr schlanke Formen oft zu ungenauen Ergebnissen.
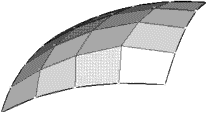
- Mit diesen geometrischen Grundformen werden z.B. gekrümmte Oberflächen durch Facetten ebener Teilflächen angenähert (Siehe oberstes Bild).
- Elemente erhalten in der Literatur üblicher Weise einen Kurzbezeichner, welcher sich aus ihrer geometrischen Form und der Anzahl ihrer Knoten ableitet (Zusätzlich zu den Eck-Knoten sind je nach gewählter Ansatz-Funktion weitere Knoten auf den Kanten bzw. in den Elementen erforderlich):
| geom. Form | nur Eck-Knoten | mit Zusatz-Knoten |
|---|---|---|
| Dreieck | TRIA3 | TRIA6 |
| Viereck | QUAD4 | QUAD8 / QUAD9 |
| Tetraeder | TETRA4 | TETRA10 |
| Pyramide | PYRAM5 | PYRAM13 |
| Pentaeder | PENTA6 | PENTA15 |
| Hexaeder | HEX8 | HEX20 |