Software: FEM - Tutorial - Diskretisierung - Ansatzfunktionen

↑

← →

Ansatzfunktionen

Grundlagen

• Für die jeweilige Elementform werden nur die Potential-Werte ihrer Knoten-Punkte als so genannte Primär-Ergebnisse berechnet.
• Zusätzlich muss nun eine geeignete Funktion definiert werden, welche es ermöglicht, aus diesen Knoten-Potentialen für alle Punkte innerhalb des Elements einen eindeutigen (und sinnvollen) Wert zu berechnen (Sekundär-Ergebnisse).
• Man kann sich die Knoten als Stützstellen dieser Funktion vorstellen.
• Diese Funktion definiert man für Finite Elemente auf der Basis von Ansatzfunktionen.
• Von einer "Ansatzfunktion" spricht man, wenn sie folgende Bedingungen erfüllt (Nach [1]):

1. Die Funktion ist auf dem ganzen Element definiert.
2. Jedem Knoten des Elements ist eine Funktion zugeordnet.
3. Am Knoten hat diese Funktion den Wert=1, an allen anderen Knoten des Elements hat sie den Wert=0.
4. Für jeden Punkt des Elements hat die Summe aller Funktionen den Wert=1.
5. An gemeinsamen Kanten (oder Flächen) zu benachbarten Elementen haben die Funktionen gemeinsamer Knoten an jedem Punkt den gleichen Wert (Stetigkeit).

• Üblich für den Begriff "Ansatzfunktion" sind auch:
  • Formfunktion (eng. form-function / shape-function)
  • Interpolationsfunktion (engl. interpolation-function)
  • Näherungsfunktion

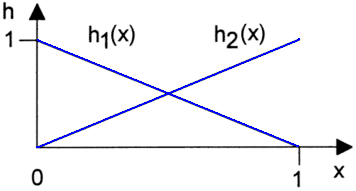
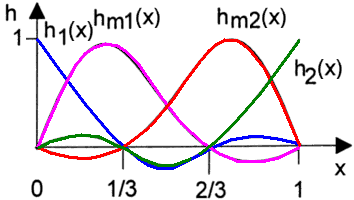
Dies soll am Beispiel eines 1-dimensionalen Elements der Länge=1 für lineare Ansatzfunktionen verdeutlicht werden:

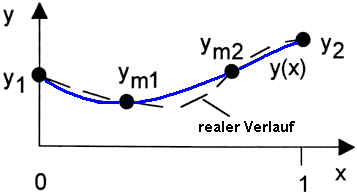
• Gegeben sind die Funktionswerte y₁ und y₂ an den Knoten des Stabes.
• Es werden zwei Ansatzfunktionen definiert

h₁(x)=1-x

h₂(x)=x

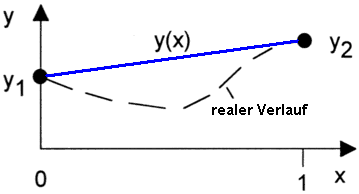
• Gewichtet mit den Knotenwerten y₁ und y₂ lautet die Elementfunktion

y(x)=y₁·h₁(x)+y₂·h₂(x)

y(x)=y₁·(1-x)+y₂·x

Analog ist die Vorgehensweise bei höherwertigen Ansatzfunktionen:

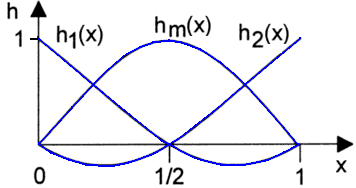
• Quadratische (=parabolische) Ansatzfunktionen erfordern in der Mitte des Stabes einen zusätzlichen Knoten.
• Es werden für den Stab drei Ansatzfunktionen entsprechend der Knotenzahl gebildet.
• Diese sind so formuliert, dass Sie obigen Bedingungen genügen.

• Kubische Ansatzfunktionen erfordern zwei Zwischenknoten auf dem Stab:

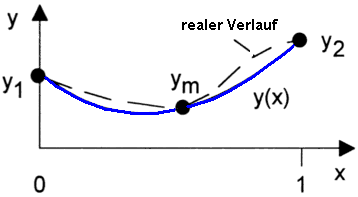
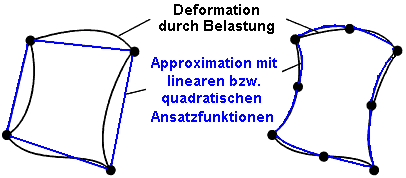
Je höherwertig die gewählte Ansatzfunktion ist, desto besser gelingt die Annäherung der interpolierten Werte an den realen Verlauf der physikalischen Größen. Dies betrifft sowohl die Spannungen (Potentiale) als auch die mechanischen Verformungen der Elemente unter Belastung. Allerdings steigt mit der erforderlichen Knotenzahl auch die Zeit für die Modellberechnung.

In der Praxis beschränkt man sich auf lineare und insbesondere quadratische Ansatzfunktionen. Zur Erreichung einer höheren Genauigkeit wählt man statt einer höheren Ansatzfunktion eine engere Vernetzung!

Für Spezialanwendungen haben sich neben den obigen Polynomansätzen weitere Ansatzfunktionen etabliert:

• Realisierung weicher Übergänge an den Elementgrenzen (ohne Knick), d.h. stetige Differenzierbarkeit auch über die Grenzen hinweg.
• trigonometrische Funktionen
• Im Element=konstant (Treppe über die Elemente) für schnell zu berechnende, riesige Netze (Strömungs- und Crash-Simulationen).
• usw. ...

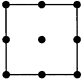
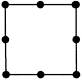
Höherwertige Ansatzfunktionen erfordern auf den Elementen zusätzlich zu den Eck-Knoten noch Zwischenknoten auf den Kanten bzw. innerhalb der Elemente. Dies soll am Beispiel der quadratischen Ansatzfunktion für das Viereck-Element verdeutlicht werden:

• Der normale Polynom-Ansatz erfordert 5 zusätzliche Knoten.
• Der heute übliche Lagrangesche Ansatz benötigt den Innenknoten nicht.
• Ein unter Belastung verformtes Viereck kann mit seinen gekrümmten Kanten bei Verwendung von Zwischenknoten besser approximiert werden:
  

[1] Steinbuch: Finite Elemente - ein Einstieg S.38

Springer-Verlag Berlin Heidelberg New York

ISBN 3-540-63128-3

Wirkung bei der Modellberechnung

• Die verwendeten Ansatzfunktionen fließen vollständig ein in das Gleichungssystem zur Berechnung der Knoten-Potentiale.
• D.h., je höherwertig die Ansatzfunktion gewählt wird, desto besser ist zwischen den Knoten die Approximation an die realen Potentialverläufe (Verschiebungen in der Mechanik).
• Man kann demzufolge gleiche Genauigkeiten mit einer gröberen Vernetzung erzielen. Diesem Vorteil wirkt jedoch die höhere Anzahl von Knoten pro Element wieder entgegen.
• Die benötigte Zeit für die Lösung des Gleichungssystems steigt quadratisch mit der Zahl der Unbekannten, welche proportional mit der Knotenanzahl steigt:
  • Für Potentialprobleme wird nur eine Unbekannte pro Knoten berechnet, in der Mechaniksimulation sind es 1 bis 6 Unbekannte (abhängig von den berücksichtigten Freiheitsgraden).
  • Demzufolge hat man bei Potentialproblemen mehr Spielraum für eine feinere Vernetzung.
  • Im Sinne der benötigten Berechnungszeit haben sich quadratische Ansatzfunktionen mit einer entsprechend feinen Vernetzung als optimal erwiesen.

← →