Software: FEMM - Elektrostatik - Open Boundary Problems

↑

← →

Open Boundary Problems

Die Finite Element Methode setzt die Verwendung eines endlichen Netzes voraus. Mit dem Netz kann also nur ein abgegrenzter Raumbereich mittels partieller Differentialgleichungen modelliert werden. Nun existieren aber viele Feldprobleme, bei denen das Ergebnis der Simulation wesentlich von der Ausbreitung des Feldes im "unendlichen" Raum abhängt:

• Das Streufeld einer Magnetspule bestimmt wesentlich die Induktivität.
• Der elektrische Widerstand oder die elektrische Kapazität zwischen weit voneinander entfernten Elektroden wird wesentlich durch die Ausbreitung des elektrischen Feldes bestimmt.

Hinreichend großes FE-Netz:

• Diese einfachste Methode zur Berücksichtigung des "unendlichen" Raumes haben wir im Modell Leiterplatte1_xx angewendet.
• Hinreichend weit von der eigentlichen Objektgeometrie entfernt zieht man eine Grenze.
• Diese Grenze muss so weit entfernt sein, dass die Anteile des Feldes außerhalb der Grenze vernachlässigt werden können.
• Ein Richtwert besagt, dass diese Grenze mindestens 5-Mal so weit vom Zentrum der Objektgeometrie entfernt sein soll, wie der maximale Abstand der Objektränder von diesem Zentrum.
• Für diese Grenze ist dann automatisch definiert, dass z.B. für das elektrostatische Feld die Äquipotentiallinien senkrecht auf diesen Rand treffen.
• Damit existiert kein Feld außerhalb der Grenzen!

Open Boundary Conditions:

• Über Randbedingungen kann man definieren, welche Wirkung der Raum außerhalb der Grenzen auf das Feld innerhalb der Grenzen ausüben soll.
  
• Im Beispiel wollen wir den "unendlichen" Luftraum nachbilden, in den sich das Streufeld der Leiterbahn erstreckt.
• Die richtigen Randbedingungen sind entscheidend für die Genauigkeit der Modellberechnung.
• Sowohl die Geometrie der Grenze als auch das konkrete Feldproblem muss man bei der Formulierung der Zwangsbedingungen für den Feldverlauf beachten.
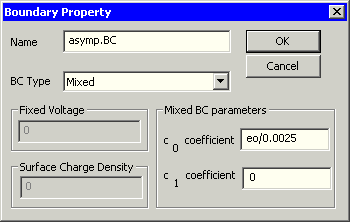
• In FEMM wird dafür als "Boundary Property" der Boundary Condition Type "Mixed" bereitgestellt:
  • Dieser setzt als Grenzgeometrie den Kreis voraus (entspricht der Kugel im axialsymmetrischen Fall).
  • Die Koeffizienten der Zwangsbedingung berechnet man anhand der konkreten Geometrie und der Art des Feldproblems.

Mit einem neuen Modell Leiterplatte2_xx werden wir nun diese anspruchsvollere Methode für die Berücksichtigung des "unendlichen" Raumes verwenden:

• Wir speichern unser bisheriges Modell unter dem neuen Namen.
• Die interessierende Geometrie (Leiterbahn) muss näherungsweise im Zentrum des Kreises liegen.
• Es gilt für den Radius der Sphäre hier ebenfalls der Richtwert vom 5-fachen Wert des Objekt-Radius.
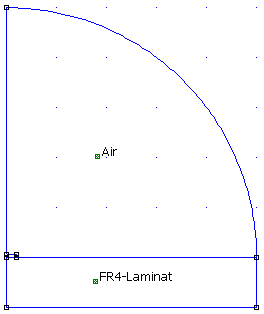
• Wir ersetzen den rechteckigen Luftraum durch einen 90°-Kreisbogen mit einem Radius von 2.5 mm:
  • Markieren der zu löschenden Knoten und Löschen mit <Entf>.
  • Dabei werden daran hängende Linien-Segmente ebenfalls gelöscht.
  • Das Block-Label "Air" bleibt dabei erhalten.
  • Verändern der Laminat-Breite durch Verschieben von Laminat-Knoten auf x=2.5 mm.
  • Kreisbogen zwischen Endpunkt Laminatoberfläche und Knoten auf der y-Achse.
• Die Randbedingung muss zuerst definiert werden, bevor man sie dem Kreisbogen zuweisen kann:
  • Über Properties - Boundary fügt man mittels Add Property eine neue Randbedingung hinzu.
  • Der Name ist frei wählbar, z.B. "Asymp.BC"
  • Wir wählen den Boundary Condition Type "Mixed"

• Die Eingabefelder für c_o und c₁ gehören zu einer Formel, welche den Potentialverlauf an der Grenzfläche beschreibt:
  
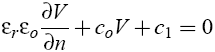
  • c₁=0 darf hier nicht verändert werden.
  • ε_r für Luft ist 1
  • ε_o=8.85418781762e-012 As/Vm
  • c_o berechnet man für Luft aus Permittivität ε_o, dem Radius r_o der Grenzsphäre und einem Faktor n, welcher Problemabhängig ist:
    
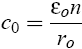
  • Für n gilt in der Elektrostatik:
    • n=1: planares Problem mit Dipol-Ladungsverteilung in der Geometrie. Das bedeutet, die Geometrie erscheint aus großer Entfernung als ladungsloser "Punkt".
    • n=1: axialsymmetrisches Problem mit Netto-Aufladung der Geometrie. Das bedeutet, die Geometrie erscheint aus großer Entfernung als Punktladung.
    • n=2: für die beiden anderen Problem-Varianten
  • Wir müssen für unser Beispiel n=1 benutzen!
  • In Form der Lua-Scriptsprache von FEMM tragen wir für c_o einen Ausdruck ein:
    • Dabei muss man unabhängig von der gewählten Maßeinheit des Problems [mm] den Wert des Radius r_o=2.5 mm in [m] angeben:
      eo/0.0025
    • eo steht für den Wert der Permittivität ε_o.
  • Nach dem Schließen des Dialogfensters werden die Ausdrücke in den Wert-Eingabefeldern berechnet und durch den resultierenden Zahlenwert ersetzt. D.h., beim nächsten Aufruf dieses Property-Dialogs (z.B. zum Modifizieren), wird der ursprüngliche Ausdruck nicht mehr angezeigt!
    
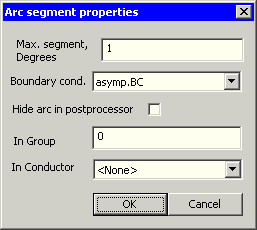
• Diese Randbedingung soll nun der Grenzfläche zugewiesen werden:
  • Man muss in den Kreissegment-Modus wechseln und den zugehörigen Viertelkreis auswählen durch Anklicken mit der rechten Maustaste.
  • Nach Betätigen der Leertaste gelangt man in den Dialog, der die Zuordnung der Randbedingung gestattet.

Der weitere Prozess verläuft nun wie im vorherigen Modell:

• Sämtliche Properties einschließlich der Vernetzungsparameter müssten noch vom Vorgänger-Modell erhalten sein.
• Die Simulation sollte ziemlich exakt den gleichen Kapazitätsbelag ergeben, wie mit dem vorherigen Modell.
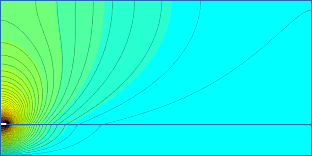
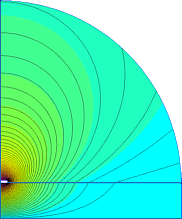
• Allerdings unterscheidet sich bei genauerem Vergleich der Feldverlauf in der Luft in größerer Entfernung von der Leiterbahn:

• Die gewählte Randbedingung beschreibt die Verhältnisse des Streufeldes wesentlich besser!

Beachte:

• Die bedeutend größere Ausdehnung des Laminats (nach "rechts") wird im Beispiel nicht durch die asymptotische Randbedingung berücksichtigt!
• Die Feldlinien gehen dort senkrecht durch den Netzrand, der dadurch resultierende Fehler ist jedoch praktisch nicht spürbar.

Frage für Teilnehmer der Lehrveranstaltung:

• Gegen welchem Betrag konvergiert der Wert für den vollständigen Kapazitätsbelag einer Leiterbahn in Bezug auf die Masse-Ebene im FEMM mit diesem Modell-Ansatz?
• Senden Sie das mit diesen Werten konfigurierte Modelldatei Leiterplatte2_xx.FEE als Teil der Lösung.
• Die Datei *.res ist wieder sehr groß und sollte nicht mitgeschickt werden. Die Ergebnisse sind aus der Modelldatei jederzeit reproduzierbar!

← →