Software: CAD - Tutorial - Dynamik - Simulation

↑

← →

Dynamik-Simulation

Vor dem Start der Simulation sollte man eine definierte, sinnvolle Ausgangslage der beweglichen Komponenten einstellen (Siehe Bild):

• Ankerhals anliegend am rechten Anschlag
• Ellipse der Unruhe in einer Position rechts oberhalb der Ankergabel
• Hemmungsrad in Stopp-Position (Zahn anliegend an rechter Ankerpalette

Startet man die Simulation über einen Zeitbereich von 3 s mit 300 Schritten, so wird es für diese beispielhafte Ausgangslage infolge von Prellvorgängen sehr schnell zu einem Verklemmen des Mechanismus kommen:

Simulation der Schweizer Hemmung
Flash-Animation

Grafische Animation

Hinweis:
Damit die Konturen der Bauteile in der grafischen Darstellung besser hervortreten, solte man MFL > Ansicht > Visueller Stil > Schattiert mit verdeckten Kanten wählen.

In Abhängigkeit von der individuell gewählten Auslenkung der Unruhe kann es zum Verklemmen des Ankers zwischen Hemmungsrad und Unruhe-Palette kommen:

• Im animierten Simulationsbeispiel kann man dieses Verklemmen beobachten. Die Verklemm-Position ist im obigen Bild dargestellt.
• Im Vergleich dazu sollte man das ideale Verhalten einer Schweizer Hemmung analysieren.
• Der wesentliche Unterschied zwischen dynamischer Simulation und idealisierter Kinematik besteht im Auftreten starker Prellvorgänge an allen 2D-Kontaktstellen. Insbesondere das Prellen des Ankers an den Anschlägen führt anscheinend zum Verklemmen des Ankers bei der Dynamik-Simulation und sollte im Weiteren näher betrachtet werden.
• Die grafische Animation der Bewegung ist sehr "anschaulich" (im wahrsten Sinne des Wortes). Sie gestattet jedoch trotz der Nutzung des Schrittbetriebs nur eine qualitative Analyse der Vorgänge an den Kontaktstellen.

Ausgabediagramme

Eine detailierte quantitative Analyse des Verhaltens ist nur auf der Basis ausgewählter Signalverläufe f(t) möglich (Wege, Geschwindigkeiten, Kräfte usw.). Dafür kann man beliebig viele Ausgabediagramme öffnen.
Hinweis: Die folgenden Diagramme zeigen die Bewegungsvorgänge von einer anderen Ausgangslage:

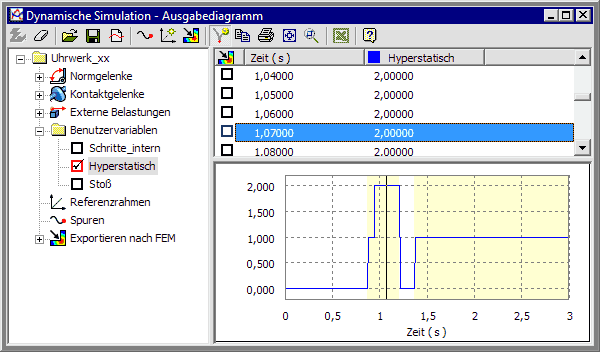
• Im Beispiel fällt auf, dass Bereiche des Diagrammfensters farblich hinterlegt sind.
• Wir stellen von den vordefinierten Benutzervariablen den Verlauf von Hyperstatisch dar. Nun wird deutlich, dass in diesen farblich markierten Zeitbereichen das Dynamik-Modell einen "hyperstatischen" Zustand besitzt.
• "Hyperstatisch" ist eine schlechte Eindeutschung von Hyperstatic = statisch unbestimmt. Da dynamische Systeme nicht unterbestimmt sein können, handelt es sich hier um einen überbestimmten Zustand.
• Im Diagramm wird der Wert der statischen Überbestimmtheit angezeigt. Ein Wert>0 bedeutet praktisch, dass gleichzeitig so viele Kontaktstellen im Eingriff sind, dass sich der simulierte Mechanismus durch zusätzliche Wirkung der Reibung "verklemmen" könnte.

Wählt man mittels Doppelklick im Diagrammfenster einen bestimmten Zeitpunkt, so wird der zugehörige Zustand in der grafischen Animation angezeigt. In der Wertetabelle des Ausgabediagramms wird die zugehörige Wertezeile markiert dargestellt:

• Ausgehend vom aktuell gewählten Zeitpunkt kann man sich mit den Pfeiltasten schrittweise nach links oder rechts bewegen.
• Alle geöffneten Diagrammfenster arbeiten zeitlich synchron.

Bewegung der Normgelenke

Nach Inaktivieren der Variablen "Hyperstatisch" stellen wir im Diagrammfenster für die Hemmungskomponenten die Winkelgeschwindigkeiten [grd/s] dar:

• Für die Normgelenke werden die Bewegungsgrößen (Positionen, Geschwindigkeiten, Beschleunigungen) und Lager-Reaktionen (Kräfte, Momente) berechnet.
• Je nach Art des Gelenks handelt es sich bei den Bewegungsgrößen um translatorische bzw. rotatorische Größen. In unserem Beispiel des Drehgelenks gibt es nur rotatorische Bewegungsgrößen in Bezug auf die Drehachse:

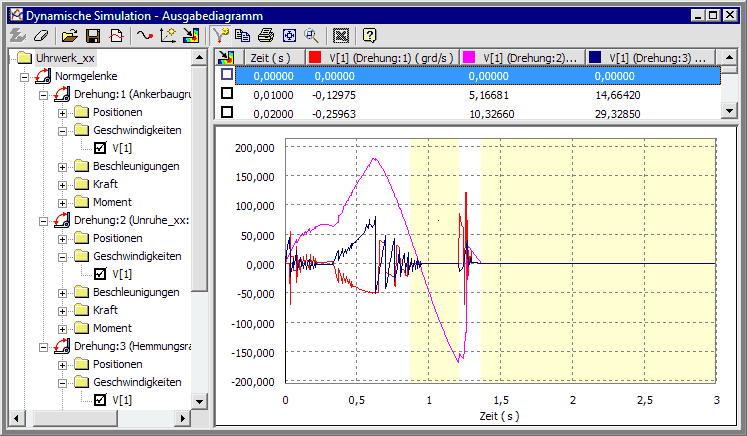
• Man erkennt, dass überbestimmte Zustände auftreten, wenn mindestens ein Normgelenk zur Ruhe kommt.

Kontakte (in Kontaktgelenken)

Ursache der Bewegungsänderungen sind die auf die starren Körper (Trägheiten) wirkenden Kräfte. In unserem Beispiel sind dies vor allem die Kontaktkräfte (in den Kontaktgelenken) zwischen den starren Körpern. Diese Kontaktkräfte entstehen nur, wenn sich die betreffenden Kontakte an mindestens 1 Punkte berühren.

Anstatt der Kontaktkräfte schauen wir uns vorerst nur die Berührungsvorgänge an. Dazu stellen wir in einem weiteren Diagramm den Status der Kontakt-Berührung dar:

• Ein 2D-Kontaktelement kann sich maximal an 3 Punkten gleichzeitig berühren. Für jeden dieser Punkte stehen die Kontaktkräfte und der Kontakt-Status als Werte zur Verfügung.
• Ob und wie eine Berührung in einem Kontaktpunkt stattfindet, widerspiegelt sich im Wert der Status-Variablen.
• In unserem Beispiel kann es nur kurzzeitig zu einer 2-Punkt-Berührung zwischen der Unruhe-Ellipse und der Anker-Gabel kommen. In der im folgenden Bild dargestellten Simulation tritt keine 2-Punkt-Berührung auf:

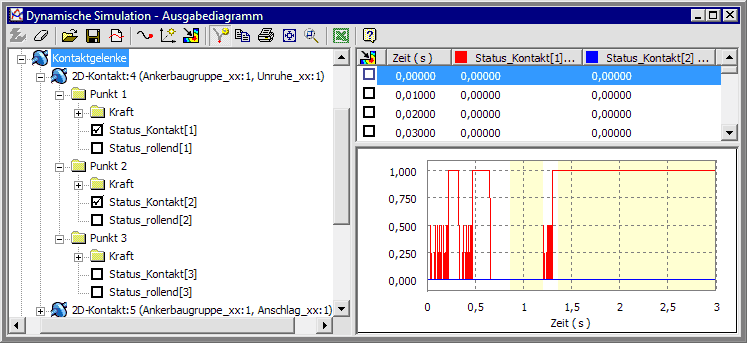
• Kontaktstatus (Berührung):
  • 0  = keine Berührung
  • 1  = dauerhafte Berührung
  • 0,5= im nächsten Schritt erfolgt Lösen des Kontakts (z.B. Abprall)
• Schiebestatus (Gleiten bzw. Rollen in Bezug auf Gelenkkoordinatensystem:
  •  0  = Gleiten entlang der X-Achse
  •  -1 = Gleiten entgegen der X-Achse
  • +1 = Abrollen der Kontaktflächen ohne Gleiten
• Die Z-Achse des Gelenkkoordinatensystems entspricht dem Normalenvektor der Kontaktfläche im 2D-Gelenk. Die X-Achse ist also die Tangente an der 2D-Kontur. In diesem Sinne kann man die Werte von Status_rollend interpretieren:

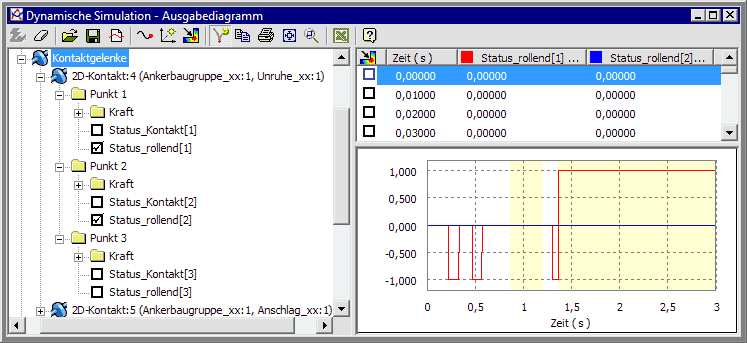
• Das Verklemmen des Mechanismus in der zweiten Hälfte der Simulationszeit ist im obigen Bild gekennzeichnet durch das "Abrollen ohne Gleiten", welches dem "Haften" der Ellipse auf der Ankergabel infolge der Haft-Reibung entspricht.

Simulationseinstellungen

Die vielen Prellvorgänge (Kontaktstatus=0,5) sind problematisch

1. Für die dynamische Simulation, welche hier nur mit sehr kleinen Integrationsschritten voranschreiten kann.
2. Für das Verhalten des Mechanismus insgesamt:

• Jeder Stoßvorgang ist verlustbehaftet (Stoßzahl<1). Bei einem Stoßzahl von 0.8 ist z.B. nach 10 Prellvorgängen praktisch die gesamte Bewegungsenergie vernichtet (0.8¹⁰)!
• Hier stellt sich im Sinne der Modellvalidierung die Frage, ob die simulierten Prellvorgänge in diesem Umfang in der Realität überhaupt auftreten! In unserem Beispiel erkennt man am realen Objekt zwar einzelne, kurze Prellungen, aber nicht in diesem Ausmaß.

Die Simulation der Stoß- und Reibungseffekte mittels numerischer Integration ist ein anspruchsvolles Problem. Sie erfordert häufig eine feinfühlige Konfiguration sowohl des Integrationsverfahrens als auch der Kontaktparameter.

Bevor wir uns der Validierung der geometrisch-stofflichen Kontakteigenschaften zuwenden, konfigurieren wir die Numerik im Sinne einer stabilen Simulation des Mechanismus:

In der aktuellen Version von Autodesk Inventor wird ein 5-stufiges Runge-Kutta-Verfahren mit automatischer Anpassung der Integrationsschrittweite verwendet.

• Im Dialogfenster der Simulationswiedergabe kann man den Zeitbereich der Simulation festlegen. Dieser beginnt bei 0 s und endet im Beispiel bei 3 s:

• Die Integrationsschrittweite stellt sich in Abhängigkeit von der kleinsten Zeitkonstante innerhalb des Mechanismus automatisch ein:
  • Unabhängig von dieser automatischen Schrittweite werden zu definierten Zeitpunkten die berechneten Werte in einer Wertetabelle abgelegt. Für jeden dieser Zeitpunkte steht dann für die grafische Animation ein Einzelbild zur Verfügung. Standardmäßig werden 100 Zeitpunkte/Sekunde gespeichert (aller 10 ms). Diese Speicherschrittweite sollte man nicht unnötig klein wählen, sondern so groß, dass die Signalverläufe durch mangelnde Punktdichte noch nicht verfälscht werden. Im Beispiel wurde der Standardwert nicht verändert.
  • Da die Darstellung der Bilder während der Simulation Rechenzeit benötigt, kann man über einen Filterwert n ein Intervall für die tatsächliche Bildanzeige festlegen (nur jedes n. Bild wird angezeigt).

Die Simulationseinstellungen ermöglichen eine weitere Anpassung der numerischen Integration an das konkrete Modell. Dazu muss man im zugehörigen Dialogfenster die erweiterten >> Einstellungen öffnen. Die Felder sind mit den Standardvorgaben belegt:

• Die Änderung der Werte ist nur im Konstruktionsmodus möglich:

Beachte:
Im Folgenden wird die Wirkung der verfügbaren Simulationsparameter erläutert und es erfolgen allgemeine Hinweise für die Wahl geeigneter Werte. Es sollte noch keine Verstellung der Standardwerte vorgenommen werden! Die konkrete Konfiguration der numerischen Integration für unser Modell wird erst im nachfolgenden Abschnitt beschrieben.

Lösungsgenauigkeit - hat direkten Einfluss auf den Solver für die numerische Integration:

• Ein Verkleinern des Vorgabewertes führt zu kleineren Integrationsschrittweiten und entsprechend größerer Berechnungszeit.
• Ein Vergrößern führt zu größeren Schrittweiten, kann aber zu Instabilitäten wegen mangelnder Berechnungsgenauigkeit führen.
• Den Wert der Lösungsgenauigkeit kann man vorsichtig verkleinern, wenn man Fehlermeldungen zur Lösungsstabilität erhält.

Mikromechanismus-Modell - erhöht die Lösungsgenauigkeit für "Mikromechanismen":

• Im Standardmodus können nur Massen > 1e-10 kg oder Trägheiten > 1e-16 kg/m² behandelt werden. Dies entspricht Abmessungen von > ca.1 mm. In unserem Beispiel genügt das bei Weitem.
• Der Mikromechanismus-Modus verschiebt diese Grenzen nach unten auf 1e-20 kg bzw. 1e-32 kg/m².

Baugruppengenauigkeit - wann werden Kontaktpunkte als geschlossen betrachtet:

• Standardmäßig erfolgt bei 1 µm Kontaktpunkt-Abstand die Umschaltung des Kontakt-Status. Dieser Umschalt-Zeitpunkt wird von der numerischen Integration als Ereignis behandelt und im Rahmen der möglichen Genauigkeit angesteuert.
• Beim Eintreten des Kontakt-Ereignisses werden entsprechend der Kontaktparameter mit den Formeln des Stoßvorgangs die Bewegungsgrößen neu berechnet. Danach wird mit den neuen Bewegungsgrößen die zeitkontinuierliche Integration fortgesetzt.
• Bei großen Mechanismen (>1 m) kann man diesen Abstandswert wegen der Rechenungenauigkeiten erhöhen (Faktor 10..100).
• Bei kleinen Mechanismen (<10 mm) kann man diesen Abstandswert verringern (Faktor 10..100)
• Bei Mikromechanismen (<1 mm) verwendet man den Mikromechanismen-Modus und verringert den Wert um den Faktor 1000..10000.
• Wir behalten im Beispiel den Vorgabewert von 1 µm.

Erfassungsgeschwindigkeit (Capture Velocity oder Erstellgeschwindigkeit):

• Diese Grenzgeschwindigkeit hilft dem Solver dabei, die Anzahl der kleinen Stöße zu beschränken, bevor länger dauernde Berührung zwischen den Kontaktpunkten eintritt.
• Wird bei einem plasto-elastischen Stoßvorgang die berechnete Abhebegeschwindigkeit kleiner als die Grenzgeschwindigkeit, so wird dieser Stoßvorgang als rein plastischer Stoß behandelt. Damit bleiben die Kontaktpunkte vorläufig zusammen. Dies entspricht eher dem realen Prellvorgang, der bei kleinen Amplituden sehr schnell zur Ruhe kommt. Eine "unendliche" asymptotische Annäherung an die Prellamplitude Null kommt bei realen Kontakstellen nicht vor!

Regulierungsgeschwindigkeit (Regularization Velocity):

• Dieser Grenzwert kennzeichnet den Übergang zwischen Haft- und Gleitreibung in der verwendeten Reibungfunktion. Dieser Parameter hat nur Auswirkung auf die tangentialen Kraftwirkungen zwischen den Kontaktpunkten (Reibkräfte):

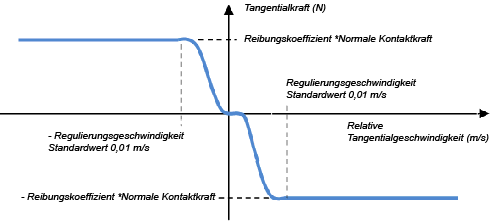
• Hinweis: Im obigen Diagramm wurde der Standardwert 10 mm/s für die Regulierungsgeschwindigkeit verwendet.
• Ist die Relativgeschwindigkeit kleiner als die Regulierungsgeschwindigkeit, so wirkt praktisch Haftreibung (Tangentialkraft=Antriebskraft, solange Haftkraft nicht überschritten). Bei größeren Relativgeschwindigkeiten ergibt sich die Tangentialkraft aus dem Produkt von Reibkoeffizienten und aktueller Normalkraft.
• Den Wert der Regulierungsgeschwindigkeit sollte man vorsichtig erhöhen (Faktor 5), wenn bei der Simulation kleine Schwingungen in einer Reibungsbehafteten Stelle auftreten und die Berechnung dabei sehr langsam voranschreitet. Der Wert der Regulierungsgeschwindigkeit sollte dabei aber kleiner sein, als die im konkreten Modell auftretenden Geschwindigkeiten.

Stabilisierung der numerischen Integration

In unserem Beispiel müssen wir die überflüssigen Kontaktprellungen vermeiden (Einzelwerte mit Kontaktstatus=0,5). Dazu genügt die Beobachtung des Kontaktstatus zwischen Unruhe-Ellipse und Anker-Gabel, z.B.:

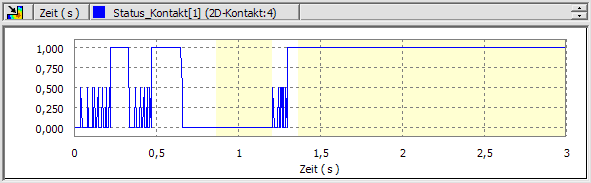
• Hierfür bietet sich eine Erhöhung der Erfassungsgeschwindigkeit an. Ziel sollte die Vermeidung direkt aufeinander folgender Prellvorgänge innerhalb der Ankergabel sein.
• Wir erhöhen dazu "vorsichtig" diese Grenzgeschwindigkeit und beobachten die nachfolgende Simulation.
• Dies wiederholen wir iterativ, bis gerade keine mehrfachen Prellungen (Kontakt-Status=0,5) mehr auftreten:

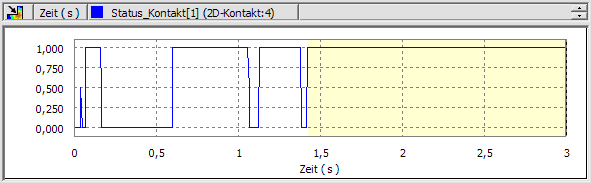
• Dadurch verändert sich das simulierte Bewegungsverhalten, wie man an den veränderten Kontaktzeiten zwischen Unruhe-Ellipse und Anker-Gabel erkennt. Im Beispiel ergibt sich jedoch abschließend wieder ein Verklemmen der Mechanik, was auf eine reale Eigenschaft dieses Systems hindeutet.
• Die Simulationsgeschwindigkeit erhöht sich durch die Vergrößerung der Erfassungsgeschwindigkeit meist beträchtlich, weil die zeitaufwändige Ereignisbehandlung der Prellvorgänge entfällt.

Frage 1: Wie groß ist die ermittelte Erfassungsgeschwindigkeit, bei der im jetzigen Zustand der Modell-Inbetriebnahme gerade keine mehrfachen Prellungen in der Ankergabel mehr auftreten? Das zugehörige Ausgabediagramm ist als Datei Uhrwerk_xx_A.iaa zu speichern (xx=Teilnehmer-Nr. 00..99). .iaa-Dateien enthalten die kompletten simulierten Signalläufe!

Hinweise:

• Die Erfassungsgeschwindigkeit darf auf keinen Fall zu groß gewählt werden, weil ansonsten die real vorhandenen Prellvorgänge an den Kontakten nicht mehr nachgebildet werden können!
• In den folgenden Schritten der Inbetriebnahme des Modells kann es erforderlich sein, die Erfassungsgeschwindigkeit nachzustellen. Die eingesendete Modelldatei soll (unabhängig von Antwort 1) die abschließend als optimal empfundenen Simulationseinstellungen enthalten.

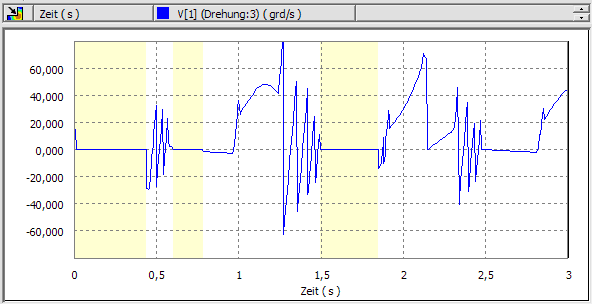
Interessant ist nun der Einfluss dieser Änderung auf das simulierte Verhalten. Mit der Standardeinstellung der Erfassungsgeschwindigkeit sind die vielen Prellvorgänge in den Signalverläufen der Kontaktgeschwindigkeiten deutlich sichtbar:

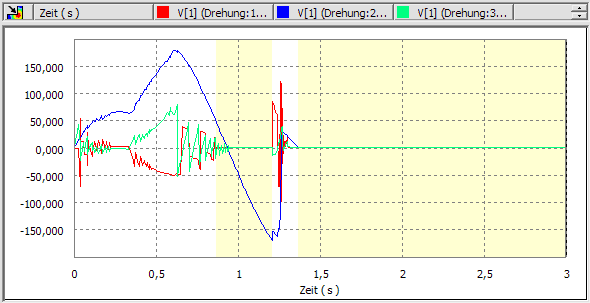
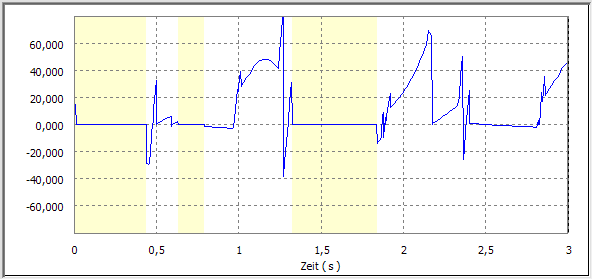
Im Vergleich dazu kommt es bei der "entprellten" Simulation zu wesentlich stetigeren Verläufen der Kontaktgeschwindigkeiten:

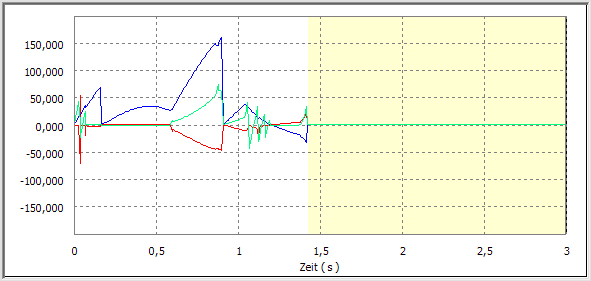
Je nach gewählter Erfassungsgeschwindigkeit kann sich das simulierte Verhalten infolge der Auswirkung der Prellvorgänge merklich ändern. Insgesamt erscheint der "geglättete" Bewegungsverlauf glaubwürdiger als die Vielzahl von überlagerten Mikroschwingungen.

Anpassung von Modellparametern

Wir können feststellen, dass trotz einer günstigeren Konfiguration der numerischen Integration weiterhin ein stochastisches Verhalten des Modells beobachtet werden kann. Dieses resultiert aus dem Zusammenwirken der Vielzahl von Prellvorgängen. Je nachdem, an welcher Position ein Bauteil vom nächsten Stoß "überrascht" wird, sorgt es selbst für "Überraschungen" durch ein verändertes Bewegungsverhalten. Das im Beispiel beobachtete Verklemmen des Mechanismus tritt also "irgendwann" nach nicht vorhersagbarer Zeit auf!

Im nächsten Schritt bemühen wir uns um eine Anpassung der Modellparameter an den realen Kontaktstellen beobachtbare Verhalten:

• Als Kontaktparameter haben wir bisher die idealisierten Parameter der vorgegebenen Werkstoffpaarungen benutzt (Stahl auf Stahl mit Stoßkoeffizient 0,8 und einem Reibkoeffizienten 0,15).
• Das führt beim Kontakt starrer Körper (z.B. Stahlkugel auf dicker Stahlplatte) sicher zu plausiblem Verhalten.
• Vergleichen wir die Anzahl der Prellvorgänge zwischen Simulation und realem Verhalten, so findet man in dem realem Aufbau bedeutend weniger Prellungen (fast keine, wie man in der Flash-Animation sieht):
  

  Schweizer Hemmung
  Flash-Animation

Ursache dieses unterschiedlichen Prellverhaltens sind:

1. Modellvereinfachung durch nicht berücksichtigte Lagerreibung, die dämpfend wirkt.
2. Verformung von Bauteilen in der Realität, die infolge innerer Dämpfung Stoßenergie vernichtet. Im Modell sind alle Bauteile ideal starr!

Im Beispiel wurde das Sicherungselement in der Ankergabel nicht mit modelliert, welches unzulässige Prell-Amplituden zwischen Anker-Gabel und den Anker-Anschlägen verhindert:

• Im Rahmen der Übung wollen wir den Aufwand für dieses zusätzliche Bauteil einsparen.
• Wir konfigurieren die Kontakstellen zwischen Anker-Gabel und den beiden Anschlägen als ideal plastischen Stoß (Stoßzahl=0). Da es nun kein Prellen des Ankers an diesen Anschlägen mehr gibt, sollte man ein plausibleres Modellverhalten erwarten, weil diese Störungen entfallen.

Als besonders kritisch erweisen sich die vielen Prellungen der Unruhe-Ellipse in der Ankergabel:

• In der Realität treten diese Prellungen anscheinend kaum auf!
• Wir setzen deshalb in dieser Kontaktstelle ebenfalls Stoßzahl=0.

Als nächstes widmen wir uns den Prellungen zwischen den Anker-Paletten und dem Hemmungsrad:

• In der obigen Flash-Animation erkennt man aufgrund der schlechten Bildqualität praktisch kein Zurückprellen des Hemmungsrades, wenn es auf eine Ankerpalette schlägt.
• In der Realität sieht man bei genauem Hinschauen höchsten einen kleinen Prellvorgang.
• Im Modell werden wir die Kontaktparameter so einstellen, dass nur eine kleine Prellung in der Simulation erkennbar ist.
• Dazu müssen wir zuvor eine Ausgangsstellung erzeugen, von der ausgehend während der Simulation beide Ankerpaletten nacheinander mit dem Hemmungsrad kollidieren!

Falls man solch eine Ausgangsstellung nicht findet, weil ständig das Hemmungsrad unter die Palette rutscht, anstatt dort nur anzuschlagen:

• Dann hilft nur ein Justage-Vorgang für die Paletten, den der Uhrmacher bei der Uhrenmontage ebenfalls vornimmt.
• Diese Änderungen kann man innerhalb der Umgebung der Dynamischen Simulation im Konstruktionsmodus vornehmen (Ankerbaugruppe > Kontextmenü > Bearbeiten, danach )
• Die Paletten dürfen danach jedoch nur soweit herausragen, dass nach dem Umklappen des Ankers mittels der Unruhe-Ellipse eine sichere Auslösung erfolgen kann.
• Es ist eine Ausgangsstellung zu konfigurieren, mit welcher die erforderlichen Kollisionen zwischen den beiden Ankerpaletten und dem Hemmungsrad simuliert werden können.

Frage 2: Um welchen Betrag muss man die Anker-Paletten für eine sichere Funktion nach außen verschieben? Die endgültige Konfiguration des Modells ist zu speichern. Das zugehörige Ausgabediagramm ist als Datei Uhrwerk_xx_B.iaa zu speichern (xx=Teilnehmer-Nr. 00..99).

Das folgende Diagramm zeigt den Signalverlauf der Drehgeschwindigkeit des Hemmungsrades. Deutlich sind die mehrfachen Prellvorgänge an den Ankerpaletten erkennbar:

Durch Verringerung der Stoßzahl in den zugehörigen Kontakten gelingt die Reduktion auf eine Prellung pro Kollision:

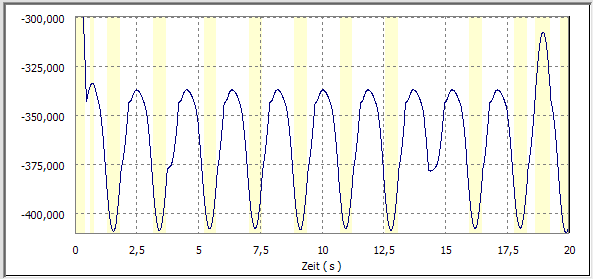
Ziel ist ein nachhaltiges, gleichmäßiges Schwingen der Unruhe. Dieses kann man anhand der Winkel-Position der Unruhe beurteilen. Hierfür sollen je nach Leistungsfähigkeit des PC in dieser Übung 8 s genügen:

Frage 3: Auf welchen Wert muss man die Stoßzahlen in den Kontakten zwischen Hemmungsrad und Ankerpalette verringern, dass maximal eine kleine Prellung übrig bleibt und das System nachhaltig schwingt? Das zugehörige Ausgabediagramm mit einer Simulationszeit von 8 s ist als Datei Uhrwerk_xx_C.iaa zu speichern (xx=Teilnehmer-Nr. 00..99).

← →