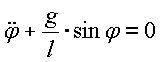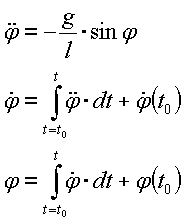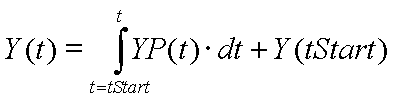Grundlagen: Simulation - Solver

Modellberechnung

Simulationen mit numerischen Modellen beruhen im Wesentlichen auf der Berechnung von Modell-Ergebnissen mit Hilfe eines Gleichungslösers (Solver). In diesem Grundlagen-Kapitel liegt der Schwerpunkt auf der Erläuterung der prinzipiellen Wirkungsweise von Solvern zur Simulation dynamischer Systeme im Zeitbereich. Dabei wird beispielhaft Bezug genommen auf die Begriffe und Konzepte, wie sie im Simulationssystem SimulationX verwendet werden.

Numerische Simulation zeitkontinuierlicher Systeme

Kenngrößen eines Simulationslaufes (Zeitachse)

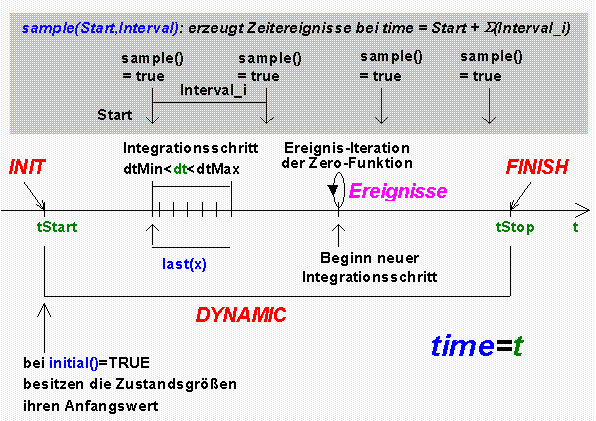
• Aus Sicht des Modells läuft die Simulationszeit time bzw. t in diskreten Schritten dt von tStart bis tStop (meist vorwärts):
  
• Innerhalb des aktuellen Zeitintervalls dt werden in Abhängigkeit vom verwendeten Lösungsverfahren mehrere Stützstellen berechnet:
  • Jede Stützstelle entspricht einer einmaligen Modellberechnung. Demzufolge sind die meisten Modelldurchrechnungen Hilfsrechnungen (mit "unexakten" Werten).
  • Nach Durchführung aller Hilfsrechnungen erfolgt einmalig für das Ende des aktuellen Zeitintervalls dt eine Modellberechnung mit den "richtigen" Modellwerten.
  • Innerhalb des Modell-Algorithmus kann man auf die letzten "richtigen" Modellwerte zugreifen (in SimulationX mit der last-Funktion).
• Bei numerischen Verfahren mit Schrittweitenregelung erfolgt eine automatische Anpassung der Schrittweite dt an die Eigenschaften des Modells zum berechneten Zeitpunkt ("Wie schnell können sich die physikalischen Zustandsgrößen ändern?"):
  • Je empfindlicher Zustandsgrößen des Modells auf andere Modellgrößen reagieren können, desto kleiner wird dt gewählt.
  • Die zulässige Rechenschritte dt kann man begrenzen (dtMin soll "ewiges" Rechnen vermeiden / dtMax soll eckige Signalverläufe vermeiden).
• Die Berechnung mit der sich kontinuierlich anpassenden Schrittweite dt wird gestört durch Ereignis-Zeitpunkte, welche "exakt" angesteuert und berechnet werden müssen. Die Wirkungsweise der erforderliche Ereignisbehandlung wird in einem gesonderten Abschnitt erläutert.

Abschnitte eines Simulationslaufes

Ein Simulationslauf im Zeitintervall tStart ≤ time ≤ tStop besteht aus den Abschnitten INIT, DYNAMIC und FINISH. Im Folgenden wird die Aufgabe dieser Abschnitte zum einen aus numerischer Sicht erläutert. Zum anderen erfolgen Hinweise, welche Aufgaben die zugehörigen Modellabschnitte für die Nutzung von Modellen im Konstruktionsprozess übernehmen:

INIT ( time = tStart )
dient der Ermittlung konsistenter Anfangswerte für alle Zustandsgrößen (Bilder aus der SimulationX-Hilfe):

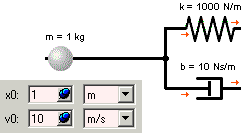
• Die Anfangswerte charakterisieren den (energetischen) Zustand des Modells zu Beginn der Simulation.
• Anfangswerte gewöhnlicher DGL sind immer konsistent (ODE: Ordinary Differential Equation). Der Solver kann daraus eindeutig die Werte der höchsten Ableitungen berechnen (im Beispiel Beschleunigung a(tStart)=-1100 m/s²).
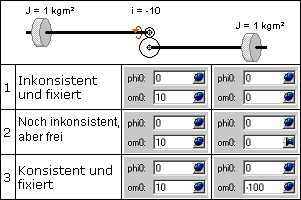
• Modelle mit Zwangsbedingungen (z.B. für Getriebe) führen zu Algebro-Differenzialgleichungen (DAE: Differential Algebraic Equation). Hier können einige Zustandsgrößen nicht unabhängig voneinander gewählt werden:
  
• Man muss sich entscheiden, welche Anfangswerte man definiert vorgibt (fixiert). Die nicht fixierten Anfangswerte versucht der Solver, aus den im Modell in Form von Gleichungen beschriebenen Zwangsbedingungen zu berechnen. Dies gelingt insbesondere bei stark nichtlinearen oder nicht nichteindeutigen Zusammenhängen nicht immer!
• Man sollte möglichst viele gültige Anfangswerte vorgeben und fixieren! Nur dort, wo die analytische Berücksichtigung der Abhängigkeiten praktisch unmöglich ist, überlässt man dem Solver die Anfangswertbestimmung!

Idealisierte Netzwerkelemente besitzen konzentrierte Parameter (Punktmasse, Elastizität, Widerstand usw.):

• Über die Dimensionierungsgleichungen der Elemente ist eine Transformation konstruktiver Kenngrößen (Geometrie und Stoffeigenschaften) in die erforderliche konzentrierten Parameter möglich.
• Für die zeitunabhängigen konzentrierten Parameter sollte diese Dimensionierungsgleichungen in den INIT-Abschnitt der Modell implementiert werden. Es entstehen dadurch Modell-Elemente, welche mit konstruktiven (stofflich-geometrischen) Parametern gespeist werden (Abmessung, Dichte, E-Modul usw.).

DYNAMIC ( tStart ≤ time ≤ tStop )
Es wirkt die Überführungsfunktion des dynamischen Systems (DGL=dynamisches Modell):

• Die numerische Lösung des DGL-Systems berechnet die zeitliche Entwicklung aller Zustandsgrößen in Form von Signalverläufen.
• Alle Modellgrößen, deren Werte von den Zustandsgrößen abhängig sind, werden ebenfalls als Signalverläufe berechnet.
• Die mit dem Modell berechneten Signalverläufe repräsentieren das zeitliche Verhalten des abgebildeten Originals.

FINISH ( time = tStop )
ermöglicht die abschließende Berechnung integraler Werte (z.B. mittlere Verlustleistung, Statistik, Fourieranalyse):

• Im FINISH-Abschnitt des Modells sollte die automatisierte Auswertung der im DYNAMIC-Abschnitt berechneten Signalverläufe implementiert werden.
• Wichtig für die weitere Verwertung der Simulationsergebnisse im Konstruktionsprozess sind Bewertungsgrößen, welche die Qualität des Modellverhaltens repräsentieren (z.B. Wirkungsgrad oder Kosten aus Material- und Energieverbrauch). Möglich wäre hier auch eine "ästhetische" Bewertung im Sinne der Eleganz des Bewegungsablaufs in einem Antrieb.

Ableitungs- und Integralform von DGL

Die Überführungsfunktion eines dynamischen Modells stellt ein DGL-System dar. Zur Lösung dieses DGL-Systems verwenden die Solver Verfahren der numerischen Integration:

• Zweck der Verfahren zur numerischen Integration ist die näherungsweise Berechnung der Fläche (bestimmtes Integral) unter einem Funktionsverlauf (Ableitung).
• Es existieren zwei grundsätzliche Möglichkeiten, um ein DGL-System zu notieren (hier am Beispiel des Pendels):
  1. Ableitungsform:
     
  2. Integralform:
     
• Die Integralform enthält explizit die Zustandsgrößen als Ergebnis einer numerischen Integration. Insofern ist diese Form für den technischen Anwender meist anschaulicher als die Ableitungsform.
• Unabhängig von der im Modell gewählten Notation erfolgt durch das Simulationssystem für den Anwender unsichtbar eine Transformation in die für den Solver geeignete Form eines DGL-Systems.

Wechselwirkung von Zustandsgroesse Y und Ableitung YP

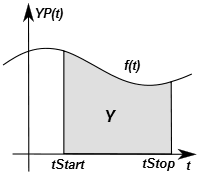
Y(t) als Resultat einer Integral-Bildung kann geometrisch als Fläche unter dem Funktionsverlauf der zugehörigen Ableitung YP(t) interpretiert werden:

• Y(t) repräsentiert in einem dynamischen Modell die Füllung eines Speicher-Elements mit Energie, Stoff bzw. Information (=Zustandsgröße). YP(t) ist dabei die Änderungsgeschwindigkeit dY/dt für die Füllung des Speicherelements.
• Im Allgemeinen ist YP(t)=f(Y(t)), d.h. die Geschwindigkeit des Energie- /Stoff- /Info- Flusses zwischen den Speichern ist abhängig von den Potentialdifferenzen und den Übertragungselementen zwischen den Speichern.
• Da YP(t) somit nicht explizit gegeben ist, kann Y(t) nicht hinreichend genau durch numerische Verfahren der Flächenberechnung ermittelt werden (z.B.: Trapez- /Tangentenformel oder Simpsonsche Regel).
• Die konkreten zeitlichen Verläufe von Y(t) und YP(t) ergeben sich erst durch die zeitliche Wechselwirkung zwischen den Energiespeichern!

Zentraler Integrationskern (Solver)

Es existieren verschiedene Verfahren zur Lösung (=Simulation) von DGL mittels numerischer Integration. Diese Verfahren sind meist in einem "zentralen Integrationskern" = "Solver" implementiert:

• Die Integral- bzw. Differential-Funktion ist die Grundlage für die Verbindung zwischen Modell und Solver:

:
a  := F/(m);
v  := integral (a,v0);
x  := integral (v,x0);

• Es sieht auf den ersten Blick so aus, als würde über diese Funktionsaufrufe der zentrale Integrationskern vom Modell aus aufgerufen, jedoch verhält es sich umgekehrt!
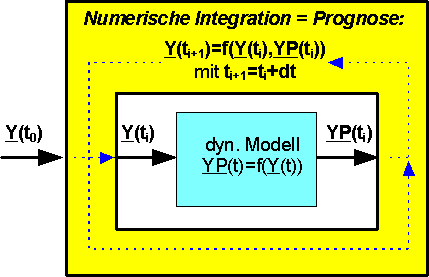
• Das Modell ist aus Sicht der numerischen Integration eine Black-Box, welche die Ableitungen der Zustandsgrößen berechnet:
  

Prinzip der numerischen Integration

Das DGL-System wird durch die numerische Integration zum "Leben" erweckt. Es entwickelt eine Eigendynamik auf der Basis seiner Elemente (Speicher, Übertragungsglieder und Wandler) und ihrer Wechselwirkung. Der Solver ist in der Lage, über einen begrenzten zeitlichen Prognosehorizont den Zustand des Systems hinreichend genau vorauszusagen:

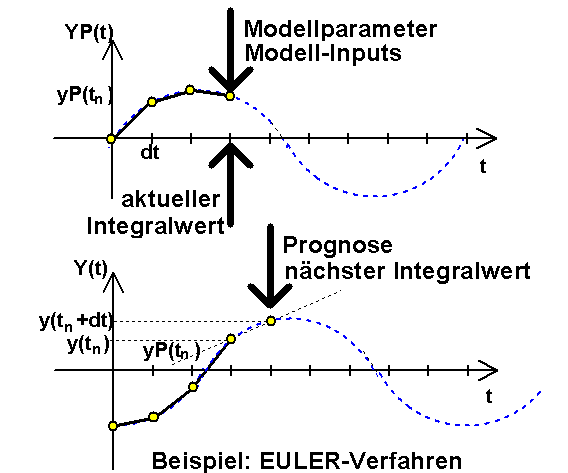
• Ausgehend von den Werten der Zustandsgrößen und Eingangssignale zum aktuellen Zeitpunkt t_n sowie den Modellparametern werden mit dem Modell die zeitlichen Ableitungen YP(t) der Zustandsgrößen Y(t) ermittelt.
• Mit dieser "Abschätzung" der zeitlichen Änderung der Zustandsgrößen prognostiziert der Solver über das Zeitintervall dt die Werte der Zustandsgrößen für den Zeitpunkt t_n+dt.
• Im obigen Bild wird dies am Beispiel des EULER-Verfahrens verdeutlicht. Bei diesem Verfahren wird vereinfachend angenommen, dass die Ableitung der Zustandsgrößen im Zeitintervall dt konstant auf dem Wert YP(t) bleibt.
• Nach der Art und Weise, wie die Prognose der Zustandsgrößen für den nächsten Integrationsschritt dt erfolgt, kann man die Verfahren der numerischen Integration grob in grundsätzliche Klassen einteilen. Diese Klassifizierung der Integrationsverfahren soll in den folgenden Abschnitten kurz vorgestellt werden.

Explizite und implizite Verfahren

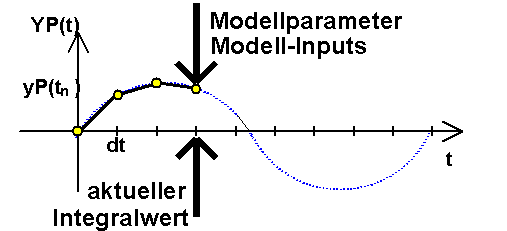
Zum aktuellen Zeitpunkt t_n werden mit dem dynamischen Modell die aktuellen zeitlichen Ableitungen der Zustandsgrößen berechnet:

• Der effektive Wert der Ableitung der Zustandsgrößen gemittelt über das gesamte Intervall dt wird unabhängig von der Einteilung in explizit/implizit durch Hinzunahme weiterer Informationen "geschätzt".
• Die Prinzipien dieser Abschätzung werden in den folgenden Abschnitten noch erläutert.

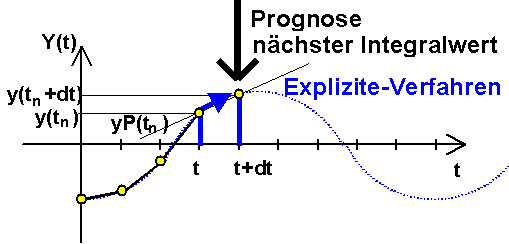
Explizite Verfahren betrachten den Schätzwert für die effektive Ableitung YP als hinreichend genau. Grafisch stellt sich die Prognose einer Zustandsgröße für den Zeitpunkt t_n+dt als Anstieg der Tangente YP an die Zustandsgröße YP(t_n) im Intervall dt dar:

• Der prognostizierte Wert der Zustandsgrößen wird ebenfalls als hinreichend angenommen und ist Ausgangspunkt für die Berechnung des nächsten Zeitschrittes dt.

Implizite Verfahren bewegen sich im Zeitbereich nicht so geradlinig vorwärts wie explizite Verfahren. Die Berechnung jedes Zeitschrittes dt ist durch eine Iterationsschleife gekennzeichnet:

===>>> Dieses Kapitel wird zur Zeit erarbeitet !!! <<<===

Vorläufige weitere Gliederung:

• Einschritt- und Mehrschritt-Verfahren
• Explizite Einschrittverfahren (Beispiele)
• Implizite Verfahren (Prinzip)
• Implizite Verfahren (Prädiktor-Korrektor-Verfahren)
• Qualitäten von Integrationsverfahren
• Konfiguration des Solvers

Zeitdiskrete Ereignisse

• Ereignisse im Simulationslauf
• Numerische Definition von Ereignissen
• Klassifizierung numerischer Ereignisse
• Ereignisbehandlung (SimulationX)
• Beispiel: Extremwert-"Sensoren" (SimulationX)

Lineare und nichtlineare Systeme

• Modellcharakter von Systemen
• Dynamische Systeme
• Wann kann man ein System als Linear behandeln?
• Wann muss man ein System als Nichtlinear behandeln?