Software: SimX - Magnetoptimierung - Ersatzmodell-Identifikation

↑

← →

Ersatzmodell-Identifikation

Im OptiY werden wir nun den Experimentworkflow an das veränderte FE-Modell und an das veränderte Input-File anpassen:

• Wir definieren einen zusätzlichen Nennwert dAnker in [mm] als Konstante mit dem bisherigen Wert 10.
• Wir öffnen das Input-File Eingabe.txt erneut und knüpfen wegen der veränderten Parameter-Positionen alle Verbindungen neu (incl. dAnker).
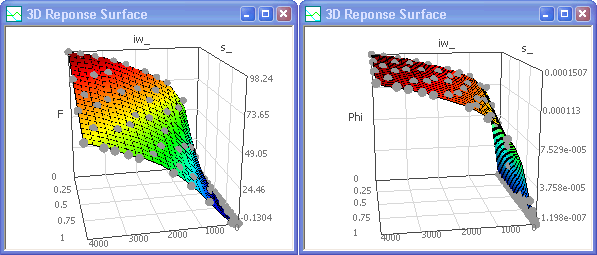
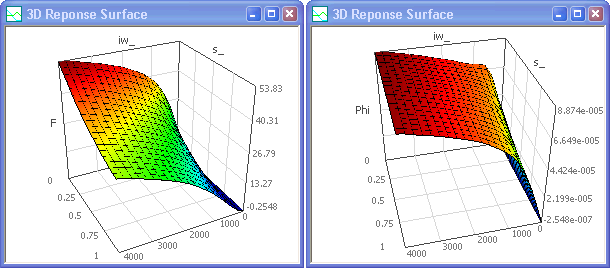
• Die erneute Kennfeld-Identifikation mit den Variablen iw und s ergibt leicht veränderte Funktionswerte, da der Magnet leicht veränderte Abmessungen besitzt:
  

Nun kommt der entscheidende Schritt zu einem Ersatzmodell mit konstruktiven Basis-Variablen:

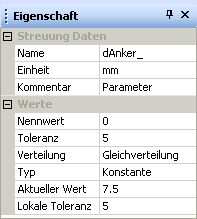
• Wir ergänzen die Streuung dAnker_ mit einem Streubereich von 5...10 mm:
  
• Wir führen wieder mit Full Factorial nichtadaptivem Design (Versuchsplannung) mittels Gauss-Prozess eine Identifikation der Antwortflächen durch:

F   ... Exponential       mit Polynomordnung=2 
Phi ... Gamma Exponential mit Polynomordnung=2

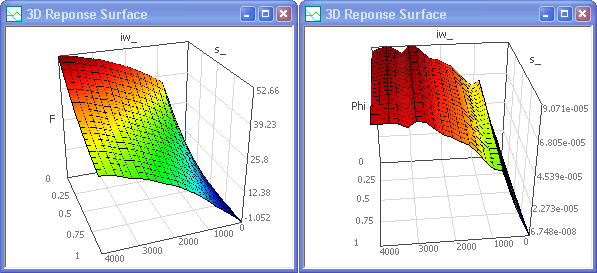
• Hinweis: Da die zuletzt verwendete Stufung=4 für das Full Factorial Design etwas grob war, sollte eine feinere Stufung verwendet werden. Eine Stufung=5 würde 5x5x5=125 Modellaufrufe erfordern. Leider kommt es mit diesem Raster beim Gauss-Prozess zu einer Fehlermeldung "No inverse Matrix". In diesem Fall half nur ein Wechsel der Stufung, im Beispiel auf Stufung=6 mit 6x6x6=216 Modellaufrufen:
  

Man könnte ausgehend von diesem Raster den adaptiven Gauss-Prozess starten, da das Phi-Kennfeld noch sehr wellig ist und das Kraftfeld eine negative Kraft von ca. -1 N bei einer Durchflutung=0 A erzeugt:

• Leider führt das nur teilweise zum Erfolg, indem der Betrag der negativen Kraftwirkung verringert wird.
• Die Welligkeit des Phi-Feldes wird eher stärker und lässt sich auch durch die nachträgliche Wahl anderer Covarianz-Funktionen und Polynomordnungen nicht im erforderlichen Maße verrringern.
• Vermutung: Das gleichmäßige Raster des Factorial Design ist sehr ungünstig für den Gauss-Prozess, da die Periodizität der Stützstellen die Ausbildung von Wellen auf der Antwortfläche fördert.

Deshalb wurde für die globale Abtastung im Folgenden die Sampling Methode (Stichprobenumfang=100) mit Gleichverteilung aller Streugrößen benutzt:

• Das vorherige Factorial Design wurde vor allem unter dem Aspekt verwendet, weil damit eine Abtastung der Bereichsgrenzen gewährleistet ist. Damit sollte eine Extrapolation des Ersatzmodells über die Abtastpunkte hinaus vermieden werden.
• Um einen ähnlichen Effekt für die Sample Methode zu erreichen, wird das Latin Hypercube benutzt. Damit wird die Verteilung der Streugrößen auch bei kleinen Streugrößen gleichmäßiger erfasst. Es kann sein, dass es sich hierbei wieder um einen Irrtum handelt und der totale Zufall des Monte Carlo Verfahrens bessere Ersatzmodell liefert!
• Wir wählen trotzdem vorerst das Latin Hypercube Verfahren, um zufällige "riesige" Lücken bei der Abtastung zu vermeiden.

Das Adaptive Design schalten wir anfänglich wieder ab, um die Qualität der Ausgangslösung zu begutachten:

• Mit dem Stichprobenumfang=100 erzielt man mit der Sample-Methode qualitativ ähnliche Antwortflächen wie mit dem Full Factory Design mit einer reichlich doppelt so großen Stichprobe.
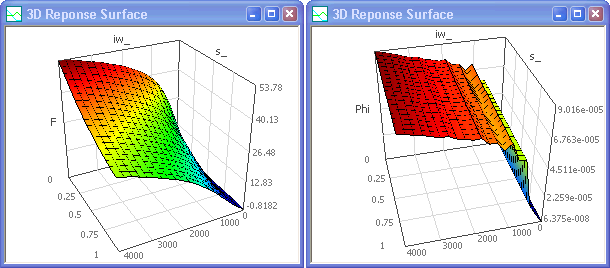
• Nach dem Aktivieren des Adaptiven Designs für den Gauss-Prozess erhält man mit insgesamt ca. 200 Stützstellen im Beispiel eine bedeutende Qualitätsverbesserung insbesondere für die Phi-Antwortfläche:

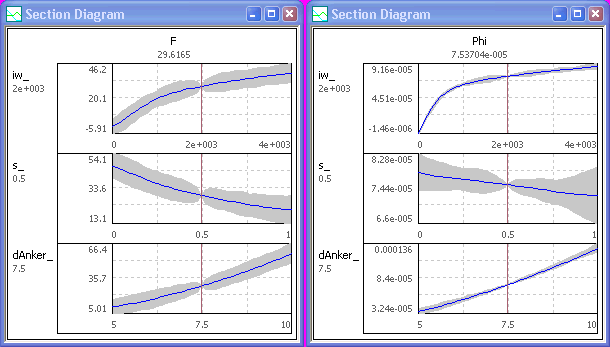
• Die 3D-Antwortflächen sind für den betrachteten 4-dimensionalen Fall ebenfalls Schnittdarstellungen. Welche 3D-Fläche dargestellt wird, hängt vom aktuellen Wert des dritten Parameters dAnker_ ab:

• Dessen Wert (im Beispiel 7.5 mm) wird in den 2D-Schnittdiagrammen als Linie eingeblendet und kann über das Eigenschaftsfeld der Streugröße geändert werden:

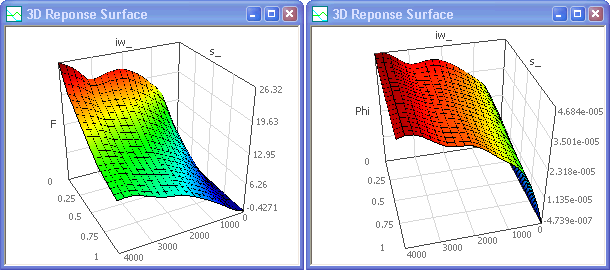
• Ändert man den aktuellen Wert der Streugröße dAnker_, so werden jeweils die zugehörigen 3D-Kennfelder dargestellt. Am welligsten sind die Kennfelder für einen Ankerdurchmesser von 5 mm:

===>>> Hier geht es bald weiter !!!

← →