Software: FEMM - Elektrostatik - Loads und Constraints

<<~ ~>>

^

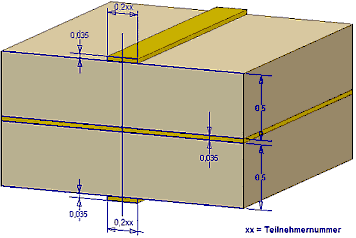
Mittels des FEM-Modells wird das elektrostatische Feld in einem abgegrenzten, mit Isolator-Material belegtem Raum-Bereich berechnet:

• Berechnet werden nur die Potentiale (Spannungen) in den Knoten des endlichen Netzes.
• Die Potentiale in den Knoten sind abhängig von:
  • den Material-Eigenschaften im unendlichen Raum.
  • der Verteilung von Ladungsmengen im unendlichen Raum.
  • vorgegebenen Potentialwerten in ausgewählten Raumbereichen.

Die Material-Eigenschaften des abgegrenzten Raumbereiches haben wir bereits in Form der Dielektrizitätskonstante beschrieben (Luft und Laminat).

Ladungen repräsentieren die Loads in der elektrostatischen Domäne. Für die Definition von Ladungen als Ursache des elektrostatischen Feldes stellt FEMM für alle Property-Klassen entsprechende Möglichkeiten bereit:

• für Material als Raum-Ladungsdichte [C/m³]
• für allgemeine Grenzflächen zur Umgebung (Boundary) als Flächen-Ladungsdichte [C/m²]
• für Knoten (Points) als Linien-Ladungsdichte [C/m]
• Hinweis: Knoten beschreiben:
  • im planaren Fall Strecken (entlang der "Dicke")
  • im axialsymmetrischen Fall Kreise (mit Radius um Y-Achse)!
• für Grenzflächen zu einem Leiter (Conductor) als Gesamtladung der in sich zusammenhängenden Leiterfläche [C].

Potentiale repräsentieren die Constraints in der elektrostatischen Domäne. FEMM bietet die Möglichkeit, für obige Objekte (außer für Material) Potentiale als Zwangsbedingungen zu definieren:

• Die Potentialvorgabe ist jeweils nur alternativ zur Ladungsdefinition möglich, um damit eine Überbestimmung des Gleichungssystems zu vermeiden.
• Die Potentialverteilung an den Rändern zum "unendlichen" Raum definiert man über so genannte Boundary Conditions. Das sind Gleichungen, welche den Verlauf der Feldlinien an den Rändern beschreiben (z.B. senkrecht oder asymptotisch zum Rand).
• Die Menge aller Potentialvorgaben dient als Randbedingung für das aus dem FE-Netz generierte Differentialgleichungssystem.
  

Mit den bereitgestellten Möglichkeiten kann der Nutzer ausgehend von seiner konkreten Problemstellung sehr direkt die Loads & Constraints für das FE-Modell definieren:

• Im Beispiel des Kondensators ist es sicher sinnvoll, 1 Volt Potentialdifferenz zwischen den beiden Leitungselektroden vorzugeben.
• FEMM berechnet die Ladungen auf den Leitern, wenn man sie nicht vorgibt. Damit entspricht der Zahlenwert der Ladungsmenge [As] auf dem Leiter dem Wert der Kapazität [F], da C=Q/U.
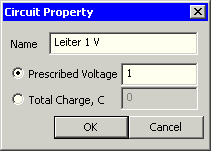
• Definition der Leitungspotentiale (Properties - Conductors - Add Property):
  • Leiter-Potential 1 V
    
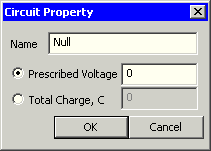
  • Null-Potential für Masse-Ebene
• Diese Leitungspotentiale weisen wir den entsprechenden Randsegmenten der Geometrie zu:
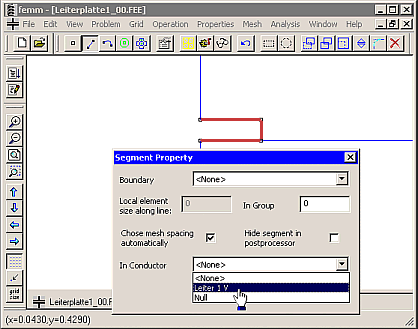
  • Wir markieren mit der rechten Maustaste alle Randsegmente der Leitererbahn und öffnen dann mittels <Leertaste> den Eigenschaftsdialog. Analog ist die Vorgehensweise für das Null-Potential auf dem Masse-Segment:

Hinweise:

• Man hätte die Leitersegmente auch mit einer Boundary Condition mit vorgegebener Spannung belegen können. Daraus würde der gleiche Feldverlauf berechnet. Der Vorteil der Verwendung der Conductor Property ist, dass für jeden Leiter vom FEMM-Solver automatisch die Ladung berechnet wird!
• Für Geometrie-Segmente, für die man keine Boundary Condition oder Conductur Property definiert, wird angenommen, dass die Feldlinien senkrecht auf den Rand treffen. Dies ist z.B. im Sinne der Symmetrie an der Y-Achse auch erforderlich!
• Den "unendlichen" Raum betrachten wir vorläufig noch nicht. Wir gehen davon aus, dass unser Luftraum den wesentlichen Teil des elektrostatischen Feldes erfasst.

<<~ ~>>