Grundlagen: Generatives Design und Strukturoptimierung

Autor: Dr.-Ing. Alfred Kamusella

===>>> Hier entsteht zur Zeit ein neues Grundlagen-Kapitel! <<<===

Strukturoptimierung

Begriffswelt

Umgangssprachlich werden die für die Produkt-Optimierung relevanten Begriffe nicht immer ganz "sauber" verwendet. Dies kann dann dann durchaus zu Missverständnissen in der fachlichen Kommunikation führen. Deshalb soll im Folgenden eine Einordnung der wesentlichen Begriffe in Hinblick auf die Optimierung mechanischer Strukturen vorgenommen werden:

"Struktur" ist ein ziemlich abstrakter Begriff aus der Systemtheorie:

• Ein beliebiges System wird beschrieben durch die Abgrenzung und die Schnittstellen zu seiner Umgebung sowie durch seine innere Struktur.
• Die (innere) Struktur eines Systems ist definiert durch die Summe aller System-Elemente und ihrer Interaktion.

"Strukturoptimierung" im hier behandelten Sinne bezieht sich nur auf mechanische Strukturen:

• Optimiert werden z.B. mechanische Bauteile, welche durch Modelle der Strukturmechanik berechnet werden können. Die Einbeziehung zusätzlicher physikalischer Domänen ist dabei möglich (z.B. Wärme, elektromagnetische Felder).
• Die angewandten Begriffe, Vorgehensweisen und Verfahren sind im Prinzip aber auch auf beliebige "Strukturen" zumindest sinngemäß übertragbar.
• "Strukturoptimierung" ist der Oberbegriff für die Optimierung grundlegender Struktur-Eigenschaften:

1. Topologie
2. Form (Gestalt)
3. Abmessung (Dimensionierung)
4. Material

Topologie

Bezogen auf strukturmechanische Systeme beschreibt die Topologie diejenigen geometrischen Eigenschaften von Körpern, die bei zulässigen stetigen Verformungen erhalten bleiben:

• Z.B. besitzen eine Tasse und ein Volltorus die gleiche Topologie, sie sind zueinander homöomorph. D.h., beide Körper sind umkehrbar eindeutig stetig aufeinander abbildbar und aus der Sicht der Topologie deshalb nicht zu unterscheiden (Bild aus Wikimedia-Commons).
• Vereinfacht kann man sich als mathematischer Laie merken, dass zwei Körper die gleiche Topologie besitzen, wenn sie über die gleiche Anzahl durchgängiger Löcher und in sich abgeschlossener Hohlräume verfügen. Damit besitzen eine Kugel und ein Würfel die gleiche Topologie wie ein Trinkbecher, aber nicht die gleiche Topologie wie die Tasse!
• Anschauliche stetige Verformungen für den Erhalt einer Topologie sind dabei das Dehnen, Stauchen, Verbiegen, Verzerren, Verdrillen und Verkrempeln. Nicht zulässige Verformungen sind das Beseitigen vorhandener Löcher/Hohlräume oder das Schaffen neuer Löcher/Hohlräume.
• Das folgende Bild zeigt zwei unterschiedliche Topologien für ein funktionell identisches Bauteil:
  

Form

Jede mögliche Topologie eines Bauteils kann in unterschiedlichster Form (Gestalt) auftreten:

• Die Vielfalt der möglichen Formen einer Topologie ist begrenzt durch die Menge möglicher zulässiger stetiger Verformungen.
• Man kann unterscheiden in abstrakte und realisierte (konkrete) Formen:
  1. Abstrakte Form
     • wird beschrieben durch geometrische Abhängigkeiten zwischen den Kanten und Flächen als Form-Elementen (z.B. parallel, lotrecht, fluchtend, gleich, symmetrisch) → Analogie: im CAD die Liste aller Skizzier-Abhängigkeiten zur Stabilisierung der gewünschten 2D-Formen;
     • bei [Freiformflächen] erfolgt die Beschreibung überwiegend durch die Topologie des Bauteils mit zusätzlichen Symmetrie-Eigenschaften und Randbedingungen.
  2. Konkrete Form
     • entspricht der geometrischen Realisierung einer (abstrakten) Form unabhängig vom konkreten Material (z.B. in Form eines 3D-Geometriemodells);
     • die konkrete Größe einer Form ist nur beispielhaft und noch nicht durch Maße festgelegt → Analogie: im CAD die unbemaßte Skizze mit durch Skizzier-Abhängigkeiten stabilisierten 2D-Formen.

Abmessung

Erst durch die Festlegung von Positionen, Linienverläufen und Querschnitten durch konkrete Zahlenwerte wird die Geometrie eines Bauteils vollständig bestimmt:

• Die Bestimmung der konkreten Maße für eine konkrete Form erfolgt durch den Prozess der Dimensionierung.
• Grundlage der Dimensionierung ist die quantitative Berücksichtigung der Belastung des Bauteils (mechanisch, thermisch, ...).
• Die Detail-Abmessungen der Form müssen dabei so gewählt werden, dass das Bauteil allen berücksichtigten Belastungen standhält.
• Wichtig: Dimensionierung ist meist abhängig vom zuvor für das Bauteil gewählte Material.
• Im Spezialfall können Abmessungen auch ohne Materialeinfluss direkt durch die Funktion bestimmt sein (z.B. Anlageflächen, Abstände zwischen Gelenken)

Material

Ein Bauteil kann nur mittels Material realisiert werden. Dadurch wirken im Bauteil die konkreten Material-Eigenschaften und es ergeben sich bestimmte Fertigungsrestriktionen:

• Veränderte Festigkeitseigenschaften, aber auch anderer Materialeigenschaften haben meist Auswirkungen auf die Dimensionierung der Abmessungen.
• Veränderte Fertigungsrestriktionen (welche z.B. andere Fertigungsverfahren bedingen) haben Auswirkungen auf mögliche konkrete Formen des Bauteils. Dies kann auch zu einer Nichtrealisierbarkeit bestimmter Topologien führen.
• Veränderte Isotropie-Eigenschaften bedingen andere optimale Topologien und damit auch andere mögliche Formen.

Klassifizierung der Optimierungsverfahren

Es geht in diesem Abschnitt nicht um konkrete Optimierungsalgorithmen und nicht um konkrete Methoden der Zielfunktionsformulierung. Es soll hier nur ein Überblick gegeben werden, wofür numerische Optimierung im Rahmen der Strukturoptimierung genutzt wird, an welchen Strukturparametern "gedreht" werden kann und welche Prinzipien dabei zur Anwendung kommen.

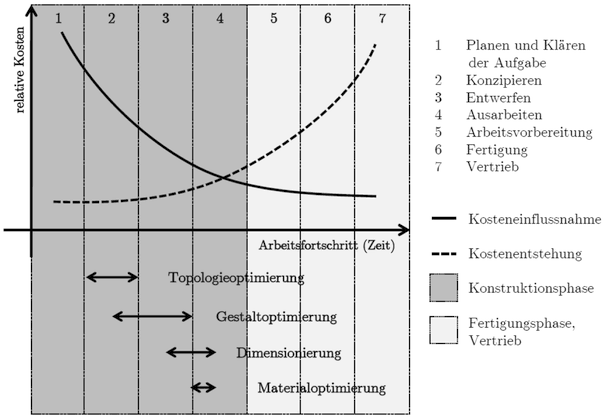
Klassifizierung nach Einsatz im Konstruktionsprozess

Innerhalb des Konstruktionsprozesses werden die einzelnen Aspekte einer Bauteil-Struktur nacheinander in der folgenden Reihenfolge jeweils einer Optimierung unterzogen (Bild aus Arion-Theoriehandbuch):

1. Topologie
2. Form (Gestalt)
3. Abmessungen (Dimensionierung von Querschnitten)
4. Material
   

Für die einzelnen Aspekte können dabei isoliert optimale Lösungen gesucht werden. Meist existieren jedoch Wechselwirkungen zwischen den Struktur-Aspekten, die dann z.B. zu einem iterativen Vorgehen zwingen, wenn die unterschiedlichen Kriterien nicht zu einer gemeinsamen Zielfunktion zusammengeführt werden können:

• Die klassische Optimierung der Abmessungen (Dimensionierung) und des Materials besitzt zwar ein hohes Potential zur Verbesserung der Funktionalität, besitzt aber meist nur geringen Einfluss auf die Kosten im Produktlebenszyklus.
• Die vorgelagerte Topologie- und Formoptimierung mit einem weit höheren Einfluss auf die Produktkosten überlässt man heute meist noch der Kreativität und dem Erfahrungswissen der Entwicklungsingenieure.

Die Optimierung der einzelnen Struktur-Aspekte verfolgt unterschiedliche Ziele. Diese sollen im Folgenden kurz erläutert werden:

Topologie-Optimierung

Ziel der Topologie-Optimierung ist immer die Erfüllung der Anforderungen an ein Bauteil mit möglichst geringem Einsatz von Material:

• Häufig wird dafür z.B. eine maximale Steifigkeit bei niedrigem Volumen angestrebt. Dies ermöglicht effizienteren Materialeinsatz und verbessert die Bewegungsdynamik durch geringere Masse.
• Ausgangspunkt ist der Bauraum, welcher für das betrachtete Bauteil zur Verfügung steht. Dieser wird im Sinne einer Ausgangslösung vollständig mit einem "sinnvollen" Material gefüllt.
• Anzugeben sind alle Stellen, an denen Belastungen auf das Bauteil wirken, sowie die Art der jeweiligen Belastung.
• Bei der "reinen" Topologie-Optimierung wird die Festigkeit des Bauteils meist nicht berücksichtigt, sondern nur für einen minimalen Füllgrad des Bauraums auf eine maximale Steifigkeit hin optimiert. Deshalb ist es erforderlich, anhand von Erfahrungswissen oder einer Grobdimensionierung, ein relatives Zielvolumen (entspricht dem Füllgrad) für das Bauteil vorzugeben (z.B. 40%).
• Es ist außerdem zu definieren, wo die Gestalt nicht verändert werden darf (z.B. Bohrungen zur Lagerung/Befestigung oder Anlageflächen - Beispiel aus Autodesk-Hilfe zu Fusion 365):
  
• Meist existieren Symmetriebedingungen, welche in Form von Symmetrie-Ebenen zu beschreiben sind (z.B. die Mittel-Ebene des obigen Bauteils).

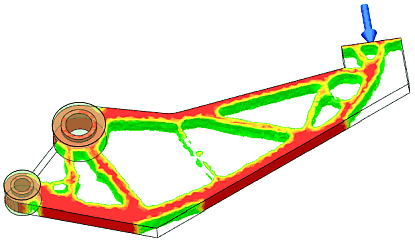
Im Ergebnis der Topologie-Optimierung entsteht eine Tragwerk-ähnliche Struktur im Bauraum außerhalb der fixierten Bereiche. Diese Struktur ist dann in der Lage, mit dem verfügbaren Material einen möglichst gleichmäßigen Kraftfluss zwischen den Belastungsstellen des Bauteils zu realisieren:

• An allen optimierten Stellen des Bauteils erfolgt eine homogene, minimal mögliche Verformung. Die minimale Nachgiebigkeit entspricht einer maximalen Steifigkeit:
  
• Lösungen der "reinen" Topologie-Optimierung kann man meist nur als Design-Vorschlag betrachten. Deutlich wird dies z.B. durch nicht geschlossene "Speichen" bzw. sehr "ausgefranste" Konturen.
• Zumindest ist eine Glättung und Vervollständigung solcher Lösungen erforderlich, bevor man diese weiteren Analysen und Modifikationen unterziehen kann:
  
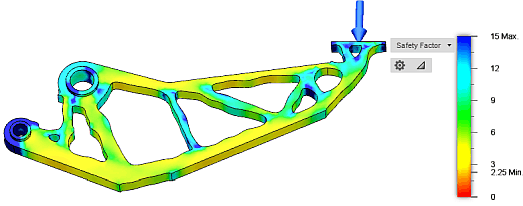
• Die Belastungsanalyse zeigt dann (z.B. anhand des Sicherheitsfaktors), ob nur eine fertigungstechnische bzw. ästhetische Kontur-Nachbearbeitung erforderlich ist oder ob noch prinzipielle Schwachstellen existieren:
  

Form-Optimierung

Formoptimierung (Shape optimal design) bedeutet Modifikation der Oberfläche eines Bauteils mit einem zuvor definierten Optimierungsziel unter Beibehaltung der Bauteil-Topologie:

• Bei der "reinen" Topologie-Optimierung entstehen zwar Bauteile mit hoher Steifigkeit (Stiffness), welche jedoch noch hohe Spannungsspitzen aufweisen können, weil die Homogenisierung der Spannung (Stress) dabei kein Optimierungskriterium darstellt.
• Auch klassisch mittels CAD-Programm entworfene Bauteile besitzen häufig an ihrer Oberfläche Stellen, an denen Kerbspannungen auftreten, welche zu einer verminderten Lebensdauer des Bauteils führen:
  

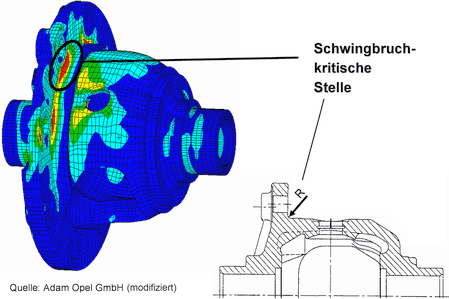
Ziel der Formoptimierung im Rahmen der Strukturoptimierung ist die Minimierung von Spannungsschwankungen im Bauteil:

• Bei der Verformung von Bauteilen treten die höchsten Spannungen an der Bauteiloberfläche auf und dort meist an "Einbuchtungen" in Form der Kerbspannungen.
• Damit beschränken sich die Veränderungen des Bauteils durch die Form-Optimierung automatisch auf die Oberfläche.

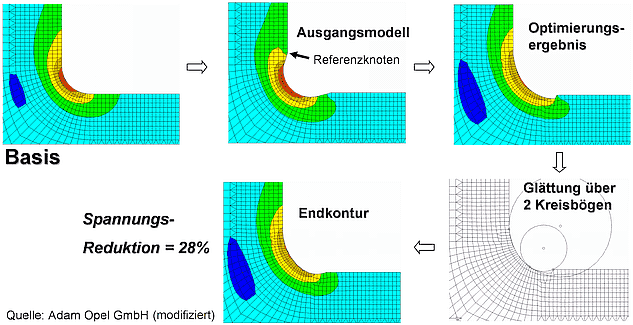
Das folgende Beispiel bezieht sich auf das vorherige Bild einer Ausgangslösung und zeigt die Schritte der Formoptimierung ausgehend von einem Hinterschnitt (Ausgangsmodell) bis zur optimierten Kontur, über die Glättung bis zur optimierten Kontur im schwingbruchkritischen Bereich:

Wichtig:
Bei der "reinen" Form-Optimierung wird die Festigkeit ebenfalls nicht berücksichtigt. Es geht nur um die Minimierung von Potential-Unterschieden, d.h. um die Minimierung von Spannungsspitzen in der Strukturmechanik.

Querschnitt-Optimierung

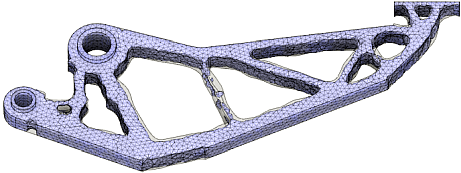
Die vorherigen beiden Stufen der Struktur-Optimierung sorgten nur für eine Volumen-reduzierte Lösung mit maximaler Steifheit und homogenen Spannungsverläufen. Damit die einzelnen "Streben" der Tragwerk-ähnlichen Struktur der Belastung standhalten, müssen unter Umständen noch ihre Querschnitte angepasst werden.

Bei der "reinen" Querschnittsoptimierung (Sizing) werden ausschließlich Querschnittswerte (z.B. Dicke, Höhe, Durchmesser usw.) als Optimierungsvariable verwendet:

1. CAD-basiert stehen diese Abmessungen prinzipiell als veränderbare Parameter zur Verfügung und können mit dem Ziel der Minimierung von Maximalspannungen für die Querschnittsoptimierung genutzt werden.
2. FEM-basiert ergeben sich die einzelnen Querschnitte aus dem FEM-Netz. Die Form-Optimierung hat praktisch bereits die gewünschte Spannungsminimierung vorgenommen. Deshalb zeigt eine unzulässige Spannung in einzelnen Querschnitten, dass mit dem gegebenen Füllfaktor (z.B: von 40 %) keine tragfähige Struktur für das Bauteil generiert werden konnte → der Füllfaktor muss erhöht werden! Der Prozess beginnt wieder mit einer Topologie-Optimierung und kann sich über mehrere Iterationen erstrecken, bis ein geeigneter Füllfaktor für eine tragfähige Bauteil-Struktur ist.

Material-Optimierung

Die bisherigen Stufen der Struktur-Optimierung verwendeten ein anhand von Erfahrungswerten festgelegtes Material. Erst nach der Form-Optimierung kann man feststellen, ob mit diesem vorgegebenem Material eine Lösung realisierbar ist:

1. Ergibt sich trotz iterativer Erhöhung des Füllfaktors keine Lösung mit ausreichender Festigkeit, so muss man ein stabileres Material wählen. Daraus resultieren Auswirkungen auf den möglichen Füllfaktor, welche unter Umständen mehrere Iterationen innerhalb der Struktur-Optimierung erfordern.
2. Handelt es sich beim vorgegebenen Füllfaktor um eine feste Forderung, so erfordert die Wahl eines anderen Materials nur eine Iteration über die Belastungsanalyse innerhalb der Querschnittsoptimierung.

Die Material- und Querschnittsoptimierung sind eng miteinander verknüpft und beenden gemeinsam den Prozess der Struktur-Optimierung.

Klassifizierung nach Art der Optimierungsparameter

Optimierungsverfahren benötigen immer einen Satz von Optimierungsparametern (Designvariablen) für die Modifikation der aktuellen Lösung. Trotzdem unterscheidet man qualitativ zwischen Parameter- und Parameter-freie Optimierung:

Parameter-Optimierung

Auf Geometrie-Modellierung basierende CAD-Bauteilstrukturen werden selbst bei Verwendung von Freiformflächen immer durch eine bestimmte Anzahl von Parametern beschrieben. Die Veränderung dieser Parameter-Werte führt zu einer definierten Veränderung der Bauteil-Struktur:

• Die Parameter eines CAD-Modells können sich auf unterschiedliche Aspekte der Bauteil-Struktur beziehen, woraus sich unterschiedliche Bezeichnungen für die Art der Parameter-Optimierung ergeben:
  1. Diskrete Topologie-Optimierung (z.B. parametrisierte Anzahl von Streben im Tragwerk)
  2. Parametrische Form-Optimierung (z.B. Kontur-Beschreibung durch Spline-Stützstellen oder Approximation mittels Kreissegmenten)
  3. Nennwert-Optimierung (Abmessungen von Querschnitten und Längen)
  4. Material-Optimierung (Material wird immer durch einen Parametersatz beschrieben)

Die Vorzüge von CAD-Modellen hinsichtlich der Modell-Parametrisierung werden für die Stufen der Topologie- und Form-Optimierung meist vom erforderlichen Modellierungsaufwand aufgezehrt! In der Praxis erfolgen deshalb kaum parametrisierte Topologie- und Form-Optimierungen.

Parameterfreie Optimierung

Existiert die aktuelle Bauteil-Struktur nur als FEM-Modell in Form eines 3D-Netzes, so werden die Topologie und Form des Bauteils durch die "stetige" Verteilung von Struktur-bestimmenden Parametern festgelegt, z.B.:

• lokaler E-Modul repräsentiert "Material" (bei normalem Wert) oder "Loch" (bei kleinem Wert)
• lokale Temperatur-Erhöhung repräsentiert Material-Verdickung

Infolge der endlich vielen Finiten Elemente des Netzes handelt es sich natürlich nicht um eine wirklich "stetige" Verteilung der Optimierungsvariablen:

• Die Anzahl der diskreten Parameter-Werte ist endlich, aber unbestimmt groß.
• Die Anzahl der Optimierungsvariablen hängt ab von der Feinheit des Netzes, welche im Rahmen der erforderlichen Genauigkeit beliebig geändert werden kann.

Man spricht deshalb idealisiert von einer "parameterfreien" Optimierung, wenn diese direkt am FEM-Netz angreift.

Die Vorzüge der "parameterfreien" Optimierung kommen fast ausschließlich in den Etappen der Topologie- und Form-Optimierung zur Geltung:

• Unabhängigkeit von der Parametrisierung und Qualität eines CAD-Modells.
• Unabhängigkeit vom konkreten CAD-System und eventuell erforderlichen Format-Konvertierungen zum Einbinden in das Optimierungstool.

Dem steht jedoch auch ein wesentlicher Nachteil einschließlich seiner Konsequenzen gegenüber:

• Die optimierte Struktur steht nicht als CAD-Modell zur Verfügung (nur als Netz).
• Es Bedarf eines gewissen Aufwandes, das Oberflächennetz des FEM-Modells in ein CAD-Modell zu überführen, welches ein fertigbares, ästhetisch akzeptiertes Bauteil repräsentiert.

Klassifizierung nach Art der Loesungssuche

Wie die Optimierungsparameter (Design-Variablen) zielgerichtet verändert werden, hängt vom verwendeten Optimierungsverfahren ab. Die existierenden Verfahren lassen sich grob in zwei Gruppen gliedern:

Mathematische Verfahren

Bei den mathematischen Verfahren werden die Design-Variablen aufgrund einer mathematisch hergeleiteten Gesetzmäßigkeit verändert, was dann zum Optimum führt:

• Grundlage ist die Bewertung der aktuell erreichten Lösungsgüte und oft auch die Berücksichtigung der bisherigen Lösungsschritte.
• Die Suche nach der optimalen Lösung wird dabei auf die Extremwert-Suche (meist "Minimum") einer Zielfunktion reduziert, welche die Güte der Lösung repräsentiert.

Empirische Verfahren

Bei empirischen Verfahren werden die Design-Variablen auf der Basis einer Vorschrift iterativ verändert, die auf der Vermutung der Optimalität basieren und in der Regel mit wenig Rechenaufwand gute Ergebnisse liefern:

• Ein typisches Beispiel sind die Konsequenzen aus der biologischen Wachstumsregel:
  1. Lagere an hochbelasteten Stellen Material an.
  2. Entferne Material an niedrigbelasteten Stellen.
• Empirische Verfahren können auf zwei verschiedenen Ebenen ansetzen:

1. Ergebnis-orientiert

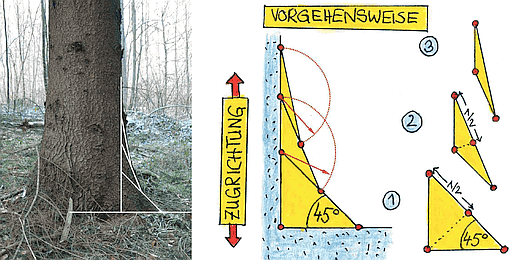
• Bei Pflanzen wirkt nur der erste Teil der Wachstumsregel. Damit überbrückt und entschärft z.B. ein Baumstamm die rechteckige Kerbe, die er mit der Erdoberfläche bildet, durch den Wurzelanlauf. Dieser Wurzelanlauf besitzt eine universelle Form, welche man auch auf andere Kerben anwenden kann!
• Zur Konstruktion dieser günstigen Kerbform kann man die sogenannte Zugdreieck-Methode verwenden (nach Claus Mattheck). Diese ermöglicht es, mittels einfacher geometrischer Operationen an Unstetigkeitsstellen der Oberfläche eine kerbspannungsminimierte Kontur zu konstruieren (Bild aus einem "Mattheck-Poster"):

2. Prozess-orientiert

• Anstatt das Ergebnis des Pflanzenwachstums an Kerbstellen durch eine Konstruktionsregel nachzubilden, kann man auch den Prozess des Wirkens des ersten Teils der Wachstumsregel auf ein FEM-Modell anwenden:
  • Das CAO-Verfahren (Computer Aided Optimization) ist ein Verfahren zur Formoptimierung, welches dieses verstärkte Wachstum an stärker belasteten Stellen der Oberfläche über mehrere Iterationen nachbildet.
  • Im Ergebnis entsteht am Ende dieses Prozesses an einer Oberflächenkerbe praktisch das gleiche Ergebnis, wie bei Anwendung des Zugdreieck-Methode.
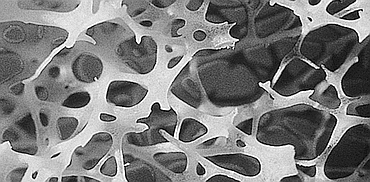
• Im Unterschied zu Pflanzen wirken in tierischen Knochen beide Teile der Wachstumsregel, da Knochenmaterial auch abbaubar ist. Das dynamische Gleichgewicht zwischen Auf- und Abbau wird durch die aktuelle lokale Belastung des Knochens gesteuert. Im Ergebnis dieses Prozesses entsteht eine Leichtbau-Struktur innerhalb des Knochens (Bild-Quelle: Wikimedia Commons):
  
  • Beim SKO-Verfahren (Soft Kill Option) wird im Unterschied zum CAO-Verfahren die Wachstumsregel nicht nur auf die Oberfläche eines Bauteils angewendet, sondern auch auf den inneren Bereich.
  • Da hierbei auch der zweite Teil der Wachstumsregel wirkt, können auch Löcher innerhalb des Bauteils entstehen. Man kann dieses Verfahren deshalb zur Topologie-Optimierung verwenden.

Generatives Design

Prozess-Schritte im generativen Design

Definition der Anforderungen

Studie mit RB, Materialien, Fertigung