Grundlagen: Probabilistik - Optimierung
Charakteristik
"Klassische" Nennwert-Optimierung bewertet die Güte einer Lösung nur auf Grundlage der "exakten Werte" von Bewertungsgrößen, welche aus den momentanen "exakten Werten" der Inputgrößen mit einem deterministischen Modell berechnet werden:
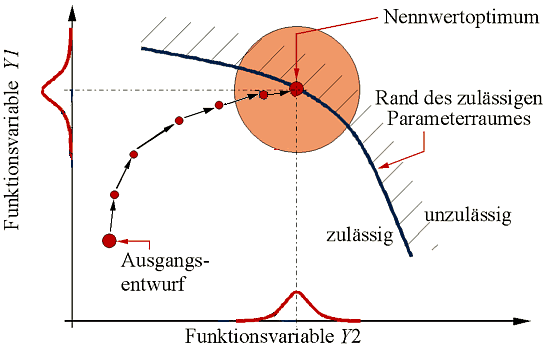
- Nennwert-otimierte Lösungen für technische Probleme liegen meist an den Restriktionsgrenzen, da die technisch-physikalischen Grenzen weitestgehend ausgenutzt werden.
- Man erhält damit nur idealisierte Lösungen, da in der realen Welt sowohl die Geometrie als auch die Stoff- und Umgebungseigenschaften mit Streuungen behaftet sind. Diese Streuungen sorgen dafür, dass meist mehr als die Hälfte aller realisierten Exemplare einer Nennwert-optimierten Lösung außerhalb der Spezifikation arbeitet:
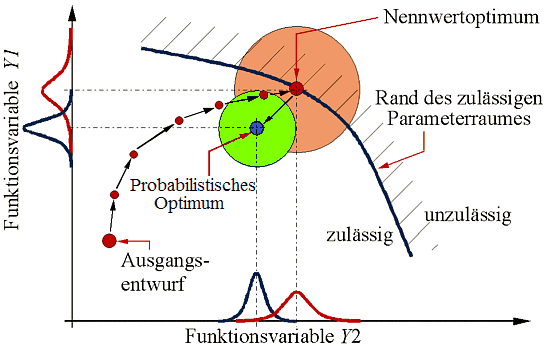
Probabilistische Optimierung soll unrealistische, idealisierte Optima vermeiden, indem zumindest ein Teil der Bewertungsgrößen für die Güte-Berechnung die immer vorhandenen Streuungen repräsentiert:
- Streuungen von Outputgrößen (Bewertungsgrößen) können nur durch die Einbeziehung der Streuungen von Inputgrößen ermittelt werden, d.h., durch probabilistische Simulation.
- Optimale Lösungen beziehen sich somit nicht auf ein einzelnes "ideales" Exemplar, sondern auf die Gesamtheit aller realisierbaren Exemplare.
- Die "besten" Exemplare innerhalb dieser optimierten Lösungsgesamtheit entsprechen dann ungefähr der Lösung aus der Nennwert-Optimierung, die "schlechtesten" Exemplare erfüllen aber auch noch alle Forderungen der Anforderungsliste:
Hinweis: Die Art des benutzten Optimierungsverfahrens ist nicht relevant für die Bezeichnung "probabilistische Optimierung". Es zählt nur die Art der Güte-Berechnung basierend auf der Streuung aller möglichen Exemplare.
Zielstellung
Es existieren im Prinzip zwei grundlegende Ziele für die probabilistische Optimierung:
- Alle produzierten Exemplare sollen im Rahmen ihrer Spezifikation möglichst gut funktionieren.
- Die Kosten für die Realisierung des ersten Zieles sollten möglichst gering sein.
In welchem Maße man diese beiden Ziele verfolgen kann, ist abhängig von:
- der Komplexität des Problems,
- der Qualität der verfügbaren Modell und
- der Verfügbarkeit sowie Qualität der Daten für die Modell-Parameter
Modellaufbereitung
Unabhängig davon, in welchem Maße man obige Ziele verfolgt, stößt man an die Grenzen der aktuell verfügbaren Rechentechnik. Um in akzeptabler Zeit eine probabilistische Optimierung durchführen zu können, muss zuvor auf Basis einer probabilistischen Analyse eine Vereinfachung des probabilistischen Modells erfolgen. Dazu hat sich die folgende heuristische Vorgehensweise bewährt:
- Finden einer optimalen Ausgangslösung:
- Vereinfachungen eines nichtlinearen Modells (z.B. Linearisierung, Parameter-Reduktion) sind nur gültig für einen relativ kleinen Bereich um einen Arbeitspunkt.
- Es wird deshalb zuerst von der Annahme ausgegangen, dass die optimale Lösung der probabilistischen Optimierung in der Nähe des Nennwert-Optimums liegt.
- Bevor man sich Gedanken zur probabilistischen Optimierung macht, sollte man also zuerst ein möglichst gutes Nennwert-Optimum ohne Berücksichtigung von Streuungen gefunden haben.
- Reduktion auf wesentliche Input-Streuungen:
- Jede berücksichtigte Streuung erfordert Modellberechnungen. Die Anzahl der erforderlichen Modellberechnungen kann in Abhängigkeit von den benutzten Ersatzmodellen auch exponentiell steigen.
- Praxisrelevante Modelle können hunderte Modellparameter besitzen. Eine erste Reduktion auf eine in der probabilistischen Analyse zeitlich beherrschbare Menge streuender Parameter sollte dann auf der Basis von Vorüberlegungen erfolgen.
- Die Reduktion der Streuungsanzahl anhand der Sensitivitäten ist für nichtlineare Modelle nur validiert im Streubereich um den Arbeitspunkt der probabilistischen Analyse, d.h., um das Nennwert-Optimum.
- Damit man mit Hilfe einer Sensitivitätsanalyse die nicht relevanten Streuungen identifizieren kann, sind realistische Annahmen zu den Streubereichen erforderlich (Toleranzen und Verteilungen).
- RSM-Minimalmodell:
- Die statistische Auswertung einer Stichprobe erfolgt bei der probabilistischen Simulation mittels Response Surface Method (RSM).
- Die dafür erforderlichen Ersatzmodelle sollten nur so komplex sein, dass Sie die Übertragungsfunktion innerhalb des betrachteten Streubereiches der Input-Größen hinreichend genau abbilden:
- Wahl einer möglichst geringen Polynom-Ordnung.
- Verzicht auf die Abbildung von Interaktionen zwischen den Input-Größen (z.B. bei den Taylorreihen der Moment-Methode).
- Überflüssige Komplexität der Ersatz-Modelle erfordert zusätzliche Modellberechnungen als Stützstellen und führt eventuell zu Welligkeiten zwischen den Stützstellen.
Aspekte
Ausschuss-Quote
Für jede mittels statistischer Versuchsplanung simulierte Stichprobe liegt eine Information zur Gesamtversagenswahrscheinlichkeit vor, welche praktisch die Ausschuss-Quote repräsentiert.
Die Zielstellung der Ausschuss-Minimierung besteht darin:
- unter Berücksichtigung der vorhandenen Input-Streuungen
- Nennwerte einer optimalen Lösung zu finden,
- sodass die Gesamtversagenswahrscheinlichkeit der Lösung möglichst Null wird (= Erfüllung aller Forderungen).
- Falls die Ausschussquote Null erreicht werden kann, wird zusätzlich versucht, die Wünsche für den Nennwert möglichst gut zu erfüllen.
Ausschuss-Minimierung entspricht also einer Nennwert-Optimierung unter Berücksichtigung der Streuungen bei der Überprüfung der Restriktionsverletzungen. Man spricht auch von "zuverlässigkeitsbasierter Optimierung", denn Zielfunktion ist die Minimierung der Versagenswahrscheinlichkeit (Ausschussquote) einer berechneten Verteilung von Produkteigenschaften.
Robustheit
Unter Robustheit versteht man die Fähigkeit eines Systems, seine Funktion auch bei Schwankung der Betriebsbedingungen aufrecht zu erhalten:
- Berücksichtigt man bei der Optimierung nur den Aspekt der Ausschuss-Minimierung, so erreicht man bereits eine "hinreichende" Robustheit der Lösung. Im Bereich der berücksichtigten Streuungen der Betriebsbedingungen erfüllen alle Exemplare der Lösung die gestellten Forderungen an die Funktion.
- Möchte man die Robustheit über dieses hinreichende Maß erhöhen, so muss man eine Quantifizierung der Robustheit bei der Optimierung berücksichtigen. Diese Quantifizierung kann man mittels der Varianz der Verhaltensstreuung durchführen.
- Die sogenannte "varianzbasierte Optimierung" als Erweiterung der "zuverlässigkeitsbasierten Optimierung" führt zu einer Maximierung der Robustheit eines Systems. Bestandteil der Zielfunktion ist dabei die Minimierung der Varianzen der für das Verhalten relevanten Streuungen der Bewertungsgrößen.
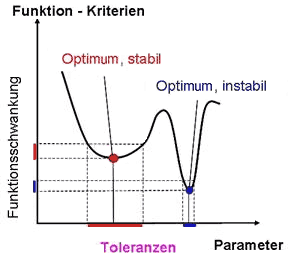
- Verringert sich bei gleichbleibenden Input-Streuungen die Varianz der Funktionsstreuung bzw. sind größere Input-Streuungen bei gleicher Funktionsstreuung zulässig, so entspricht dies einer Lösung mit einer höheren Robustheit.
- Die robustere, stabilere Lösung weist eine geringere Sensitivität in Bezug auf die Streuungen der Betriebsbedingungen auf:
Hinweis: Die varianzbasierte Optimierung zur Erhöhung der Robustheit im engeren Sinne ist nur ein Aspekt im Rahmen der sogenannten Robust-Design-Optimierung, welche besser unter dem Begriff "Design For Six Sigma" bekannt ist.
Toleranz-Kosten
Kleine Fertigungstoleranzen unterstützen eine sichere Erfüllung aller Funktionen eines Produktes. Sie sind aber sehr aufwändig und damit kostenintensiv zu realisieren. Große Fertigungstoleranzen sind zwar kostengünstig zu realisieren, führen jedoch zu einer hohen Ausschuss-Quote:
- Die Toleranz-Kosten-Optimierung hat die Minimierung der Gesamtkosten für die Realisierung aller Fertigungstoleranzen unter Einhaltung einer zulässigen Ausschussquote zum Ziel:
- Zur Lösung dieser Optimierungsaufgabe kann das Optimierungsverfahren die Toleranz-Breiten von Input-Streuungen in vorgegebenen Grenzen ändern:
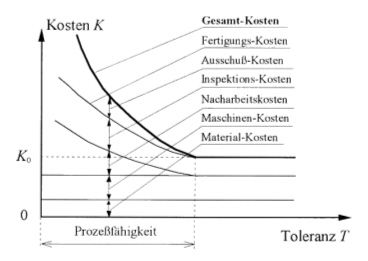
- Der Maximalwert einer Toleranz-Breite wird durch die Fix-Kosten K0 bestimmt, welche auch durch gröbere Tolerierung nicht unterschritten werden können.
- Der zugehörige Minimalwert kann anhand der technologisch-physikalischen Realisierbarkeit abgeschätzt werden.
- Problematisch ist die Gewinnung einer quantitativen Kostenfunktion für die Realisierung einer Toleranz im Variationsintervall:
- Um den Zusammenhang zwischen Toleranz und Kosten abzubilden, werden in der Literatur viele Ansätze vorgeschlagen. Allgemein gilt, dass eine Verkleinerung der Toleranzen T eine Erhöhung der Kosten K bewirkt. Wenn Toleranzen gegen null gehen, dann gehen die entsprechenden Kosten gegen unendlich. Das Toleranz-Kosten-Modell kann z.B. mit folgendem Ausdruck beschrieben werden:K = K0 + a / T
- Hat man unzureichende Informationen zu den realen Kosten, kann man sich mit einer qualitativen Abschätzung der Kostenrelationen behelfen, indem man für jede Streuung einen entsprechenden Wert für die Konstante a wählt.
- Um den Zusammenhang zwischen Toleranz und Kosten abzubilden, werden in der Literatur viele Ansätze vorgeschlagen. Allgemein gilt, dass eine Verkleinerung der Toleranzen T eine Erhöhung der Kosten K bewirkt. Wenn Toleranzen gegen null gehen, dann gehen die entsprechenden Kosten gegen unendlich. Das Toleranz-Kosten-Modell kann z.B. mit folgendem Ausdruck beschrieben werden:
- Die toleranzkosten-basierte Optimierung erfolgt mit den optimalen Nennwerten, welche zuvor durch die Ausschuss-Minimierung bzw. Robustheitsmaximierung gewonnen wurden.
- Im Ergebnis der Kosten-Minimierung ergeben sich optimale die Toleranz-Breiten derart, dass die Gesamt-Kosten für deren Realisierung möglichst klein sind und die Lösung unter Berücksichtigung aller Input-Streuungen eine vorgebende zulässige Ausschuss-Quote nicht überschreitet.
Lebensdauer
Die Lebensdauer eines Produkts wird begrenzt durch den Verschleiß und die Materialermüdung seiner Kernkomponenten.
Lebensdauer-Analyse basiert auf Modellen, welche den Verschleiß und die Materialermüdung nachbilden und daraus die kumulative Ausfallwahrscheinlichkeiten ermitteln:
- Die Auswahl geeigneter Lebensdauer-Modelle für einen konkreten Anwendungsfall ist ein wichtiger erster Schritt. Allein für mechanische Komponenten unterscheidet man z.B. fünf unterschiedliche Ansätze (basierend auf Spannung, plastischer Dehnung, Fließdehnung, Energie und Bruchmechanik):
- Spannungsbasierte Modelle verwenden die Kraft oder Spannung, die eine Dehnung der Komponenten verursacht. Typische Anwendungsfälle sind Schwingungen und mechanische Anschläge.
- Dehnungsbasierte Modelle berechnen Dehnungen aus den Spannungen innerhalb der Komponenten:
- Plastische Dehnung beruht auf zeitunabhängigen Verformungseffekten.
- Fließdehnung akkumuliert zeitabhängige Verformungseffekte.
- Energie-basierte Modelle stellen die neueste Methodik zur Lebensdauer-Analyse dar. Dabei wird die Dehnungsenergiedichte aus der Spannung-Dehnung-Hysterese der Komponenten ermittelt. Zur Lebensdauer-Berechnung wird anschließend der akkumulierte Wert der Dehnungsenergiedichte verwendet.
- Bruchmechanik-basierte Modelle betrachten die akkumulierten Materialschäden unter zyklischer Last, die durch Risse entstehen.
- In Abhängigkeit des für die Lebensdauer-Analyse gewählten Modell-Ansatzes müssen im zweiten Schritt die dafür benötigten Informationen mittels geeigneter Modelle der betrachteten Produkt-Komponenten gewonnen werden. Am Beispiel mechanischer Komponenten sind dies Finite-Element-Modelle, mit denen die Spannungs- und Dehnungsverläufe für zuvor definierte Bedingungen berechnet werden.
- Nach Übernahme der in den Komponenten-Modellen berechneten Informationen in die Lebensdauer-Modelle kann die Berechnung der Lebensdauer erfolgen. Am Beispiel mechanischer Komponenten ist dies die Übernahme der Spannungs- und Dehnungswerte aus der Finite-Element-Simulation in das gewählte Lebensdauer-Modell, mit dem dann die Anzahl der Lastzyklen bis zum Eintreten des Ausfalls ermittelt wird.
- In einem abschließenden Schritt ist die Validierung der Lebensdauer-Ergebnisse durch experimentelle Daten erforderlich, da die absolute Genauigkeit der Lebensdauer-Modelle nicht sonderlich hoch ist.