Grundlagen: Probabilistik

Dieses Kapitel wird zur Zeit erarbeitet

Vorläufige Gliederung:

• Zielstellung
• Grundbegriffe
  • Nennwert, Toleranz und Streuung
  • Statistische Versuchsplanung mit deterministischen Modellen
• ...

Zielstellung

Experimentell tätige Wissenschaftler unterliegen dem Zwang, ihre Experimente statistisch auszuwerten. Das dafür erforderliche mathematische Rüstzeug kann in dieser kurzen Einführung in die Probabilistik nicht vermittelt werden.

Im Blickfeld dieses Kapitel steht vor allem der Entwicklungsingenieur. Dieser benutzt für seine Berechnungen überwiegend "exakte" Nennwerte. Die Zulässigkeit von Toleranzen ermittelt er danach durch Analyse ihrer Grenzwerte. Damit soll z.B. die Montage oder Funktion auch unter den ungünstigsten Umständen zu 100% sichergestellt werden.

Dem Entwicklungsingenieur ist durchaus bewusst, dass Wahrscheinlichkeiten eine wichtige Rolle beim Auftreten unerwünschter Zustände in seinen Lösungen spielen. Leider sind Menschen (und damit auch Ingenieure) meist sogenannte "Wahrscheinlichkeitsidioten", die das Eintreten bestimmter Ereignisse entweder über- oder unterschätzen (zum "Idiotentest" → Geburtstagsparadoxon).

Der Entwicklungsingenieur hat kaum die Zeit, sich die benötigten mathematischen Methoden tiefgründig anzueignen und sie auf seine Probleme analytisch anzuwenden. Er ist deshalb auf vorhandene Software-Pakete angewiesen, um seine Lösungen einer probabilistischen Analyse zu unterziehen.

Anliegen dieses Kapitels ist die Vermittlung des qualitativen Wissens zu den wahrscheinlichkeitstheoretischen Grundlagen, welche für die qualifizierte Anwendung von Probabilistik-Tools erforderlich ist.

Grundbegriffe

Nennwert

In Anlehnung an den Begriff Nennmaß soll unter Nennwert der geplante Wert für eine physikalisch-technische Größe im weitesten Sinne verstanden werden. Es handelt sich hierbei um einen idealisierten, "exakten Wert", z.B.:

• Physikalische Größe als Produkt aus Maßeinheit und Zahlenwert (Skalar, Vektor, höherstufiger Tensor)
• Geometrisches Element (Punkt, Kurve, Fläche, Körper)
• Funktionale Abhängigkeit (Kennlinie, Kennfeld, Übertragungsfunktion)

Die idealisierten Nennwerte bilden die Grundlage bei der Entwicklung optimaler Lösung für technische Aufgabenstellungen. Dafür gibt es plausible Gründe:

• Physikalische Effekte außerhalb der Quantenmechanik werden mathematisch als Verknüpfung zwischen den aktuellen Istwerten der beteiligten physikalischen Größen beschrieben (Klassische Physik).
• Praktisch sämtliche CAE-Systeme arbeiten mit deterministischen Modellen (basieren auf Effekten der klassischen Physik und euklidischen Geometrie).
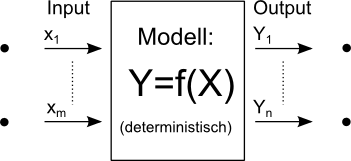
• Deterministische Modelle erzeugen aus "exakten" Eingangsgrößen mittels eindeutiger Übertragungsfunktionen "exakte" Ausgangsgrößen:

Toleranz

Ein exakter Nennwert ist praktisch nie realisierbar. Deshalb muss für jeden Nennwert ein Wertebereich definiert werden, dessen Einhaltung garantiert, dass die Funktionalität der Lösung gewährleistet ist. Diesen zulässigen Wertebereich bezeichnet man als Toleranz.

Toleranzen werden definiert über ihre Grenzen. Im Spezialfall (z.B. Press-Passungen) liegt der Nennwert außerhalb der Toleranz-Grenzen.

Man unterscheidet wie bei den "Nennwerten" unterschiedliche Toleranz-Typen:

• Maßtoleranzen, Bauteil-Toleranzen (z.B. Kennwerte von einfachen elektronischen oder mechanischen Bauelementen)
• Form- und Lagetoleranzen sowie Oberflächenangaben
• Funktionale Toleranzen (Material-Kennlinien, Wandler-Kennfelder, Übertragungsfunktionen)

Streuungen

Toleranzangaben beziehen sich nur auf die zulässigen Grenzwerte für einen Nennwert. Die tatsächlich auftretenden Istwerte treten je nach Herkunft (z.B. Fertigungsverfahren, Umweltbedingungen, Alterung) innerhalb des Toleranzfeldes mit unterschiedlichen Verteilungsfunktionen auf. In Erweiterung des Toleranz-Begriffes wird für die statistische Analyse von Ausfallwahrscheinlichkeiten der Begriff der "Streuung" benutzt.

Eine Streuung ist definiert durch

• die Toleranz (d.h. die Grenzwerte) und
• die Verteilungsdichte-Funktion im Toleranz-Feld