Software: FEMM - Stromfluss - Current-Flow-Problem

↑

← →

← FEM-Tutorial

Simulation des ungetrimmten Widerstands

- Current Flow Problem -

Mit unseren Erfahrungen zur Simulation elektrostatischer Felder mittels FEMM sollte es nun kein Problem mehr darstellen, elektrische Flussfelder als "Current Flow Problem" in FEMM zu berechnen. Wir benutzen für das Modell des ungetrimmten Widerstands die folgenden Werte:

• Depth = 20 µm (Schichtdicke)
• R_u = 171 Ω (Ungetrimmter Nennwert)
• B_u = 2,0 mm (Breite ungetrimmter Widerstand)
• L = 3,42 mm (Länge ungetrimmter Widerstand)
• R_F = 100 Ω/□ (Flächenwiderstand der Paste)

  Abweichung = -xx % (xx = Teilnehmer-Nr.)

Hinweis:

Der zu realisierende ungetrimmte Widerstand von R_u=171 Ω besitzt eine Fertigungstoleranz σ_F=±30 %. Wir arbeiten im Folgenden entsprechend der individuellen Teilnehmer-Nummer (xx) mit einem "konkreten" Widerstand R₀, der sich aus R_u=171 Ω bei einer Abweichung von −xx% ergibt.

Für die Definition des Pasten-Materials im Finite-Elemente-Modell benötigen wir die spezifische Leitfähigkeit. Diese kann man über die Dimensionierungsgleichung aus dem Flächenwiderstand berechnen:

• Angenommen wird ein Quadrat mit der Kantenlänge B und der Dicke d (bei uns d=20 µm).
• Dieses besitzt den Flächenwiderstand der gewählten Paste.
• Wir müssen bei der Berechnung der konkreten spezifischen Leitfähigkeit κ die Verringerung von R_F um xx% berücksichtigen!

[math]\displaystyle{ R_{F}=\frac{\varrho\cdot l}{A}=\frac{B}{\kappa\cdot B\cdot d} }[/math]

[math]\displaystyle{ \kappa=\frac{1}{R_{F}\cdot d} }[/math]

Material-Eigenschaften:

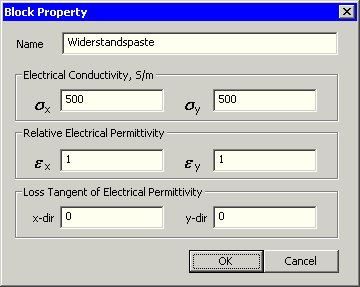
• Das Pasten-Material wird über seine spezifische elektrische Leitfähigkeit κ [S/m] definiert, welche als σ_x bzw. σ_y bei Bedarf auch in die einzelnen Richtungen unterschiedlich groß angegeben werden könnte:

• Die elektrische Fluss-Domäne berücksichtigt nicht nur den ohmschen Widerstand der Materialien, sondern kann diese als komplexe Impedanzen mit ohmschen und dielektrischen Verlusten behandeln:
  • Die dielektrische Leitfähigkeit kann in Form einer richtungsabhängigen relativen Permittivität beschrieben werden.
  • Die richtungsabhängigen Umpolarisierungsverluste des Dielektrikums werden bei Bedarf als komplexe Zahlen beschrieben:

    [math]\displaystyle{ \varepsilon=|\varepsilon|\cdot\left(\cos\phi-j\cdot\sin\phi\right) }[/math]

  • Der Winkel Phi der Zeigerdarstellung dieser komplexen Zahl ist der "Verlustwinkel". Anzugeben ist der Wert des Tangens dieses Winkels:

    [math]\displaystyle{ loss\, tangent=\frac{\sin\phi}{\cos\phi} }[/math]

Geometrie, Netz, Randbedingungen:

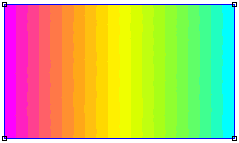
• Nur das Rechteck der aufgetragenen Paste ist in Form eines geeigneten FE-Netzes zu modellieren:

• Wichtig: Man beachte die Hinweise zum Abschalten des Smart Meshing!
• Die Kontaktierung an den beiden Seiten sollte man jeweils über ein Leiterpotential (Conductor) realisieren:
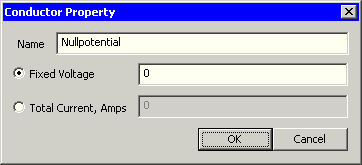
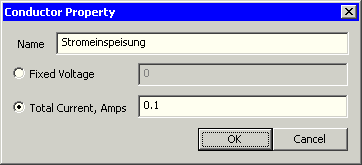
  • Über die Conductor-Properties kann man entweder ein Spannungspotential oder einen Strom vorgeben.
  • Es ist im Sinne der Widerstandsberechnung günstig, auf der einen Seite ein Nullpotential vorzugeben:
    
  • Auf der anderen Seite speist man einen Strom ein. Dieser kann auf einen technisch sinnvollen Wert gesetzt werden. Bei 0.1 A sollte man sich bewusst sein, dass damit eine größere Verlustleistung als 0.2 W erreicht wird:
    
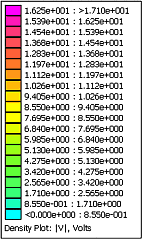
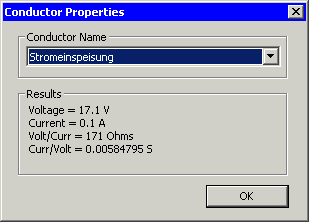
  • Der Solver berechnet für jeden Leiter den jeweils fehlenden Wert von Spannung oder Strom. Zusätzlich werden die Quotienten aus Strom und Spannung im Sinne von Widerstand bzw. Leitwert gebildet:
    
• Es sollte ziemlich exakt der über die Dimensionierungsgleichung berechenbare Widerstandswert auch mit dem FEM-Modell berechnet werden!

← →

← FEM-Tutorial