Software: FEM - Tutorial - 3D-Mechanik - Axialsymmetrie

Axial-symmetrische Volumen-Elemente

Unabhängig von den Begrenzungen der verwendeten Demoversion stößt man bei Körpern sehr schnell auf das Problem, dass man eine erforderliche feinere Vernetzung nicht mehr realisieren kann, weil die Berechnungszeit für das Modell zu lang wird.

Bei axialsymmetrischen Modellen besteht die Möglichkeit, mit speziellen Elementen nur eine radiale Schnittebene zu modellieren. Diesen Ansatz wollen wir im Folgenden benutzen. Dazu definieren wir ein neues Modell (File - New). Wir vergeben dafür den Bezeichner Gummipuffer2_xx.MOD (File - Save).

Im Grafik-Bereich erscheint für das neue Modell eine neue Register-Karte. Die Register sind nun zusätzlich mit dem Modell-Namen beschriftet. Unter "Modell Info" wird das Modell dargestellt, welches zur aktiven Register-Karte gehört.

Im Sinne der Übersichtlichkeit wählen wir das fertige Volumen-Modell und schließen es (File - Close).

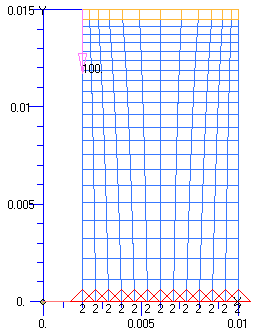
Wie bereits bei der Analyse der Symmetrie-Eigenschaften angesprochen, würde es in unserem Beispiel ausreichen, ein ganz dünnes "Tortenstück" aus z.B. der oberen Pufferhälfte zu modellieren und zu berechnen. Für solche "unendlich dünnen" Tortenstücke existiert eine besondere Form von Solid-Elementen - das "Axisymmetric Element". Dieses kann man handhaben wie ein Flächenelement:

Man vernetzt damit die Schnittfläche des "Tortenstücks" in der XY-Ebene des Koordinatensystems.
Die Y-Achse bildet dabei die Symmetrieachse des 3D-Körpers (d.h. die vernetzte 2D-Fläche rotiert um die Y-Achse, die X-Koordinate entspricht demzufolge dem Radius).
Die zu vernetzende 2D-Fläche muss im I. und/oder IV. Quadranten liegen (d.h. sie darf keine negativen X-Koordinaten der Knoten aufweisen!).
Die stetige Erhöhung der differentiell kleinen Dicke mit wachsendem Abstand von der Symmetrie-Achse wird automatisch berücksichtigt.
Im Unterschied zu "richtigen" Solid-Elementen benötigen Axisymmetrische Elemente näherungsweise nur soviel Knoten wie Flächen-Elemente.
Mit relativ wenigen Knoten und Elementen gelingt eine feinmaschige Behandlung des räumlichen Problems.

Mit unseren Kenntnissen zum Mapped Mesher beginnen wir nun die Arbeit an dem neuem Modell:

Wir konfigurieren die Arbeitsfläche.
Als Grundlage für den Mapped Mesher erstellen wir die erforderlichen Boundary Surfaces(Stahlscheibe und Gummi).
Achtung: Zusammenfassen koinzidenter Linien und Punkte nicht vergessen!
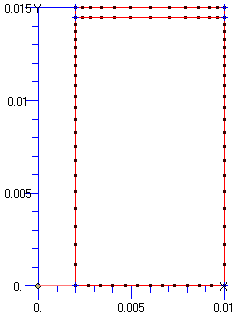
Mit den möglichen 300 Knoten der Demo-Version könnte man das Netz wie folgt gestalten:
- Radial mit 12 Elementen vernetzen (=13 Knoten).
- Damit stehen in der Höhe 23 Knoten zur Verfügung (13x23=299), das entspricht 22 Element-Reihen.
- Die Stahlscheibe vernetzen wir nur mit 1 Elementschicht.
- Der Gummi erhält somit 21 Elementschichten.
Die kritischen Stellen am Loch- und Außenrand der Stahlscheibe sollen enger vernetzt werden:
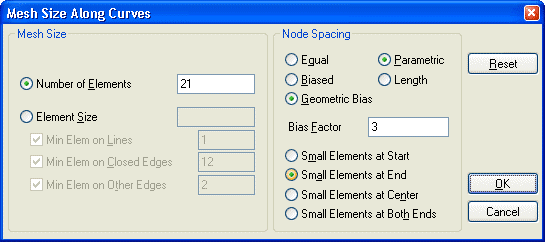
- Wir steuern dies über einen geometrischen Bias-Faktor=3 (Bias .. englisch für "Verzerrung") beim Festlegen der Elemente-Anzahl pro Viereck-Kante (Size Along Curve). Hier am Beispiel der Höhenteilung des Gummi:
- Leider kann man nur Raten, wo an den Linien sich Start bzw. End befinden. Deshalb sollte man über die View Quick Options <Strg> alle störenden Elemente in der Darstellung ausblenden. Entspricht die Darstellung des Rate-Ergebnisses nicht den Erwartungen, so kann man die Element-Einteilung der Linien jederzeit ändern.
- Die radialen Kanten der Teilnetze verzerren wir analog dazu nur an der Stahlscheibe (Small Elemets of Both Ends).

Hinweis: Leider kann man in der Demo-Version die maximal mögliche Element-Anzahl nur über einen Trick erreichen:

Vernetzt man Stahl-Scheibe und Gummi nacheinander, so entstehen 312 Knoten. Die koinzidenten Knoten kann man dann nicht mehr zusammenführen!
Wir vernetzen deshalb beide Bereiche vorerst mit einer gemeinsamen Element-Property (z.B. Gummi).
Mittels (Modify - Update Elements - Property ID) ersetzen wir dann in den Elementen der Stahlscheibe die Gummi-Property durch die Stahl-Property.

Wir bilden mit dem axial-symmetrischen Modell alle Lastfälle des Volumenmodells nach.

===>> Hier geht es bald weiter !!!

Dieser Übungskomplex wurde noch nicht vollständig implementiert. Fortsetzung im Original der Übungsanleitung: http://www.ifte.de/lehre/cae/fem/02_mechanik3d/axisymmetric.html

← →

http://translate.google.de/translate_tools?hl=de&sl=de