Software: FEM - Tutorial - Einleitung: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung |
||
| Zeile 12: | Zeile 12: | ||
* Temperaturen | * Temperaturen | ||
* Verläufe elektrischer und magnetischer Felder | * Verläufe elektrischer und magnetischer Felder | ||
Damit kann man sowohl die Belastung des betrachteten Objekts als auch seine Wirkung auf die Umgebung berechnen. | |||
Deshalb wird die praktische Anwendung dieser Methode für Konstrukteure sehr interessant, wenn da nicht die Hürden der Mathematik wären! Jede Einführung zur FEM führt unweigerlich über die grundlegenden Vektordifferentialgleichungen und über die Verfahren ihrer numerischen Lösung. | |||
Version vom 26. Februar 2009, 13:17 Uhr
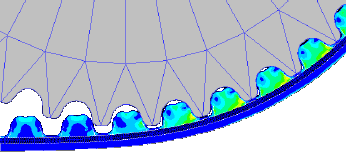
Die Finite-Elemente-Methode (FEM) ist ein numerisches Verfahren zur näherungsweisen Lösung von partiellen Differentialgleichungen mit Randbedingungen.
Die Lösungen dieser partiellen Differentialgleichungen beschreiben die räumliche und auch zeitliche Verteilung der zugehörigen physikalischen Größen in einem betrachteten Raumgebiet. Man erhält im Ergebnis für das Innere eines räumlichen Objektes z.B.:
- mechanische Spannungen und Verformungen
- Drücke und Strömungen
- Temperaturen
- Verläufe elektrischer und magnetischer Felder
Damit kann man sowohl die Belastung des betrachteten Objekts als auch seine Wirkung auf die Umgebung berechnen.
Deshalb wird die praktische Anwendung dieser Methode für Konstrukteure sehr interessant, wenn da nicht die Hürden der Mathematik wären! Jede Einführung zur FEM führt unweigerlich über die grundlegenden Vektordifferentialgleichungen und über die Verfahren ihrer numerischen Lösung.