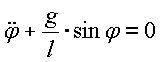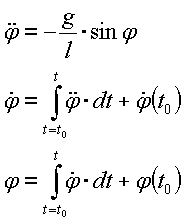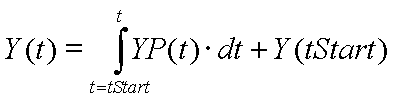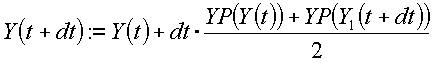Grundlagen: Simulation - Solver

Autor: Dr.-Ing. Alfred Kamusella

Simulationen mit numerischen Modellen beruhen im Wesentlichen auf der Berechnung von Modell-Ergebnissen mit Hilfe eines Gleichungslösers (Solver). In diesem Grundlagen-Kapitel liegt der Schwerpunkt auf der Erläuterung der prinzipiellen Wirkungsweise von Solvern zur Simulation dynamischer Systeme im Zeitbereich. Dabei wird beispielhaft Bezug genommen auf die Begriffe und Konzepte, wie sie im Simulationssystem SimulationX verwendet werden.

Numerische Simulation zeitkontinuierlicher Systeme

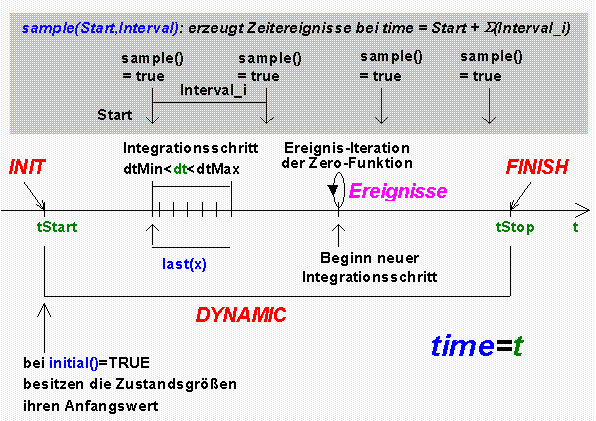
Kenngrößen eines Simulationslaufes (Zeitachse)

• Aus Sicht des Modells läuft die Simulationszeit time bzw. t in diskreten Schritten dt von tStart bis tStop (meist vorwärts):
  
• Innerhalb des aktuellen Zeitintervalls dt werden in Abhängigkeit vom verwendeten Lösungsverfahren mehrere Stützstellen berechnet:
  • Jede Stützstelle entspricht einer einmaligen Modellberechnung. Demzufolge sind die meisten Modelldurchrechnungen Hilfsrechnungen (mit "unexakten" Werten).
  • Nach Durchführung aller Hilfsrechnungen erfolgt einmalig für das Ende des aktuellen Zeitintervalls dt eine Modellberechnung mit den "richtigen" Modellwerten.
  • Innerhalb des Modell-Algorithmus kann man auf die letzten "richtigen" Modellwerte zugreifen (in SimulationX mit der last-Funktion).
• Bei numerischen Verfahren mit Schrittweitenregelung erfolgt eine automatische Anpassung der Schrittweite dt an die Eigenschaften des Modells zum berechneten Zeitpunkt ("Wie schnell können sich die physikalischen Zustandsgrößen ändern?"):
  • Je empfindlicher Zustandsgrößen des Modells auf andere Modellgrößen reagieren können, desto kleiner wird dt gewählt.
  • Die zulässige Rechenschritte dt kann man begrenzen (dtMin soll "ewiges" Rechnen vermeiden / dtMax soll eckige Signalverläufe vermeiden).
• Die Berechnung mit der sich kontinuierlich anpassenden Schrittweite dt wird gestört durch Ereignis-Zeitpunkte, welche "exakt" angesteuert und berechnet werden müssen. Die Wirkungsweise der erforderliche Ereignisbehandlung wird in einem gesonderten Abschnitt erläutert.

Abschnitte eines Simulationslaufes

Ein Simulationslauf im Zeitintervall tStart ≤ time ≤ tStop besteht aus den Abschnitten INIT, DYNAMIC und FINISH. Im Folgenden wird die Aufgabe dieser Abschnitte zum einen aus numerischer Sicht erläutert. Zum anderen erfolgen Hinweise, welche Aufgaben die zugehörigen Modellabschnitte für die Nutzung von Modellen im Konstruktionsprozess übernehmen:

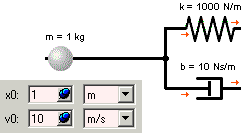
INIT ( time = tStart )
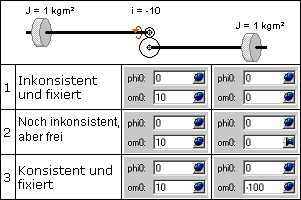
dient der Ermittlung konsistenter Anfangswerte für alle Zustandsgrößen (Bilder aus der SimulationX-Hilfe):

• Die Anfangswerte charakterisieren den (energetischen) Zustand des Modells zu Beginn der Simulation.
• Anfangswerte gewöhnlicher DGL sind immer konsistent (ODE: Ordinary Differential Equation). Der Solver kann daraus eindeutig die Werte der höchsten Ableitungen berechnen (im Beispiel Beschleunigung a(tStart)=-1100 m/s²).
• Modelle mit Zwangsbedingungen (z.B. für Getriebe) führen zu Algebro-Differenzialgleichungen (DAE: Differential Algebraic Equation). Hier können einige Zustandsgrößen nicht unabhängig voneinander gewählt werden:
  
• Man muss sich entscheiden, welche Anfangswerte man definiert vorgibt (fixiert). Die nicht fixierten Anfangswerte versucht der Solver, aus den im Modell in Form von Gleichungen beschriebenen Zwangsbedingungen zu berechnen. Dies gelingt insbesondere bei stark nichtlinearen oder nicht nichteindeutigen Zusammenhängen nicht immer!
• Man sollte möglichst viele gültige Anfangswerte vorgeben und fixieren! Nur dort, wo die analytische Berücksichtigung der Abhängigkeiten praktisch unmöglich ist, überlässt man dem Solver die Anfangswertbestimmung!

Idealisierte Netzwerkelemente besitzen konzentrierte Parameter (Punktmasse, Elastizität, Widerstand usw.):

• Über die Dimensionierungsgleichungen der Elemente ist eine Transformation konstruktiver Kenngrößen (Geometrie und Stoffeigenschaften) in die erforderliche konzentrierten Parameter möglich.
• Für die zeitunabhängigen konzentrierten Parameter sollte diese Dimensionierungsgleichungen in den INIT-Abschnitt der Modell implementiert werden. Es entstehen dadurch Modell-Elemente, welche mit konstruktiven (stofflich-geometrischen) Parametern gespeist werden (Abmessung, Dichte, E-Modul usw.).

DYNAMIC ( tStart ≤ time ≤ tStop )
Es wirkt die Überführungsfunktion des dynamischen Systems (DGL=dynamisches Modell):

• Die numerische Lösung des DGL-Systems berechnet die zeitliche Entwicklung aller Zustandsgrößen in Form von Signalverläufen.
• Alle Modellgrößen, deren Werte von den Zustandsgrößen abhängig sind, werden ebenfalls als Signalverläufe berechnet.
• Die mit dem Modell berechneten Signalverläufe repräsentieren das zeitliche Verhalten des abgebildeten Originals.

FINISH ( time = tStop )
ermöglicht die abschließende Berechnung integraler Werte (z.B. mittlere Verlustleistung, Statistik, Fourieranalyse):

• Im FINISH-Abschnitt des Modells sollte die automatisierte Auswertung der im DYNAMIC-Abschnitt berechneten Signalverläufe implementiert werden.
• Wichtig für die weitere Verwertung der Simulationsergebnisse im Konstruktionsprozess sind Bewertungsgrößen, welche die Qualität des Modellverhaltens repräsentieren (z.B. Wirkungsgrad oder Kosten aus Material- und Energieverbrauch). Möglich wäre hier auch eine "ästhetische" Bewertung im Sinne der Eleganz des Bewegungsablaufs in einem Antrieb.

Ableitungs- und Integralform von DGL

Die Überführungsfunktion eines dynamischen Modells stellt ein DGL-System dar. Zur Lösung dieses DGL-Systems verwenden die Solver Verfahren der numerischen Integration:

• Zweck der Verfahren zur numerischen Integration ist die näherungsweise Berechnung der Fläche (bestimmtes Integral) unter einem Funktionsverlauf (Ableitung).
• Es existieren zwei grundsätzliche Möglichkeiten, um ein DGL-System zu notieren (hier am Beispiel des Pendels):
  1. Ableitungsform:
     
  2. Integralform:
     
• Die Integralform enthält explizit die Zustandsgrößen als Ergebnis einer numerischen Integration. Insofern ist diese Form für den technischen Anwender meist anschaulicher als die Ableitungsform.
• Unabhängig von der im Modell gewählten Notation erfolgt durch das Simulationssystem für den Anwender unsichtbar eine Transformation in die für den Solver geeignete Form eines DGL-Systems.

Wechselwirkung von Zustandsgroesse Y und Ableitung YP

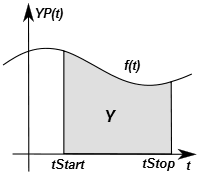
Y(t) als Resultat einer Integral-Bildung kann geometrisch als Fläche unter dem Funktionsverlauf der zugehörigen Ableitung YP(t) interpretiert werden:

• Y(t) repräsentiert in einem dynamischen Modell die Füllung eines Speicher-Elements mit Energie, Stoff bzw. Information (=Zustandsgröße). YP(t) ist dabei die Änderungsgeschwindigkeit dY/dt für die Füllung des Speicherelements.
• Im Allgemeinen ist YP(t)=f(Y(t)), d.h. die Geschwindigkeit des Energie- /Stoff- /Info- Flusses zwischen den Speichern ist abhängig von den Potentialdifferenzen und den Übertragungselementen zwischen den Speichern.
• Da YP(t) somit nicht explizit gegeben ist, kann Y(t) nicht hinreichend genau durch numerische Verfahren der Flächenberechnung ermittelt werden (z.B.: Trapez- /Tangentenformel oder Simpsonsche Regel).
• Die konkreten zeitlichen Verläufe von Y(t) und YP(t) ergeben sich erst durch die zeitliche Wechselwirkung zwischen den Energiespeichern!

Zentraler Integrationskern (Solver)

Es existieren verschiedene Verfahren zur Lösung (=Simulation) von DGL mittels numerischer Integration. Diese Verfahren sind meist in einem "zentralen Integrationskern" = "Solver" implementiert:

• Die Integral- bzw. Differential-Funktion ist die Grundlage für die Verbindung zwischen Modell und Solver:

:
a  := F/(m);
v  := integral (a,v0);
x  := integral (v,x0);

• Es sieht auf den ersten Blick so aus, als würde über diese Funktionsaufrufe der zentrale Integrationskern vom Modell aus aufgerufen, jedoch verhält es sich umgekehrt!
• Das Modell ist aus Sicht der numerischen Integration eine Black-Box, welche die Ableitungen der Zustandsgrößen berechnet:
  

Prinzip der numerischen Integration

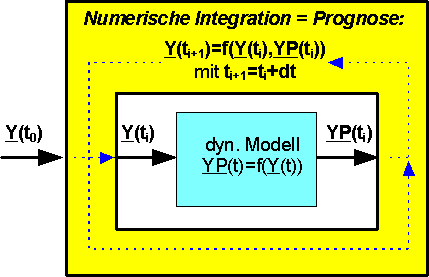
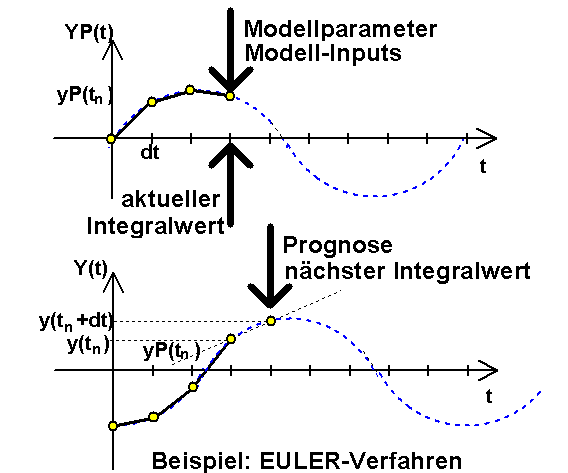
Das DGL-System wird durch die numerische Integration zum "Leben" erweckt. Es entwickelt eine Eigendynamik auf der Basis seiner Elemente (Speicher, Übertragungsglieder und Wandler) und ihrer Wechselwirkung. Der Solver ist in der Lage, über einen begrenzten zeitlichen Prognosehorizont den Zustand des Systems hinreichend genau vorauszusagen:

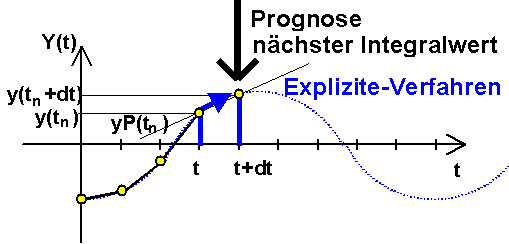
• Ausgehend von den Werten der Zustandsgrößen und Eingangssignale zum aktuellen Zeitpunkt t_n sowie den Modellparametern werden mit dem Modell die zeitlichen Ableitungen YP(t) der Zustandsgrößen Y(t) ermittelt.
• Mit dieser "Abschätzung" der zeitlichen Änderung der Zustandsgrößen prognostiziert der Solver über das Zeitintervall dt die Werte der Zustandsgrößen für den Zeitpunkt t_n+dt.
• Im obigen Bild wird dies am Beispiel des EULER-Verfahrens verdeutlicht. Bei diesem Verfahren wird vereinfachend angenommen, dass die Ableitung der Zustandsgrößen im Zeitintervall dt konstant auf dem Wert YP(t) bleibt.
• Nach der Art und Weise, wie die Prognose der Zustandsgrößen für den nächsten Integrationsschritt dt erfolgt, kann man die Verfahren der numerischen Integration grob in grundsätzliche Klassen einteilen. Diese Klassifizierung der Integrationsverfahren soll in den folgenden Abschnitten kurz vorgestellt werden.

Explizite und implizite Verfahren

• Zum aktuellen Zeitpunkt t_n können mit dem dynamischen Modell die aktuellen zeitlichen Ableitungen der Zustandsgrößen berechnet werden:

• Der effektive Wert der Ableitung der Zustandsgrößen gemittelt über das gesamte Intervall dt wird unabhängig von der Einteilung in explizit/implizit durch Hinzunahme weiterer Informationen "geschätzt". Die Prinzipien dieser Abschätzung werden in den folgenden Abschnitten noch erläutert.

Explizite Verfahren betrachten den Schätzwert für die effektive Ableitung YP als hinreichend genau. Grafisch stellt sich die Prognose einer Zustandsgröße für den Zeitpunkt t_n+dt als Anstieg der Tangente YP an die Zustandsgröße YP(t_n) im Intervall dt dar:

• Der prognostizierte Wert der Zustandsgrößen wird dann ebenfalls als hinreichend angenommen und ist Ausgangspunkt für die Berechnung des nächsten Zeitschrittes dt.

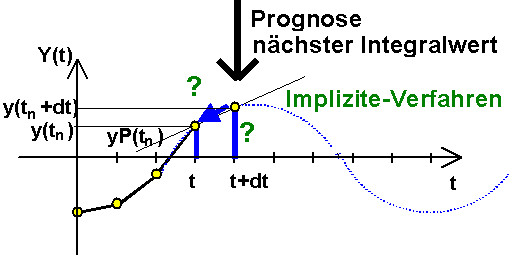
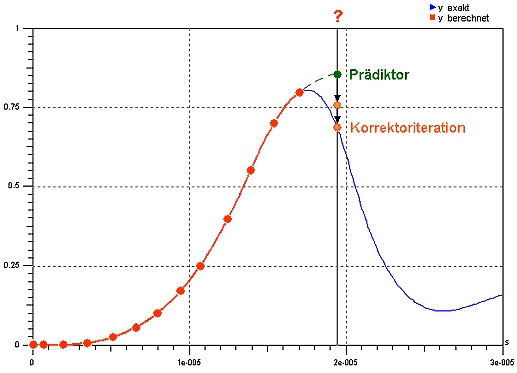
Implizite Verfahren bewegen sich im Zeitbereich nicht so geradlinig vorwärts wie explizite Verfahren. Die Berechnung jedes Zeitschrittes dt ist durch eine Iterationsschleife gekennzeichnet:

• Unter Berücksichtigung des berechneten Anstiegs YP(t_n) wird ein Anfangswert für die Zustandsgröße am Ende des Zeitschrittes dt Y(t_n+dt) abgeschätzt (z.B. durch Extrapolation des bisherigen Signalverlauf Y(t)).
• Der mit dem aktuellen Wert von Y(t_n+dt) mittels des dynamischen Modells berechnete Anstieg YP(t_n+dt) wird als Tangente an Y(t_n+dt) angelegt und rückwärts zum aktuellen Zeitpunkt t_n verfolgt.
• Ziel der anschließenden Iteration ist die Verbesserung des Schätzwertes für Y(t_n+dt) solange, bis die rückwärts verfolgte Tangente YP den Wert von Y(t_n) hinreichend genau trifft.
• Ist dieses Ziel erreicht, werden die aktuellen Werte der Zustandsgrößen Y(t_n+dt) als hinreichend genau angenommen und das Integrationsverfahren beginnt mit der Berechnung des nächsten Zeitschrittes dt.

Einschritt- und Mehrschritt-Verfahren

Unabhängig von der Einteilung in explizite und implizite Verfahren existiert eine Unterteilung in die sogenannten Einschritt- und Mehrschritt-Verfahren.

Einschritt-Verfahren

• "Betrachten" für die Prognose des nächsten Systemzustandes (Zeitpunkt=t_n+dt) ausgehend von Y(t_n) nur den aktuell auszuführenden Zeitschritt dt.
• Je nach Genauigkeitsordnung des konkreten Verfahrens wird eine Anzahl von Systemabtastungen innerhalb dieses Zeitschrittes durchgeführt (=Modellrechnungen).
• Nach der erfolgreichen Prognose für Y(t_n+dt) rückt das vom Verfahren betrachtete Zeitfenster um dt weiter.
• Da nur Informationen aus dem aktuellen Simulationsschritt verwendet werden, sind starke Änderungen der dynamischen Beziehungen relativ unproblematisch (Schrittweitenregelung).

Mehrschritt-Verfahren

• Durch Bestimmung eines Interpolationspolynoms, das durch zurückliegende Zeit-Stützpunkte der Lösungsfunktion gelegt wird, kann deren weiterer Verlauf prognostiziert werden.
• Es wird zwischen reinen Mehrschrittverfahren (Adams-Bashforth-Verfahren) und den Prädiktor-Korrektor-Verfahren unterschieden.
• Bei Prädiktor-Korrektor-Verfahren wird der extrapolierte Wert der Lösungsfunktion in mehreren Iterationen korrigiert (implizites Verfahren).
• Bei stetigen Modellen benötigen Mehrschritt-Verfahren weniger Abtastungen als Einschritt-Verfahren und sind somit schneller.
• Bei Unstetigkeiten geht dieser Vorteil durch die ständigen Wiederanlaufphasen schnell verloren (erste Schritte mit Einschritt-Verfahren!).

Beispiele fuer Integrationsverfahren

Im Folgenden soll exemplarisch die Wirkungsweise wichtiger Verfahren der numerischen Integration vorgestellt werden. Aus der unterschiedlichen Wirkungsweise resultieren die unterschiedlichen Eigenschaften der Integrationsverfahren. Dieses Wissen ist nützlich, wenn man für ein konkretes Modell ein geeignetes Verfahren der numerischen Integration auswählen und konfigurieren muss.

Explizite Einschritt-Verfahren

Das EULER-Verfahren ist das einfachste Verfahren:

• Man nimmt an, dass die Änderungsgeschwindigkeit YP der Zustandsgrößen Y über die Zeitspanne dt hinweg konstant bleibt:
  
• Infolge der Aufsummierung der Prognosefehler wird das EULER-Verfahren sehr schnell instabil!

Beim HEUN-Verfahren wird ein Korrekturschritt angefügt:

• Mit der nach EULER prognostizierten Zustandsgröße Y₁(t+dt) berechnet man die Ableitung YP(Y₁(t+dt)).
• Dann nimmt man den Mittelwert beider Ableitungen als genauere Annahme für den Anstieg YP(t):
  
• Der Berechnungsaufwand für einen Zeitschritt dt verdoppelt sich im Vergleich zum EULER-Verfahren.
• Infolge der verbesserten "Abschätzung" der effektiven Ableitung im Zeitintervall dt ist jedoch der Prognosefehler um Größenordnungen geringer als beim EULER-Verfahren und das Verfahren arbeitet auch mit größeren Schrittweiten dt wesentlich stabiler als das EULER-Verfahren.

Verallgemeinerung für explizite Runge-Kutta-Verfahren :

• Das EULER- und HEUN-Verfahren sind Runge-Kutta-Verfahren 1. bzw. 2. Ordnung.
• Je nach Ordnung des konkreten Runge-Kutta-Verfahrens wird der Funktionswert YP(t) auf der Basis mehrerer Stützstellen (Modellrechnungen) im betrachteten Zeitschritt "geschätzt":
  
• Die Zahl der erforderlichen Stützstellen steigt mit der Ordnung des Verfahrens. Mit der Ordnung des Verfahrens steigt auch die Genauigkeit der Berechnung.
• Durch Ermittlung von YP(t) mittels zweier unterschiedlicher Genauigkeitsordnungen kann eine Fehlerabschätzung und Schrittweitenregelung erfolgen. Man spricht hierbei von eingebetteten Verfahren, weil für das Verfahren der niedrigeren Ordnung eine Teilmenge der Stützstellen der höheren Ordnung verwendet werden.

Implizite Mehrschritt-Verfahren

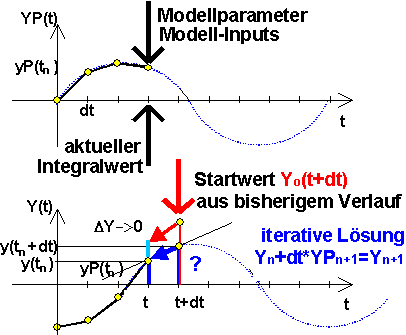
• Bei den BDF-Verfahren (Backward-Differential Formulas) handelt es sich um implizite Verfahren mit einstellbarer Ordnung und automatischer Schrittweitensteuerung:
  
• Auf Grundlage des bereits berechneten Verlaufs der Zustandsgröße Y(t) bis zum Zeitpunkt t erfolgt eine Startwert-Ermittlung Y_o(t+dt) als Ausgangspunkt für die "exakte" Lösung Y(t+dt) je nach Ordnung des Verfahrens:
  
• Danach erfolgt eine iterative Lösung des nichtlinearen Gleichungssystems zur Berechnung der Zustandsgrößen Y(t+dt) mit Abbruch bei der geforderten Genauigkeit.

Die BDF-Verfahren sind sogenannte Prädiktor-Korrektor-Verfahren:

• Für jede Zustandsgröße wird bei einer Verfahrensordnung k aus k+1 bereits berechneten Werten der nächste aktuelle Wert als Anfangswert Y_o(t+dt) extrapoliert (Prädiktor = Prognose durch explizites Mehrschrittverfahren).
• Der Wert Y(t+dt)wird iterativ durch ein implizites Mehrschrittverfahren gleicher Ordnung so lange verbessert, bis bestimmte Konvergenzkriterien erfüllt sind (corrector = Verbesserer):
  
• In jeder Korrektor-Iteration muss ein lineares Gleichungssystem gelöst werden:

res = J · (Y_i-1 - Y_i)

mit res = Residuen / J = Jacobimatrix / Y = Zustandsgrößen

• Das Residuum widerspiegelt den momentanen Fehler in den Differentialgleichungen.
• Nach jeder Iteration wird die zu Y_i gehörende Ableitung mittels Modellberechnung ermittelt und "rückwärts" überprüft, ob damit Y_i-1 erreicht wird (implizites Verfahren!).
• Die Jacobi-Matrix enthält die Werte der partiellen Ableitungen aller Zustandsgrößen nach allen Zustandsgrößen (=Wechselwirkung zwischen Zustandsgrößen).
• Die Jacobi-Matrix wird erst neu berechnet, wenn dies auf Grund von Genauigkeitskriterien als erforderlich erkannt wird (z.B. mangelnde Konvergenz). Die Berechnung erfolgt in modernen Systemen symbolisch, in älteren noch über Abtastung des Modells.

Auswahl von Integrationsverfahren

In jedem kommerziellen Simulationsprogramm zur Dynamik-Simulation sind mehrere Integrationsverfahren implementiert, welche unterschiedliche Qualitäten besitzen. Der Nutzer sollte für seine konkrete Simulationsaufgabe ein Verfahren wählen, welches:

1. mit möglichst wenigen Stützstellen (Modellberechnungen) den zeitlichen Verlauf der Zustandsgrößen hinreichend genau ermittelt und
2. möglichst unempfindlich auf die Änderungen von Modellparametern reagiert (also stabil rechnet).

• Die Anzahl der erforderlichen Modellberechnungen für ein konkretes Modell wird wesentlich von der maximalen Integrationsschrittweite dt bestimmt, mit welcher ein Verfahren noch stabil rechnet.
• Um Verfahren in Hinblick auf die maximal zulässige Schrittweite dt vergleichen zu können, wird diese in Relation gesetzt zur kleinsten Zeitkonstante T bzw. zur Periodendauer T der höchsten Eigenfrequenz im Dynamikmodell (z.B. C·R, L/R, (L·C)^1/2, (m/c)^1/2 ).
• Zusammen mit der Zahl der Stützstellen pro Integrationsschritt ergibt sich die Anzahl der erforderlichen Modellberechnungen n pro Zeitkonstante bzw. Periodendauer T.
• Ein Kennzeichen für die Stabilität eines Verfahrens ist das Verhalten bei Überschreiten der maximal zulässigen Schrittweite. Günstig ist hierbei, wenn sich die Genauigkeit dabei nur stetig verschlechtert.

Explizite Verfahren
EULER                 : dtmax ≈ T/1000  n ≈ 1000/T (stark aufschaukelnd)
HEUN                  : dtmax ≈ T/10    n ≈   20/T (schwach aufschaukelnd)
Runge-Kutta 4.Ordn.   : dtmax ≈ T/5     n ≈   20/T (dämpfend, dann chaotisch)
Runge-Kutta-Fehlberg* : dtmax ≈ T/3     n ≈   18/T (dämpfend, dann chaotisch)
Implizite Verfahren (zusätzlicher Rechenaufwand für Erstellen der Jacobi-Matrix!)
Weighted Average      : dtmax ≈ T/200   n >  200/T (dämpfend, dann chaotisch)
Rosenbrock-Wanner*    : dtmax ≈ T/3     n >   18/T (stochastisch)
BDF-Verfahren*        : dtmax ≈ T/3     n >   18/T (stochastisch)

• "Weighted Average" ist ein implizites Verfahren, welches mit einem Wichtungsfaktor in seiner Wirkung zwischen EULER- und HEUN-Verfahren eingestellt werden kann.
• Die Verfahren mit geregelter Schrittweite (*) passen ihre aktuelle Schrittweite an die aktuell wirksame Zeitkonstante bzw. Periodendauer T an.
• Auf den ersten Blick unterscheiden sich explizite und implizite Verfahren höherer Ordnung kaum im erforderlichen Berechnungsaufwand. Hier kommt jedoch ein wichtiger Unterschied zwischen beiden Verfahrensklassen zur Wirkung:
  • Die Schrittweite dt eines expliziten Verfahrens richtet sich nur nach der kleinsten Zeitkonstante bzw. höchsten Eigenfrequenz, welche im Modell existiert. Dies gilt auch dann, wenn dieser kleine Wert für T aktuell nicht wirkt, weil z.B. ein harter mechanischer Anschlag aktuell nicht stattfindet! Das Modell muss also während der gesamten Simulationszeit unter Umständen mit extrem kleiner Schrittweite berechnet werden.
  • Durch implizite Verfahren werden Zeitkonstanten und Eigenfrequenzen vernachlässigt, welche im aktuellen Modellverhalten nicht wirksam sind. Diese werden bei der Bildung der Jacobi-Matrix als "lineares Ersatzmodell" nicht berücksichtigt. Damit ist es möglich, steife DGL (mit extrem unterschiedlichen Eigenfrequenzen) überwiegend mit großen Integrationsschrittweiten zu berechnen.
• Ein weiteres Problem sind die algebraischen Schleifen in den DGL, welche aus zusätzlichen Zwangsbedingungen zwischen Zustandsgrößen resultieren (z.B. Bewegungsgrößen in Getrieben):
  • Aus obiger Liste sind dafür nur die BDF-Verfahren geeignet, welche auch als DASSL (Differential Algebraic System Solver) bekannt sind.
  • Algebraische Schleifen sind auf Grund des Modellkonzepts in der Modellierungssprache Modelica die Regel. Deshalb wird bei Modelica-basierten Simulationssystemen meist ein BDF-Verfahren als Standardverfahren vorgegeben und benutzt.

Behandlung von Unstetigkeit als zeitdiskrete Ereignisse

Ereignisse im Simulationslauf

Spricht man von der Stetigkeit eines dynamischen Modells, so meint man damit nur die Stetigkeit der Zustandsgrößen-Funktionen:

• Die Werte der Zustandsvariablen des Modells dürfen in stetigen Modellen zu keinem Zeitpunkt Sprünge machen.
• Die Ableitungen der Zustandsgrößen dürfen in stetigen Modellen jedoch unstetig sein!

Die im Solver implementierten Verfahren der numerischen Integration liefern Lösungen nur innerhalb stetiger Bereiche dynamischer Modelle:

• Die Grenze stetiger Modell-Bereiche ist durch sprunghafte Wertänderung von Zustandsgrößen gekennzeichnet.
• Der Übergang in einen benachbarten stetigen Modell-Bereich muss durch eine sogenannte Ereignisbehandlung erfolgen, welche konsistente Anfangswerte für alle Zustandsgrößen berechnet, nachdem einzelne Zustandsgrößen sprunghaft ihren Wert geändert haben.
• An der Grenze eines neuen stetigen Modell-Bereiches muss ein Neustart der numerischen Integration erfolgen (z.B. Erzeugen der "Historie" bei Mehrschrittverfahren).

Umgangssprachliche Definition von Ereignissen

In der Wikipedia kann man nachlesen, dass Ereignis vom neuhochdeutschen Wort eräugen abstammt:

1. Das Zustandekommen einer bestimmten Konstellation muss als Ereignis definiert (benannt) sein (meist vor dem Ereignis).
2. Es muss zusätzlich ein Beobachter existieren, damit Ereignisse bemerkt ("eräugt") werden.

Als Ereignis wird meist der Augenblick des Zustandekommens der besonderen Umstände gewertet. Es tritt dann zu einem diskreten Zeitpunkt schlagartig ein (keine Zwischenzustände!). Man kann zwei Formen von Ereignissen unterscheiden:

1. Prognostizierbare Ereignisse : Der Ereignis-Zeitpunkt ist durch Beobachtung der sich ändernden Umstände voraussagbar.
2. Zufällige Ereignisse : Wenn sich die Umstände aus Sicht des Beobachters stochastisch ändern, ist der Ereignis-Zeitpunkt erst nach dem Eintritt des Ereignisses bekannt.

Numerische Definition von Ereignissen

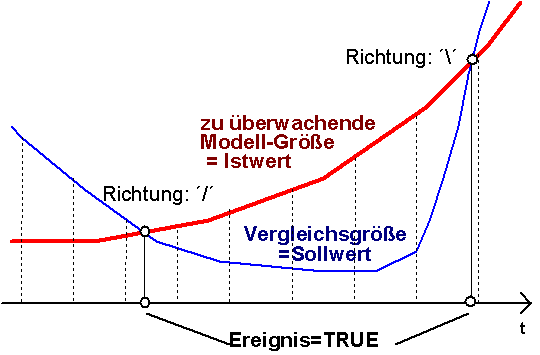
Die Unstetigkeiten eines Dynamik-Modells sind durch konkrete qualitative Merkmale gekennzeichnet (z.B. die Massen kollidieren). Damit solche Unstetigkeiten während der Simulation mit geringem numerischen Aufwand als Ereignisse erkannt werden können, wird die Definition eines Ereignisses auf einen einfachen Zahlenvergleich reduziert:

• Erreichen eines Zustands während des Modellaufes, in dem eine sich zeitlich ändernde Größe den Wert einer Vergleichsgröße annimmt:
  
• Als Beoabachter für jedes definierte Ereignis wird eine sogenannte Zero-Function genutzt. Diese registriert, bewertet und behandelt die Nulldurchgänge der Differenz von Ist- und Sollgröße.
• Zero-Functions werden automatisch für alle unstetigen Funktionen (sign, abs, ...) und für die Testbedingung in Alternativ- und Schleifenanweisungen (if, for, ...) generiert.

Klassifizierung numerischer Ereignisse

Zufällige Ereignisse spielen nur eine Rolle bei der Fehlerbehandlung in Hinblick auf unzulässige Modell-Werte, wenn diese aus dem stochastischem Verhalten des Solvers oder eingespeisten Mess-Signalen resultieren:

• Vermeidung mathematisch nicht definierter Operationen (z.B. Null-Division, negative Wurzel)
• Vermeidung physikalisch-technisch ungültiger Modell-Werte (z.B. negative Masse, negative Kelvin-Absoluttemperatur), negativer Abstand)

Eine Ereignisbehandlung im Sinne der Überwindung von Modell-Unstetigkeiten wird hierfür im Normalfall nicht durchgeführt. Die Maßnahmen werden sich bei der Fehlerbehandlung auf das Setzen zulässiger Modell-Werte bzw. auf den Abbruch der Modellberechnung beschränken.

Bei den in den Dynamik-Modellen definierten Ereignissen handelt es sich überwiegend um prognostizierbare Ereignisse. Deren Ereignis-Zeitpunkt kann auf Grundlage der sich stetig ändernden Modellgrößen über eine begrenzte Zeitspanne hinweg vorausberechnet werden. Es wird dabei unterschieden zwischen zustands- und zeitabhängigen Ereignissen.

Zustandsabhängige Ereignisse:

• werden durch Zerofunctions erkannt (ändern zum Ereigniszeitpunkt ihr Vorzeichen)
• in unstetigen Funktionen (z.B. abs(x), sign(x))und bedingten Anweisungen (z.B. if..then..else)
• Solver versucht, durch Prognose den Zeitpunkt möglichst genau zu treffen
• Die kontinuierliche Integration wird kurz hinter dem tatsächlichen Ereigniszeitpunkt gestoppt (z.B. in SimulationX maximal dtDetect danach).
• Zu diesem prognostizierten Zeitpunkt wird die Ereignisbehandlung gestartet

Zeitabhängige Ereignisse:

• in zeitdiskreten Signalgliedern, z.B.
  • AD-/DA-Wandler
  • Abtast- & Halteglied
  • diskrete Integratoren / Differentierer
  • Z-Übertragungsfunktion
• in Funktionen sample() bzw. delay() zum Setzen von Zeit-Ereignissen bzw. Signal-Verzögerung
• Eintrag von zeitabhängigen Ereignissen in eine Ereigniswarteschlange - der Solver startet exakt zu diesen Zeitpunkten die Ereignisbehandlung

Ereignisbehandlung

Die Ereignisbehandlung soll einen neuen konsistenten Zustand aller Zustandsgrößen nach der Unstetigkeit herstellen:

• Während der Ereignisbehandlung bleibt die Modellzeit konstant (time bzw. t).
• Zu diesen Zeitpunkt wird eine so genannte Ereignis-Iteration durchgeführt.
• Die Werte der elementaren Relationen (true bzw. false) bleiben während der kontinuierlichen Integration konstant, d.h. kurz vor einer Ereignis-Iteration wird noch mit den alten Werten gerechnet, obwohl sich die Relation schon geändert haben kann (Stopp nach dem wirklichen Ereigniszeitpunkt!)
• Während der Ereignis-Iteration ändern die Relationen ihre Werte und danach werden für den gleichen Zeitpunkt neue konsistente Anfangswerte bestimmt. So erhält man zwei Werte eines Werteverlaufs an dem Zeitpunkt der Unstetigkeit: einen vor der Iteration und einen danach.
• Mit einem noEvent-Operator kann man verhindern, dass ausgewählte Relationen Ereignisiterationen auslösen. Das kann man z.B. dazu benutzen, um den Definitionsbereich einer Funktion abzusichern:

y:= if noEvent(x>=0) then sqrt(x) else 0;

• Der noEvent-Operator verhindert im Beispiel die automatische Generierung einer Zerofunction zur Ereignisbehandlung für die Testbedingung (x>=0). Ohne noEvent würde ein Fehler (Wurzel aus neg. Zahl) auftreten, weil kurz vor der Ereignis-Iteration der Wert von x schon negativ wird, obwohl x>=0 noch "true" bleibt.

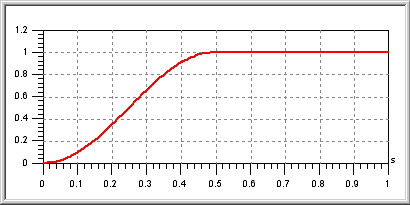
Ein weiteres Beispiel aus der SimulationX-Hilfedatei zur die Vermeidung unerwünschter Ereignisbehandlung:

• Als Sollwertverläufe für Positioniervorgänge werden gern Abschnitte von sin²-Funktionen verwendet:
  
• Ein solches Signal kann man erzeugen mit dem Ausdruck:

if t<=0.5 then sin(pi*t)^2 else 1

• Für die Relation wird automatisch ein Ereignis bei 0.5 s erzeugt, obwohl dort gar keine Unstetigkeit auftritt.
• Der noEvent Operator führt hier zum Ausbleiben des Ereignisses und damit zu einer Beschleunigung der Rechnung, ohne dass damit Genauigkeitseinbußen verbunden sind:

if noEvent(t<=0.5) then sin(pi*t)^2 else 1

Beispiel: Extremwert-Sensor

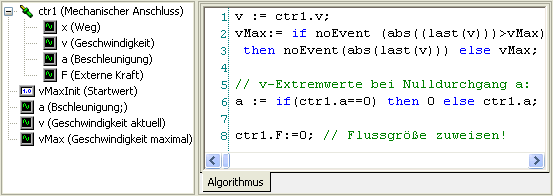
Eine typische Modellierungsaufgabe ist die Erfassung des Extremwert-Betrages einer physikalischen Größe während des Simulationslaufes. Im Beispiel wird in einem SimulationX-Modell die Maximalgeschwindigkeit einer translatorischen Masse erfasst. Das Programmieren der Maximalwert-Erfassung erscheint auf den ersten Blick sehr einfach, wenn man zuvor den Extremwert vMax mit dem Anfangswert=0 versehen hat:

vMax := if abs(v) > vMax then abs(v) else vMax;

Leider gestaltet sich die Einbindung in ein Dynamik-Modell infolge des Wirkens der numerischen Integration und der Ereignisbehandlung ziemlich kompliziert:

• Vor der Dynamik-Berechnung im Zeitbereich muss die Extremwert-Variable vMax einen sinnvollen Startwert erhalten (vMaxInit als Anfangswert von vMax).
• Man muss gewährleisten, dass die "irreversible" Aktualisierung der aktuellen Extremwerte nur auf Basis "gültiger" Modellwerte erfolgt (last-Function):
  

Erläuterung:

• Die Verwendung unstetiger Funktionen sollte nicht zu unnötigen Ereignisbehandlungen führen (noEvent-Operator).
• Entnimmt man die zu überwachende Größe einem energetischen Konnektor, so muss man zur Vermeidung undefinierter Rückwirkungen die Flussgröße auf Null setzen (ctr1.F:=0):
• Tritt der Extremwert nicht an einer bereits behandelten Unstetigkeitsstelle auf, so muss gezielt eine solche Testbedingung installiert werden! Nur so wird auch der Extremwert-Zeitpunkt berechnet (z.B. Nulldurchgang von a).
• Infolge der Optimierung des Gleichungssystems vor der Simulation kann es passieren, dass in späteren Programm-Versionen solche zusätzlichen Test-Bedingungen "wegoptimiert" werden!
• Sensor-Elemente von Modellbibliotheken liefern nicht nur "gültige" Signale. Das muss man ebenfalls durch Anwendung der last-Function berücksichtigen.

An diesem Beispiel sollte deutlich werden, dass die Berücksichtigung der Ereignisbehandlung bei der Modellbildung nicht einfach ist. Das Funktionieren von Tricks zur exakten Erfassung des Ereigniszeitpunkten ist stark abhängig vom "Optimierungspotential" des aktuell verwendeten Solvers.

Lineare und nichtlineare Systeme

Modellcharakter von Systemen

Der Begriff "System" wird inflationär mit verschiedenen Zusätzen benutzt, z.B.:

• lineares bzw. nichtlineares System
• chaotisches System
• offenes, geschlossenes, abgeschlossenes System
• emergentes System

Dies führt nicht unbedingt zu einem besseren Verständnis für das Wesen des Begriffs "System". Deshalb hier die Zusammenfassung der wesentlichen Merkmale, die man einem System zuordnet:

• besitzt eine Abgrenzung zu seiner Umgebung;
• enthält Komponenten, die Wirkung aufeinander auswirken;
• es entsteht ein Systemverhalten, welches eine neue Qualität im Vergleich zu den Elementen aufweist (z.B. Spule und Kondensator ergibt einen Schwingkreis);
• die resultierenden Systemgesetze engen den Freiheitsgrad der Komponenten ein! (Versklavung der Komponenten durch Abhängigkeiten).

Man muss unterscheiden zwischen

• dem physikalischen System (real existierendes physikalisches Objekt) und
• dem System-Konstrukt, welches als idealisiertes, vereinfachtes Abbild im Betrachter des physikalischen Systems entsteht.

Das System-Konstrukt ist somit ein Modell zum Verstehen eines als "System" betrachteten komplexen Gebildes.

Dynamische Systeme

Unter einem dynamischen System versteht man das mathematische Modell eines zeitabhängigen Prozesses, dessen Verlauf vom Anfangszustand abhängt:

• Das System enthält Speicherelemente, d.h. es existiert ein Vektor von kontinuierlichen bzw. diskreten Zustandsgrößen Y(t).
• Es gibt eine Überführungsfunktion T (=dynamisches Modell des Systems), welche die Änderung der Zustandsgrößen in einem Zeitintervall Δt beschreibt:

mit

• Der Eingangsvektor u(τ) repräsentiert externe Signale, welche in das System eingespeist werden.

Man kann folgende Sonderformen von dynamischen Systemen unterscheiden:

• deterministisches System: die Überführungsfunktion T ist eindeutig
• stochastisches System: die Überführungsfunktion T ist mehrdeutig (Wahrscheinlichkeitsverteilung für das Erreichen der folgenden Zustände).
• autonomes System: die Überführungsfunktion T ist unabhängig von der aktuellen Systemzeit t (d.h., das System entwickelt sich unabhängig vom Startzeitpunkt t₀).

Beispiele:

• Ein Feder-Masse-Schwinger lässt sich als kontinuierliches, deterministisches und autonomes System beschreiben mit einer gewöhnlichen DGL beschrieben.
• Biotope lassen sich als autonome, stochastische Systeme beschreiben (Übergangswahrscheinlichkeiten zwischen zeitlich aufeinanderfolgende Zustände).

Wann kann man ein System als lineares System behandeln

• Für die Behandlung linearer Systeme existiert ein umfangreiches mathematisches Methoden-Inventar.
• Das Verhalten linearer Systeme kann analytisch durch Anwendung der entsprechenden mathematischen Verfahren auf der Basis linearer Gleichungssysteme berechnet werden.

Beispiel "Theorie der Wechselstromschaltung":
Wenn die Schaltelemente konstante Parameter R, L, C besitzen und die Schaltung mit Sinusspannung gespeist wird, kann man durch Transformation der Differentialgleichung in den Bildbereich der komplexen Zahlen lineare Gleichungssysteme aufstellen und lösen.

Verallgemeinert gilt:
Sind Speicher- und Übertragungselemente konstant, so kann man Transformationen in einen Bildbereich durchführen, wenn sich der Eingangsvektor u(t) des Systems auf ein Spektrum harmonischer Schwingungen zurückführen lässt:

• Sinus ⇒ Bildbereich der komplexen Zahlen,
• Sprungfunktion und DIRAC-Impuls ⇒ Laplace-Transformation,
• beliebige periodische Vorgänge ⇒ (Z-Transformation.

Wann muss man ein System als nichtlineares System behandeln

Wenn eines der folgenden drei Kriterien zutrifft, kann man ein System nicht mehr mit den Verfahren für lineare Systeme im Bildbereich berechnen:

1. Das System enthält speichernde Komponenten, deren Fassungsvermögen nicht konstant ist (z.B. Drehträgheit bei Eiskunstlauf-Pirouette)
   oder
   
2. Das System enthält Übertragungselemente zwischen den Speichern, deren Übertragungsfunktion abhängig ist vom aktuellen Wert der übertragenen Größe (durch sich ändernde Werkstoffeigenschaften)
   oder
   
3. Der Eingangsvektor u(t) ist aus Sicht des Systems zufällig.

Eine Transformation in einen Bildbereich und die analytische Lösung von linearen Gleichungssystemen ist dann nicht mehr möglich. In der Simulationspraxis hat dies im Normalfall nur geringe Bedeutung:

• DGL beschreiben den Fluss von Energie, Stoff oder Information zwischen den Speicherkomponenten zeitkontinuierlicher dynamischer Systeme.
• Auch für nichtlineare Systeme ist das Aufstellen der DGL meist einfach. Nur ihre analytische Lösung ist äußerst schwierig bis unmöglich.
• "Zum Glück" können diese nichtlinearen dynamischen Modelle numerisch mit geeigneten Simulationssystemen genauso einfach berechnet werden. Allerdings sind dabei einige Besonderheiten zu beachten, welche im nächsten Abschnitt beschrieben werden.
• Nur für Anwendungsfälle, in denen kurze Berechnungszeiten oberste Priorität besitzen, spielt die Möglichkeit der linearen Berechnung in einem Bildbereich zurzeit noch eine Rolle (z.B. bei Echtzeitfähigkeit von Modellen).

Numerische Stabilisierung unstetiger nichtlinearer Elemente

Die Verfahren der numerischen Integration funktionieren stabil auch für nichtlineare Systeme, wenn im zu berechnenden Modell alle erforderlichen zeitlichen Ableitungen der Zustandsgrößen einen stetigen Verlauf besitzen. Ein stetiger Verlauf (ohne Sprünge bzw. Polstellen) ist meist gewährleistet:

• bei analytischer Formulierung der Zusammenhänge (z.B. physikalischer Effekte) ohne diskretisierende Operationen (wie Rundung, Vorzeichen, Fallunterscheidung) und ohne mögliche Divisionen durch Null (z.B. an Polstellen trigonometrischer Funktionen).
• bei der Interpolation zwischen Stützstellen von Übertragungsfunktionen, welche nur in abgetasteter Form vorliegen (z.B. im Ergebnis von Messungen oder FEM-Simulationen), in Form von Polynomen oder Splines.

Unstetigkeiten in den Ableitungen führen meist zu Ereignisbehandlungen, welche den Simulationsfortschritt zumindest "ausbremsen" und bei Polstellen (Wert → ∞) meist zum abnormalen Abbruch der Simulation führen. Für einige in numerischer Hinsicht problematische Modell-Elemente werden im Folgenden Lösungen vorgeschlagen, wie Unstetigkeiten durch stetige Funktionen nachgebildet werden können, welche eine numerisch stabile Simulation ermöglichen.

Nichtlineare Energiespeicher

• Das idealisierte, konzentrierte Element eines Energiespeichers wird beschrieben durch einen Parameterwert p (z.B. m, C, L).
• Dieser Parameter beschreibt vereinfacht, wie "träge" sich die Zustandsgröße ändert, wenn Energie zugeführt oder entzogen wird.
• Für den Fall konstanter Speicherelemente (p=konstant) ergeben sich die bekannten einfachen Berechnungen der Zustandsgrößen:

1. Translatorische Bewegung einer Masse:
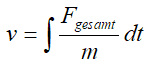
2. Rotatorische Bewegung einer Drehträgheit:
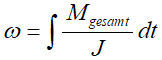
3. Strom durch Induktivität einer Spule:
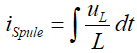
4. Spannung einer elektrischen Kapazität:

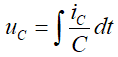
• Diese Zustandsgleichungen resultieren aus der sinngemäßen Anwendung des Impulssatzes der klassischen Mechanik auf die unterschiedlichen physikalischen Partialsysteme:

1. Kraft verknüpft mit Impulsänderung:
2. Moment verknüpft mit Drehimpulsänderung:
3. induzierte Spannung verknüpft mit Induktionsflußänderung:
4. Strom in Kapazität verknüpft mit Ladungsänderung:

===>>> Abschnitt wird zurzeit erarbeitet !!!!