Grundlagen: Optimierungsverfahren: Unterschied zwischen den Versionen
K (→Zielstellung) |
|||
| Zeile 6: | Zeile 6: | ||
Die Zielstellung für globale Suchverfahren der Optimierung besteht darin, innerhalb eines vorgegebenen Suchraums den absoluten Extremwert (das globale Optimum) zu finden. Bei der Anwendung innerhalb eines Entwurfsprozesses entspricht dies der absolut besten Lösung. D.h., es existiert keine Lösung, welche der idealen Lösung näher kommt: | Die Zielstellung für globale Suchverfahren der Optimierung besteht darin, innerhalb eines vorgegebenen Suchraums den absoluten Extremwert (das globale Optimum) zu finden. Bei der Anwendung innerhalb eines Entwurfsprozesses entspricht dies der absolut besten Lösung. D.h., es existiert keine Lösung, welche der idealen Lösung näher kommt: | ||
* Leider gibt es keine mathematischen oder numerischen Methoden, welche für Suchräume mit mehr als 2-3 Entwurfsparametern das Finden der absolut besten Lösung garantieren können. Findet man einen Extremwert auf Gütefunktion, so weiß man praktisch nie, ob es nicht doch noch eine bessere Lösung gibt. | * Leider gibt es keine mathematischen oder numerischen [http://de.wikipedia.org/wiki/Optimierung_(Mathematik)#Methoden_der_globalen_nichtlinearen_Optimierung Methoden], welche für Suchräume mit mehr als 2-3 Entwurfsparametern das Finden der absolut besten Lösung garantieren können. Findet man einen Extremwert auf Gütefunktion, so weiß man praktisch nie, ob es nicht doch noch eine bessere Lösung gibt. | ||
* Deshalb setzt man globale Suchverfahren innerhalb von Entwurfsprozessen meist "nur" zu Analysezwecken ein. Man verschafft sich damit einen "Überblick" über die Zielfunktion im einen zuvor definierten Suchraum: | * Deshalb setzt man globale Suchverfahren innerhalb von Entwurfsprozessen meist "nur" zu Analysezwecken ein. Man verschafft sich damit einen "Überblick" über die Zielfunktion im einen zuvor definierten Suchraum: | ||
** Innerhalb des Suchraums wird die Oberfläche der Zielfunktion in Form einzelner Abtastpunkte berechnet. | ** Innerhalb des Suchraums wird die Oberfläche der Zielfunktion in Form einzelner Abtastpunkte berechnet. | ||
| Zeile 20: | Zeile 20: | ||
* Der menschliche Blick auf mehrdimensionale Räume sehr eingeschränkt. So versagt bei mehr als 2 Entwurfsparametern recht schnell unsere Vorstellung. | * Der menschliche Blick auf mehrdimensionale Räume sehr eingeschränkt. So versagt bei mehr als 2 Entwurfsparametern recht schnell unsere Vorstellung. | ||
* Man kann immer nur endlich viele ausgewählte Punkte des Suchraums berechnen und muss die Zielfunktion dann hinein interpolieren. Sind die Abstände zwischen den Punkten zu groß, gehen die Details dazwischen natürlich verloren. | * Man kann immer nur endlich viele ausgewählte Punkte des Suchraums berechnen und muss die Zielfunktion dann hinein interpolieren. Sind die Abstände zwischen den Punkten zu groß, gehen die Details dazwischen natürlich verloren. | ||
=== Systematische Suche (Rastersuche) === | |||
Die N Achsen der Entwurfsparameter werden innerhalb des Suchraums in gleichmäßige Abstände geteilt. Die Schnittpunkte der Rasterlinien definieren die Abtastpunkte auf der Oberfläche der Zielfunktion. | |||
In der [http://de.wikipedia.org/wiki/Statistische_Versuchsplanung statistischen Versuchsplanung] ist dieses Verfahren auch als [http://de.wikipedia.org/wiki/Vollständiger_Versuchsplan vollständiger Versuchsplan] (''full factorial design'') bekannt: | |||
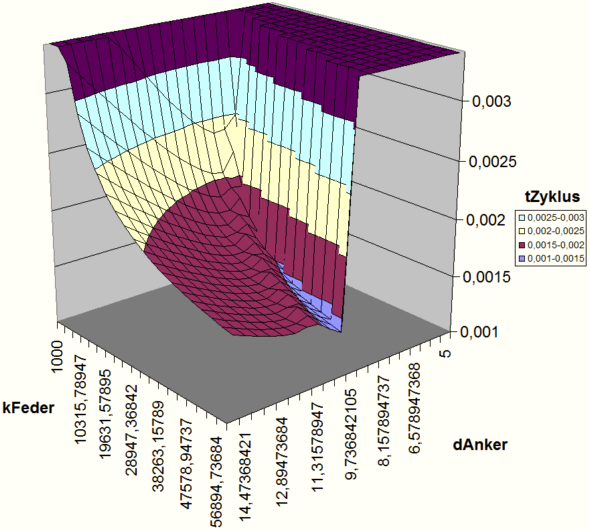
<div align="center"> [[Datei:Grundlagen_Optimierung_Rastersuche_Excel-Darstellung.gif|.]] </div> | |||
* Im obigen Beispiel wurde für einen Elektromagneten die Zykluszeit in Abhängigkeit vom Ankerdurchmesser und der Rückholfeder untersucht. | |||
* Das Verfahren der Rastersuche wird meist als Analyse-Werkzeug für die Eigenschaften einer Zielfunktion benutzt, um die Grundlage für den Einsatz lokaler Suchverfahren zu schaffen. | |||
* Verfügt man über ein hinreichend schnell rechnendes Modell in einem kleinen Suchraum, kann man mit der Rastersuche natürlich auch iterativ recht schnell das mögliche Gebiet des globalen Optimums eingrenzen und dort sogar die exakte Position der bestmöglichen Lösung ermitteln. In obigem Beispiel müsste man den Suchraum zu höheren Federkonstanten verschieben, um das globale Optimum zu umfassen. | |||
Version vom 3. Februar 2014, 09:36 Uhr
Globale Suchverfahren
Zielstellung
Die Zielstellung für globale Suchverfahren der Optimierung besteht darin, innerhalb eines vorgegebenen Suchraums den absoluten Extremwert (das globale Optimum) zu finden. Bei der Anwendung innerhalb eines Entwurfsprozesses entspricht dies der absolut besten Lösung. D.h., es existiert keine Lösung, welche der idealen Lösung näher kommt:
- Leider gibt es keine mathematischen oder numerischen Methoden, welche für Suchräume mit mehr als 2-3 Entwurfsparametern das Finden der absolut besten Lösung garantieren können. Findet man einen Extremwert auf Gütefunktion, so weiß man praktisch nie, ob es nicht doch noch eine bessere Lösung gibt.
- Deshalb setzt man globale Suchverfahren innerhalb von Entwurfsprozessen meist "nur" zu Analysezwecken ein. Man verschafft sich damit einen "Überblick" über die Zielfunktion im einen zuvor definierten Suchraum:
- Innerhalb des Suchraums wird die Oberfläche der Zielfunktion in Form einzelner Abtastpunkte berechnet.
- Man sollte versuchen, daraus die Eigenschaften der Zielfunktion zu erkennen:
- Vorhandensein lokaler Optima, Unstetigkeitsstellen,
- mögliche Position des globalen Optimums,
- sinnvolle Veränderung der Suchraums (Grenzen der Entwurfsparameter verschieben, erweitern oder einengen).
- sinnvolle Positionen von Startpunkten für lokale Suchverfahren.
- Ziel dieser Analyse ist das Ermitteln geeigneter Startpunkte für lokale Suchverfahren in einem sinnvoll definierten Suchraum.
Bei der globalen Analyse der Zielfunktion hat man mit diversen Problemen zu kämpfen:
- Der menschliche Blick auf mehrdimensionale Räume sehr eingeschränkt. So versagt bei mehr als 2 Entwurfsparametern recht schnell unsere Vorstellung.
- Man kann immer nur endlich viele ausgewählte Punkte des Suchraums berechnen und muss die Zielfunktion dann hinein interpolieren. Sind die Abstände zwischen den Punkten zu groß, gehen die Details dazwischen natürlich verloren.
Systematische Suche (Rastersuche)
Die N Achsen der Entwurfsparameter werden innerhalb des Suchraums in gleichmäßige Abstände geteilt. Die Schnittpunkte der Rasterlinien definieren die Abtastpunkte auf der Oberfläche der Zielfunktion.
In der statistischen Versuchsplanung ist dieses Verfahren auch als vollständiger Versuchsplan (full factorial design) bekannt:
- Im obigen Beispiel wurde für einen Elektromagneten die Zykluszeit in Abhängigkeit vom Ankerdurchmesser und der Rückholfeder untersucht.
- Das Verfahren der Rastersuche wird meist als Analyse-Werkzeug für die Eigenschaften einer Zielfunktion benutzt, um die Grundlage für den Einsatz lokaler Suchverfahren zu schaffen.
- Verfügt man über ein hinreichend schnell rechnendes Modell in einem kleinen Suchraum, kann man mit der Rastersuche natürlich auch iterativ recht schnell das mögliche Gebiet des globalen Optimums eingrenzen und dort sogar die exakte Position der bestmöglichen Lösung ermitteln. In obigem Beispiel müsste man den Suchraum zu höheren Federkonstanten verschieben, um das globale Optimum zu umfassen.
Vorläufige Gliederung:
Globale Suchverfahren
- :
- Systematische Suche (Rastersuche)
- Restriktionsbehandlung der systematischen Suche
- Hinweise zur systematischen Suche
- Abtastung der Monte-Carlo-Suche
Lokale Suchverfahren
- Prinzip und Einsatzbereich
- Abtastung und Schrittweitenregelung (am Beispiel "Hooke-Jeeves-Verfahren")
Optimierung nach biologischem Vorbild
- Einführung
- Genetische Algorithmen und Evolutionsstrategie
- Grundlagen zur Evolutionsstrategie
- Konfiguration von Evolutionsstrategien
- Co-Evolutionäre Strategien