Software: OptiY-Workflow - Einfache Toleranzkette

Autoren: Dr.-Ing. PD Thomas Nagel, Dr.-Ing. Alfred Kamusella

Dieser Beitrag wird gerade erstellt und ist noch unvollständig!

Aufgabenstellung

Am Beispiel einer einfachen Maßkette soll gezeigt werden, welche neuen Möglichkeiten die probabilistische Simulation im Vergleich zu klassischen, analytischen Methoden eröffnet:

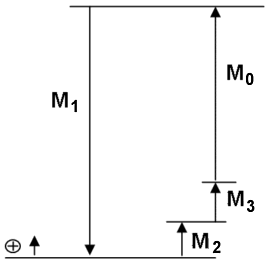
Das Schlussmaß M₀ ergibt sich aus der Gesamt-Abmessung M₁ abzüglich der Teilmaße M₂ und M₃.

Vorgegeben:

• als Ausgangslösung stehen folgende Maße in der Maßkette:
  • M₁= 11,8-0,2
  • M₂= 1,3-0,1
  • M₃= 1,5±0,05
• diese Ausgangslösung besitzt also die Toleranzmittenmaße C_i mit den Toleranzen T_i:
  • C₁=11,70 mit T₁=0,2
  • C₂=  1,25 mit T₂=0,1
  • C₃=  1,50 mit T₃=0,1

Gesucht:

• das Nennmaß des Schlussmaßes N₀
• Toleranzmittenabmaß des Schlussmaßes E_c0
• Toleranz T₀ des Schlussmaßes
• eine Aussage, ob mit der ermittelten Toleranz T₀ die geforderte Toleranz T_{0_Max} des Schlussmaßes eingehalten wird
• günstigere Toleranzen für die Maßglieder der Toleranzkette, um die zulässige Toleranz des Schlussmaßes eventuell voll auszuschöpfen oder die Fertigung kostengünstiger zu gestalten.

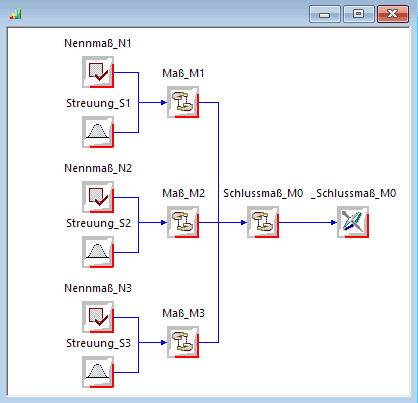
Workflow-Modell der Maßkette

Nach dem Start von OptiY erscheint ein leerer Workflow, den wir nun nutzen, um darauf das Modell der Maßkette zu beschreiben. Dafür einleitend einige Erläuterungen zur Abbildung der toleranzbehafteten Maße auf die Entwurfsparameter (Nennwerte und Streuungen) von OptiY:

• Der zu einer OptiY-Streuung zugeordnete OptiY-Nennwert entspricht dem Toleranz-Mittenmaß C in der Begriffswelt der Maße. Man muss also beachten, dass ein OptiY-Nennwert nicht einem Nennmaß N_i innerhalb der Maßkette entspricht!
• Die OptiY-Streuung Toleranz entspricht dem Wert der Maß-Toleranz T um das Toleranz-Mittenmaß.
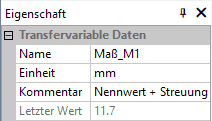
• Der aktuelle Wert eines Maßes M_i ist also immer die Summe aus dem Toleranzmittenmaß C_i und dem Istwert der Abweichung innerhalb der Streuung. Das wollen wir für jedes unserer drei Maße im Workflow beschreiben. Die Bedienung des Workflow-Editor wird in diesem Beispiel vorausgesetzt:

Im Beispiel werden alle Workflow-Elemente mit ausführlichen Bezeichnern versehen. Für den erfahrenen Nutzer genügen später auch die Kürzel Ci, Ti und Mi. Die einzelnen Größen sind immer ausführlich zu kommentieren und mit der richtigen Maßeinheit zu versehen.

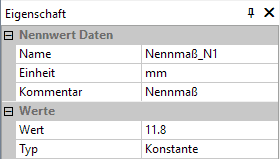
• Toleranzmittenmaße (als Entwurfsparameter - Nennwerte):
  
  • Für die Toleranz-Analyse (Probabilistische Simulation einer Stichprobe) werden die Toleranzmittenmaße als Konstante angenommen.
  • Die aktuellen Istwerte des zugehörigen Maßes streut dann um diesen konstanten Wert.
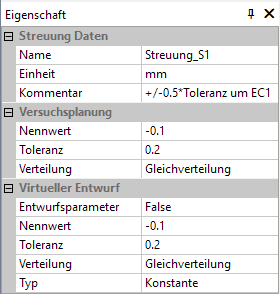
• Toleranzen (als Entwurfsparameter - Streuungen):
  
  • Für die Toleranz-Analyse (Probabilistische Simulation einer Stichprobe) werden die Toleranzen als vorgegebene Konstante angenommen.
  • In Vorbereitung auf die Nachbildung der Maximum-Minimum-Methode wurde eine Gleichverteilung für den aktuellen Maßwert angenommen.
• unabhängige Maße (als Transfervariablen):
  
  • Transfer-Variablen bieten die Möglichkeit, ihren Wert über eine Formel zu berechnen.
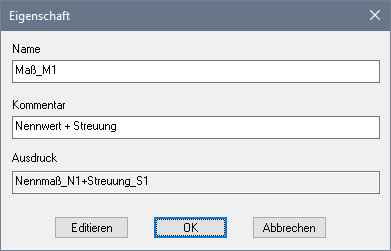
  • Der aktuelle Ist-Wert eines jeden unabhängigen Maßes Mi berechnet man aus der Summe von Toleranzmittenmaß Ci und aktueller Maßabweichung im Rahmen des Toleranzbereiches Ti:
    
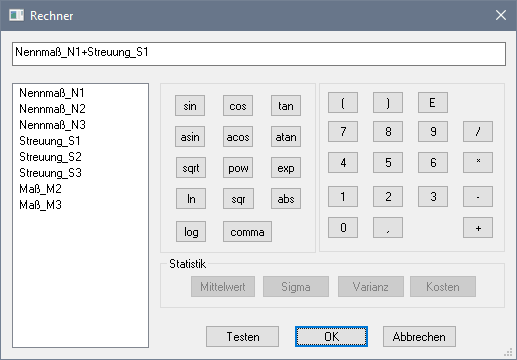
  • Den erforderlichen Formel-Ausdruck bearbeitet man im OptiY-Workflow mit dem Rechner:
    
• Schlussmaß (als Restriktion):
  Datei:Software OptiY-Workflow - Einfache Toleranzkette eigenschaft schlussmass.gif
  • Unter- und Obergrenze der Restriktionsgröße beschreiben den zulässigen Bereich für dieses Schlussmaß. Solange dafür noch keine Werte bekannt sind, sollte man die Grenzen so weit setzen, dass auftretende Werte des Schlussmaßes in jedem Fall zulässig sind (im Beispiel 0 bis 1 Meter).
  • Der Wert des Gewichtsfaktors hat vorläufig keine Bedeutung und sollte den Standardwert=1 behalten
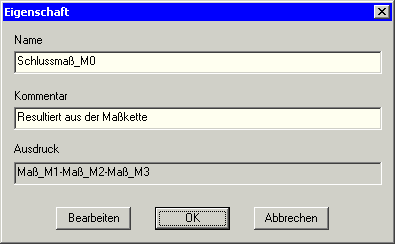
  • Das Schlussmaß M0 wird über einen Formel-Ausdruck aus allen unabhängigen Maßen Mi berechnet:
    
  • Zum Bearbeiten dieses Ausdrucks benutzt man wieder den Rechner.

Maximum-Minimum-Methode

Diese Methode berücksichtigt bei der Berechnung der Schlussmaß-Toleranz die Worst-Case-Fälle und gewährleistet damit eine 100%-ige Einhaltung des Schlussmaßes.

Die klassische Maximum-Minimum-Methode berechnet folgende Größen des Schlussmaßes:

• das Nennmaß N₀ aus den unabhängigen Nennmaßen N_i
  • N₀ = -1 • (1,5 + 1,3 - 11,8) = 9,0
• das Toleranzmittenabmaß E_c0 aus den unabhängigen Toleranzmittenabmaßen E_ci
  • E_c0 = -1 • (0 - 0,05 + 0,1) = -0,05
• die Toleranz T₀ ergibt sich infolge der linearen Kette aus der Summe der Einzeltoleranzen T_i
  • T₀=0,2+0,1+0.1=0,4
• Damit ergibt sich das Schlussmaß M₀=8,95±0,2

Zum gleichen Ergebnis gelangt man mit der probabilistischen Simulation der Maßkette, wenn man jedes unabhängige Maß als gleichverteilt betrachtet.