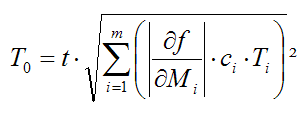Software: OptiY-Workflow - Einfache Toleranzkette: Unterschied zwischen den Versionen
| Zeile 6: | Zeile 6: | ||
<div align="center">[[Bild:Software_OptiY-Workflow_-_Einfache_Toleranzkette_anordnung.gif]]</div> | <div align="center">[[Bild:Software_OptiY-Workflow_-_Einfache_Toleranzkette_anordnung.gif]]</div> | ||
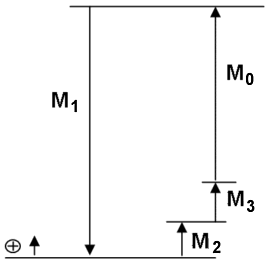
Das Schlussmaß '''M<sub>0</sub>''' ergibt sich aus der Gesamt-Abmessung '''M<sub>1</sub>''' abzüglich der Teilmaße '''M<sub>2</sub>''' und '''M<sub>3</sub>'''. | Das Schlussmaß '''M<sub>0</sub>''' ergibt sich aus der Gesamt-Abmessung '''M<sub>1</sub>''' abzüglich der Teilmaße '''M<sub>2</sub>''' und '''M<sub>3</sub>'''. | ||
'''Vorgegeben:''' | '''Vorgegeben:''' | ||
Version vom 20. Oktober 2016, 07:22 Uhr
Aufgabenstellung
Am Beispiel einer einfachen Maßkette soll gezeigt werden, welche neuen Möglichkeiten die probabilistische Simulation im Vergleich zu klassischen, analytischen Methoden eröffnet:
Das Schlussmaß M0 ergibt sich aus der Gesamt-Abmessung M1 abzüglich der Teilmaße M2 und M3.
Vorgegeben:
- als Ausgangslösung stehen folgende Maße in der Maßkette:
- M1= 11,8-0,2
- M2= 1,3-0,1
- M3= 1,5±0,05
- diese Ausgangslösung besitzt also die Toleranzmittenmaße Ci mit den Toleranzen Ti:
- C1=11,70 mit T1=0,2
- C2= 1,25 mit T2=0,1
- C3= 1,50 mit T3=0,1
- Die Nennwerte N1 und Toleranzmittenabmaße Eci der Ausgangslösung betragen somit:
- N1= 11,8 mit Ec1= -0,1
- N2= 1,3 mit Ec2= -0,05
- N3= 1,5 mit Ec3= 0
Gesucht:
- das Nennmaß des Schlussmaßes N0
- Toleranzmittenabmaß des Schlussmaßes Ec0
- Toleranz T0 des Schlussmaßes
- eine Aussage, ob mit der ermittelten Toleranz T0 die geforderte Toleranz T0_Max des Schlussmaßes eingehalten wird
- günstigere Toleranzen für die Maßglieder der Toleranzkette, um die zulässige Toleranz des Schlussmaßes eventuell voll auszuschöpfen oder die Fertigung kostengünstiger zu gestalten.
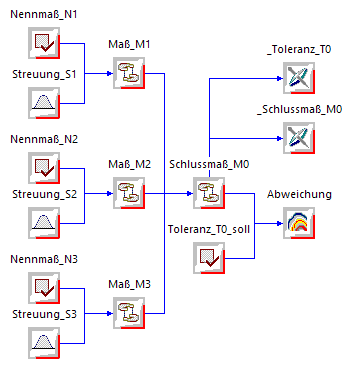
Workflow-Modell der Maßkette
Nach dem Start von OptiY erscheint ein leerer Workflow, den wir nun nutzen, um darauf das Modell der Maßkette zu beschreiben. Dafür einleitend einige Erläuterungen zur Abbildung der toleranzbehafteten Maße auf die Entwurfsparameter (Nennwerte und Streuungen) von OptiY:
- Die Nennwerte des OptiY-Workflow entsprechen den Nennmaßen Ni.
- Die Streuungen enthalten die Toleranzmittenabmaße Eci und die Toleranzbreiten Ti.
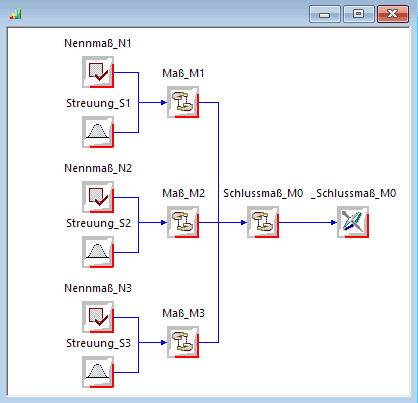
- Der aktuelle Wert eines Maßes Mi entspricht der Summe aus dem Nennmaß Ni und dem Istwert der Abweichung innerhalb der Streuung Si. Das wollen wir für jedes unserer drei Maße mit dem folgenden Workflow beschreiben. Die Bedienung des Workflow-Editor wird in diesem Beispiel vorausgesetzt:
Im Beispiel werden alle Workflow-Elemente mit ausführlichen Bezeichnern versehen. Für den erfahrenen Nutzer genügen später auch die Kürzel Ni, Ti und Mi. Die einzelnen Größen sind immer ausführlich zu kommentieren und mit der richtigen Maßeinheit zu versehen.
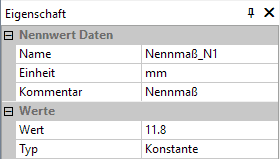
- Nennmaße (als Entwurfsparameter - Nennwerte):
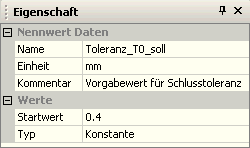
- Für die Toleranz-Analyse (Probabilistische Simulation einer Stichprobe) werden die Toleranzmittenmaße als Konstante angenommen.
- Die aktuellen Istwerte des zugehörigen Maßes streuen dann in Bezug auf diesen konstanten Wert.
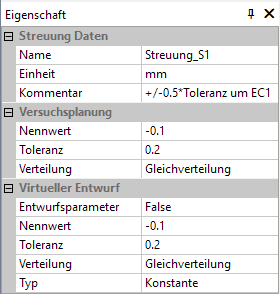
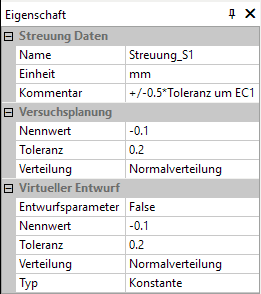
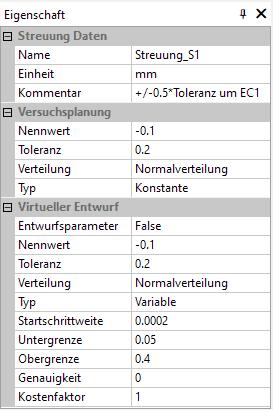
- Streuungen (als Entwurfsparameter - Streuungen):
- Eine Streuung wird beschrieben durch das Toleranzmittenabmaß Eci und die dazu symmetrische Toleranz Ti.
- Der Begriff Nennwert als Parameter der Streuung ist im OptiY ungünstig gewählt. Im OptiY handelt sich hier um das Toleranzmittenabmaß Eci als algebraische Differenz zwischen dem Toleranzmittenmaß und dem Nennmaß.
- In Vorbereitung auf die Nachbildung der Maximum-Minimum-Methode wurde eine Gleichverteilung für den aktuellen Maßwert angenommen.
- Für die Toleranz-Analyse (Probabilistische Simulation einer Stichprobe) werden die Toleranzen als vorgegebene Konstante angenommen.
- Die Bedeutung der Parameter des virtuellen Entwurfs wird später bei der Durchführung der Analyse-Experimente erläutert.
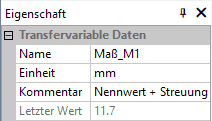
- unabhängige Maße (als Transfervariablen):
- Transfer-Variablen bieten die Möglichkeit, ihren Wert über eine Formel zu berechnen.
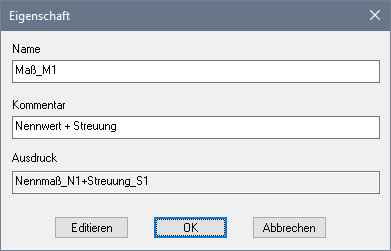
- Im Beispiel wird das genutzt, um den aktuellen Ist-Wert eines jeden unabhängigen Maßes Mi aus der Summe von Nennwert Ni und aktueller Maßabweichung im Rahmen des Streubereiches Eci+Ti zu berechnen:
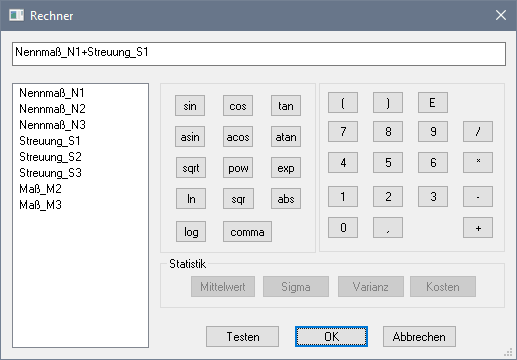
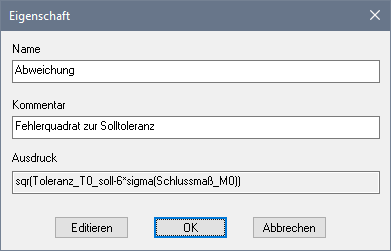
- Den erforderlichen Formel-Ausdruck editiert man im OptiY-Workflow mit dem Rechner:
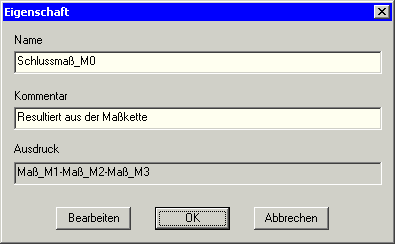
- Schlussmaß (als Transfervariable und als "unwirksame" Restriktion):
- Normalerweise definiert man Ergebnisgrößen innerhalb des OptiY-Workflows nur als Restriktionen oder Gütekriterien. Da im Rahmen einer angestrebten Toleranzoptimierung das Schlussmaß M0 noch für die Formulierung von Gütekriterien benötigt wird, muss man für die Berechnung von M0 eine Transfervariable benutzen. Restriktionen und Gütekriterien können leider in Formel-Ausdrücken anderer Workflow-Elemente nicht verwendet werden!
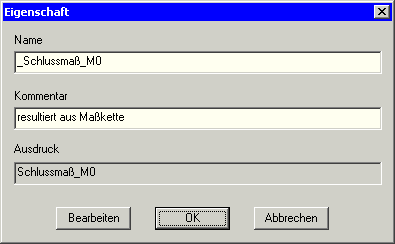
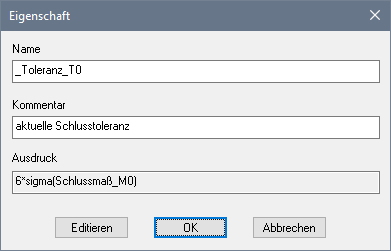
- Das Schlussmaß M0 wird über einen Formel-Ausdruck aus allen unabhängigen Maßen Mi berechnet. Zum Editieren dieses Ausdrucks benutzt man wieder den Rechner:
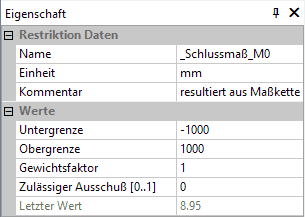
- Damit man die Streuung des Schlussmaßes M0 analysieren kann, muss man M0 zusätzlich einer Restriktionsgröße zuweisen. Wir ergänzen deshalb unseren Workflow noch um eine Restriktionsgröße _Schlussmaß_M0. Die Zuweisung des Wertes dieser Restriktionsgröße erfolgt über den Formel-Ausdruck aus der Transfervariablen "Schlussmaß_M0":
- Wir benötigen die Restriktionsgröße _Schlussmaß_M0 nur als Ergebnisgröße für das Schlussmaß. Deshalb setzt man die Grenzen weit außerhalb möglicher Werte, damit diese Restriktion nicht wirkt:
Maximum-Minimum-Methode
Diese Methode berücksichtigt bei der Berechnung der Schlussmaß-Toleranz die Worst-Case-Fälle und gewährleistet damit eine 100%-ige Einhaltung des Schlussmaßes.
Die klassische Maximum-Minimum-Methode berechnet folgende Größen des Schlussmaßes:
- das Nennmaß N0 aus den unabhängigen Nennmaßen Ni
- N0 = -1 • (1,5 + 1,3 - 11,8) = 9,0
- das Toleranzmittenabmaß Ec0 aus den unabhängigen Toleranzmittenabmaßen Eci
- Ec0 = -1 • (0 - 0,05 + 0,1) = -0,05
- die Toleranz T0 ergibt sich infolge der linearen Kette aus der Summe der Einzeltoleranzen Ti
- T0=0,2+0,1+0.1=0,4
- Damit ergibt sich das Schlussmaß M0=8,95±0,2
Zum gleichen Ergebnis gelangt man mit der probabilistischen Simulation der Maßkette, wenn man jedes unabhängige Maß als gleichverteilt betrachtet. Die Elemente der Maßkette wurden beim Aufbau des OptiY-Workflows bereits richtig konfiguriert.
Die probabilistische Simulation der Maßkette ín Anlehnung an die Maximum-Minimum-Methode soll nun das erste Experiment sein, welches wir mit dem Workflow-Modell durchführen:
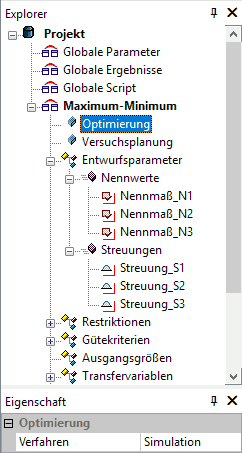
- Wir werden noch mehrere Experimente in diesem OptiY-Versuchsstand durchführen. Deshalb sollte man über das Kontextmenü (Rechter Mausklick) das Experiment Umbenennen in Maximum-Minimum.
- Als "Optimierungsverfahren" wählen wir die "Simulation".
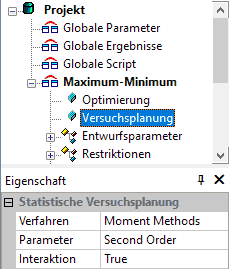
- Nach welchem Verfahren die probabilistische Simulation durchgeführt wird, konfiguriert man in der statistischen Versuchsplanung:
- Für den einfachen linearen Zusammenhang ist eine Moment-Methode das genaueste und effizienteste Verfahren.
- Es soll vorläufig als Ersatzfunktion M0=f(T1,T2,T3) eine Taylorreihe zweiter Ordnung genutzt werden.
- Man sollte immer mit der Berücksichtigung von Interaktionen zwischen den Toleranzgrößen beginnen. Nur so kann man feststellen, ob wirklich Wechselwirkungen zwischen den Toleranzgrößen existieren.
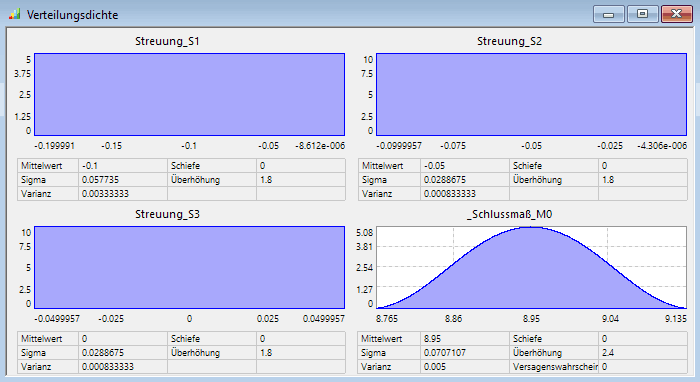
- Mittels Analyse > Probabilistik > Verteilungsdichte öffnen wir ein Grafikfenster und ziehen per Drag&Drop die Streuungen und das Schlussmaß (Restriktion!) aus dem OptiY-Explorer in dieses Fenster.
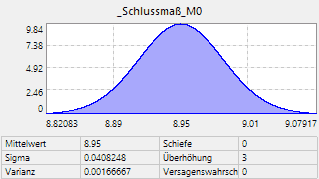
- Nach Projekt > Start erfolgt die Simulation der Stichprobe und die Verteilungsdichten der gewählten Größen werden dargestellt. Leider kann man anhand der dargestellten Grenzwerte von Schlussmaß_M0 nur näherungsweise die tatsächlichen Grenzen abschätzen. OptiY schneidet Werte der Dichtefunktion ab, die kleiner als 1/100 ihres Maximalwertes sind:
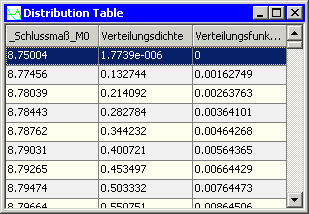
- Mittels Analyse > Probabilistik > Verteilungstabelle erhält man Stützstellen der Verteilungsfunktion aller Bewertungsgrößen (Restriktionen und Kriterien) für den Wertebereich von 0 bis 1 aufgelistet.
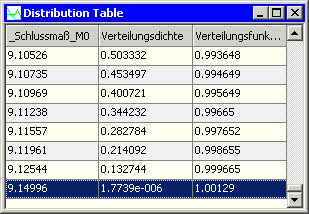
- In der ersten und letzten Zeile der Verteilungstabelle findet man nun die gesuchten Grenzen für das Schlussmaß:
- Bis auf geringe Rundungsfehler haben entspricht dies den Werten der klassischen Maximum-Minimum-Methode.
Das Ergebnis der Maximum-Minimum-Methode bedeutet:
Bei den vorgegebenen Fertigungsgenauigkeiten liegt mit einer Wahrscheinlichkeit von 100% das Schlussmaß innerhalb der Grenzen 8,95±0,2.
Wahrscheinlichkeitsbasierte Methode
Der Vorteil der probabilistischen Simulation ist die Anschaulichkeit der grafischen Ergebnisdarstellung:
- So gibt es bei vielen Betrachtern sicher ein gewisses Aha-Erlebnis, dass trotz gleichverteilter Einzelmaße das Schlussmaß im Prinzip einer Normalverteilung entspricht.
- Es zeigt sich z.B. eine Häufung des Schlussmaßes in der Nähe des Toleranzmittenmaßes.
- Nur ein geringer Prozentsatz einer Stichprobe liegt mit dem Schlussmaß in der Nähe der Grenzwerte.
An dieser Erkenntnis setzt die wahrscheinlichkeitsbasierte Methode der Toleranzrechnung an:
- Alle unabhängigen Maße streuen um ihr Toleranzmittenmaß mit einer Verteilungsfunktion, welche von unterschiedlichsten Einflussgrößen abhängt.
- Im Normalfall oder bei mangelhafter Kenntnis der Verteilungsfunktionen kann man von einer Normalverteilung ausgehen.
- Die Verteilungsfunktion des Schlussmaßes ist abhängig von der Struktur der Maßkette und den Verteilungsfunktionen der Einzelmaße.
Für lineare Ketten kann man die Toleranz T0 des Schlussmaßes auf der Grundlage des quadratischen Toleranzfortpflanzungsgesetzes (Spezialfall des Fehlerfortpflanzungsgesetzes) analytisch berechnen:
- Der Streuungskoeffizient ci der Einzelmaße ist abhängig von der Verteilungsfunktion (0,333 für Normalverteilung).
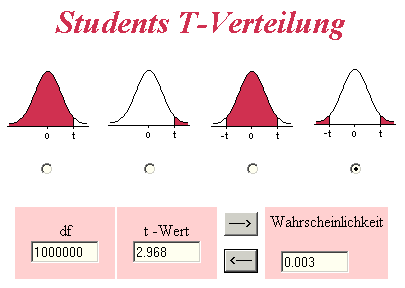
- Der Risikofaktor t für die Toleranz des Schlussmaßes ist abhängig davon, wieviel Prozent der Stichprobe im berechneten Toleranzbereich liegen sollen. Dabei wird die Student-t-Verteilung zugrunde gelegt:
- Bei vorgegebener Ausfallwahrscheinlichkeit (im Beispiel 0,3%, was T0=6•σ entspricht), kann man über einen Web-Rechner in der Uni Köln nach Wahl des Ausfallbereiches, der Angabe eines großen Wertes df=1000000 und der Wahrscheinlichkeit des Ausfalls von z.B. 0.003 den exakten Wert von t=2.968 erhalten:
- Die Toleranzbreite T0 berechnet man mit diesen Werten:
- [math]\displaystyle{ T_0=2{,}968 \cdot \sqrt{(0{,}333 \cdot 0{,}1 )^2+(0{,}333 \cdot 0{,}1)^2+(0{,}333 \cdot 0{,}2)^2}=0{,}2421 }[/math]
- Damit ergibt sich das Schlussmaß zu M0= 8,95±0,121 (normalverteilt).
Das bedeutet:
Bei gleichen Fertigungsgenauigkeiten wird eine reduzierte Schlussmaß-Toleranz erreicht! Es wird mit 99,7% Wahrscheinlichkeit im Beispiel ein Schlussmaß innerhalb der Grenzen 8,95 ± 0,12602 eingehalten.
Das werden wir nun in einem weiteren Experiment mit unserem Workflow-Modell anschaulich nachvollziehen:
- Dazu erstellen wir zuerst ein neues Experiment Wahrscheinlichkeit durch Duplizieren des Maximum-Minimum-Experiments (Kontextmenü der rechten Maustaste). Die Kopie des Experiments erhält durch anschließendes Umbenennen den gewünschten Namen.
- Wichtig: Das neue Experiment ist als "Startup-Experiment" auszuwählen. Erst damit wird es zum aktiven Experiment!
- Beim Kopieren werden der Workflow und alle Experiment-Einstellungen der Kopier-Vorlage übernommen. Die Darstellung der Ergebnisse muss man jedoch erneut mittels des Analyse-Menüs konfigurieren.
- Für alle Einzel-Toleranzen wählen wir anstatt der Gleichverteilung die Normalverteilung:
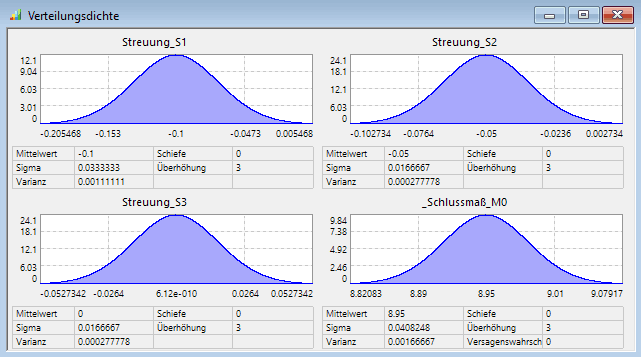
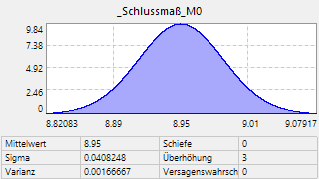
- Die anschließende Simulation ergibt eine Standard-Abweichung σ0=0,0408248 für das Schlussmaß:
- Damit ergibt sich eine Toleranz T0 = 6•σ = 0,245 und das Schlussmaß zu M0= 8,95±0,1225. Die mit dem Workflow-Modell ermittelte Toleranz des Schlussmaßes weicht im Beispiel ungefähr 1% (ca. 3 µm) vom Wert des analytischen Ansatzes ab. Diese zu vernachlässigende Abweichung resultiert wahrscheinlich aus den Näherungen des analytischen Ansatzes, da OptiY die probabilistische Simulation mit den exakten Verteilungen durchführt.
Toleranz-Optimierung
Bisher haben wir nur Toleranz-Analysen durchgeführt. D.h., wir erhielten Aussagen, wie sich gegebene Toleranzen auf ein Schlussmaß auswirken. An solche Analysen sollte sich folgerichtig eine Optimierung der Toleranzkette anschließen. Diese kann unter Einbeziehung unterschiedlichster Anforderungen erfolgen, z.B.:
- Bei vorgegebenem Schlussmaß sind die Einzelmaße so zu tolerieren, dass eine vorgegebene maximale Ausschussquote nicht überschritten wird.
- Zusätzlich können Vorgaben und Wichtungen für die Tolerierung der Einzelmaße vorgenommen werden. Damit lassen sich sowohl Fertigungsrestriktionen als auch Fertigungskosten berücksichtigen.
Dafür werden wir ein neues Experiment mit einem erweiterten Workflow-Modell konfigurieren:
- Wir duplizieren das Experiment Wahrscheinlichkeit und nennen das neue Experiment Toleranz-Maximierung (und wählen es als Startup-Experiment!):
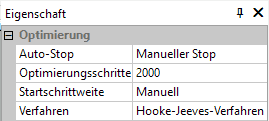
- Das Verfahren der Optimierung ist nun nicht mehr Simulation, sondern wir wählen das Hooke-Jeeves-Verfahren für die Suche einer optimalen Lösung. Das Hooke-Jeeves-Verfahren besitzt den Vorteil, dass man die Lösungssuche anhand der zielgerichteten Veränderungen der Optimierungsvariablen und der resultierenden Veränderungen der Bewertungsgrößen sehr gut verfolgen kann.
- Die Startschrittweite für die Abtastung der Zielfunktion stellen wir an den einzelnen Optimierungsvariablen manuell ein. Die Anzahl der Optimierungsschritte setzen wir mit z.B. 2000 sehr hoch an. Wir können die Optimierung aber jederzeit manuell stoppen:
- Im Beispiel erfolgte die ursprünglich Dimensionierung der Einzeltoleranzen nach der Maximum-Minimum-Methode bei Vorgabe der zulässigen Schlussmaß-Grenzen. Damit wurde eine 100%-ige Erfüllung für des Schlussmaß erreicht. Mit unserem ersten Experiment konnten wir das dann auch bestätigen.
- Da die Vorgabe der Schlussmaß-Grenzen unter der Sicht sowohl der Montage, als auch unter dem Aspekt einer sicheren Funktion erfolgte, sollen diese Grenzen im Weiteren als gegeben angenommen werden (M0=8,95±0,2).
- Zur Vorgabe dieser Soll-Toleranz des Schlussmaßes erweitern wir den Workflow um einen Nennwert Toleranz_T0_soll:
- Die Toleranzen Ti der unabhängigen Maße müssen wir als Variable für die Optimierung freigeben und mit sinnvollen Grenzen versehen. Als obere Grenze kann man den Wert von Toleranz_T0_soll verwenden, der untere Grenzwert wird durch die Fertigungsmöglichkeiten beschrieben (z.B. 50 µm):
- Die Startschrittweite für die Abtastung der Zielfunktion sollte ungefähr 1/1000 des aktuellen Toleranzwertes betragen.
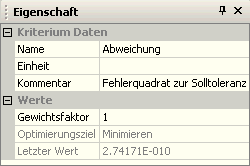
- Wir benötigen im Workflow-Modell noch ein Gütekriterium für die Abweichung der aktuellen Schlusstoleranz von der Vorgabetoleranz. Zusätzlich sollte die aktuelle Schlussmaß-Toleranz als separate Größe berechnet werden. Wir benutzen dafür wieder eine Restriktionsgröße:
- Die _Toleranz_T0 des Schlussmaßes berechnet man aus der Standardabweichung des Schlussmaßes:
- Die Abweichung wird als Fehlerquadrat berechnet. Die dafür benötigte aktuelle Toleranz des Schlussmaßes ermittelt man erneut aus der aktuellen Standardabweichung des Schlussmaßes, weil man auf die Werte der Restriktionsgröße _Toleranz_T0 in einem Formelausdruck nicht zugreifen kann:
In OptiY ist die Toleranzbreite T als der 6-fache Wert der Standardabweichung σ definiert. Damit erfasst man 99,7% aller möglichen Werte des streuenden Maßes. Um den Einstieg nicht unnötig kompliziert zu gestalten, werden wir deshalb bei der wahrscheinlichkeitsbasierten Toleranzoptimierung von einer zulässigen Ausschussquote von 0,3% ausgehen:
- Wir können die implemtierten Toleranzbereiche von OptiY benutzen.
- Die Optimierung verfolgt nach ihrem Start das Ziel, die Werte für alle Gütekriterien zu minimieren (Siehe rechtes Bild):
- Explizit haben wir nur die Abweichung von der Soll-Toleranz als Kriterium definiert.
- Infolge der definierten Restriktionen wird eine Straf-Funktion definiert, deren Wert Strafe=0 ist, wenn die Restriktionsgrößen für die Nennwert-Simulation eingehalten werden. Da wir die Grenzen sehr groß gewählt haben, spielen Restriktionsverletzungen in diesem Beispiel keine Rolle.
- Da wir eine infolge der Streuungen probabilistische Simulationen durchführen, wird die Versagenswahrscheinlichkeit als weiteres Gütekriterium betrachtet. In unserem Fall gilt immer Versagen=0, da infolge der praktisch "unbegrenzten" Restriktionsgrößen sich die gesamte Stichprobe innerhalb der Grenzen befindet.
- Berücksichtigt werden jedoch die Kosten für die Realisierung der Toleranzen. Die Kosten Ki für die Realisierung der Einzel-Toleranz Ti betragen Ki=(1E-6)/Ti. Die Summe der gewichteten Einzelkosten wird minimiert.
- Bei Verwendung des Hooke-Jeeves-Verfahrens der Optimierung erfolgt im Beispiel eine Minimierung der gewichteten Summe aus den Kosten und der Abweichung. Man muss also beobachten, ob bei der Optimierung die Abweichung zur Vorgabetoleranz hinreichend klein wird. Ansonsten muss man den Gewichtsfaktor für die Abweichung entsprechend vergrößern:
Für die erste Optimierung betrachten wir alle Einzeltoleranzen der unabhängigen Maße als gleichberechtigt. Wir belassen für alle Streuungen Kostenfaktor=1, was dem Standardwert für eine Streuung entspricht:
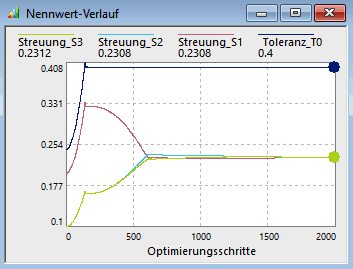
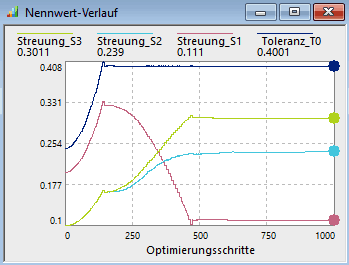
- Im Nennwert-Verlauf werden von den Streuungen die aktuellen Toleranz-Werte angezeigt.
- Ausgehend von den Anfangswerten der Einzeltoleranzen werden diese vergrößert, bis die Vorgabe-Toleranz von 0,4 mm für das Schlussmaß erreicht ist.
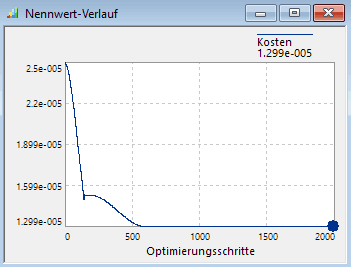
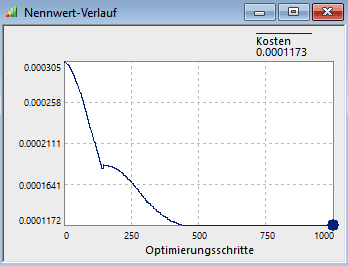
- Man kann beobachten, dass dabei natürlich auch die Kosten für die Toleranzen sinken:
- Nach Erreichen der Vorgabe-Toleranz für das Schlussmaß (Knick in Kosten-Verlauf) erfolgt auf Basis einer weiteren Kosten-Minimierung eine Verschiebung der Einzel-Toleranzen zueinander.
- Am Ende der Optimierung besitzen alle unabhängigen Maße praktisch die gleiche Toleranz, was einem Minimum der Toleranz-Kosten entspricht.
Im Normalfall sind je Fertigungsverfahren die einzelnen Toleranzwerte unterschiedlich Kostenaufwändig in ihrer Realisierung. Die relativen Kosten zwischen den einzelnen Toleranzen können über Kostenfaktoren berücksichtigt werden. Wir setzen im Beispiel:
- KostenfaktorT1=1
- KostenfaktorT2=10
- KostenfaktorT3=20
Nach einem erneuten Start der Optimierung sehen wir eine deutliche Verschiebung der Einzel-Toleranzen im Vergleich zur vorherigen Lösung:
- Je aufwändiger ein Toleranzwert zu realisieren ist, desto gröber wird das Maß toleriert.
- Die berechneten Kosten sind auf Grund der Kostenfaktoren>1 größer als zuvor. Es handelt sich hierbei jedoch nur um ein "Maß für die Gesamtkosten" und nicht um die tatsächlichen Fertigungskosten:
- Dadurch deutet sich ein Problem an, welches im Beispiel noch keine Relevanz besitzt:
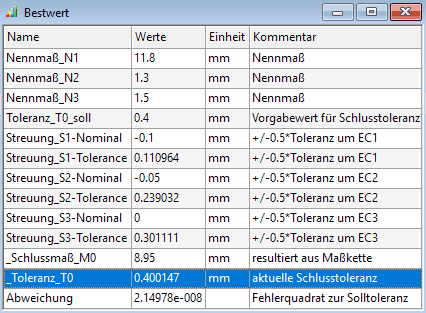
- Da die berechnete Abweichung nun im Verhältnis zu den Kosten ein etwas geringeres Gewicht in der zu minimierenden Summe beider Werte besitzt, wird die Vorgabe-Toleranz für das Schlussmaß nicht mehr ganz erreicht (im Beispiel T0=0,400147):
- Wenn das stört, muss man den Formel-Ausdruck für das Gütekriterium Abweichung um einen Faktor >1 ergänzen. Diesen Faktor kann man in Zehnerpotenzen vorsichtig erhöhen. Im Beispiel gelang mit dem Faktor=10 eine "exakte" Einhaltung der Vorgabe-Toleranz.
- Hinweise:
- Eine zu große Gewichtung der Abweichung führt zu einer schlechteren Konvergenz zur optimalen Lösung!
- Die Erhöhung des Gewichtsfaktors für das Gütekriterium "Abweichung" im OptiY-Explorer ist nicht möglich, da dessen Wert nur zwischen 0 und 1 geändert werden kann!
Eigenschaften des Toleranzmodells
Obwohl unser Workflow-Modell sehr schnell rechnet, kann es nie schaden, den Zeitaufwand für die probabilistische Simulation zu minimieren. Wir nutzten bisher für die statistische Versuchsplanung das Momentverfahren der Second Order Analyse unter Berücksichtigung von Interaktionen zwischen den Toleranzgrößen. Innerhalb der Momentverfahren ist dies die aufwändigste Methode, welche pro Simulation einer Stichprobe bei n Toleranzgrößen (2n²+1) Modellberechnungen benötigt. Bei einer größeren Zahl von Toleranzgrößen steigt die Berechnungszeit sehr schnell an!
Für die Untersuchung der Modelleigenschaften sollte man ein separates Experiment im OptiY-Versuchsstand konfigurieren:
- Wir Duplizieren dazu z.B. das Experiment Wahrscheinlichkeit und nennen das neue Experiment Modelleigenschaft.
- Die Konfiguration der probabilistischen Simulation können wir beibehalten.
1. Ordnung des Ersatzmodells
Für jede im Workflow definierte Bewertungsgröße (Restriktion, Gütekriterium) wird eine Ersatzfunktion auf Basis einer Taylorreihe gebildet. Für die Momenten-Methode sind Taylor-Reihen erster oder zweiter Ordnung verwendbar:
- First Order: nur lineare Abhängigkeiten zwischen den Toleranzen und der Bewertungsgröße können abgebildet werden.
- Second Order: Nichtlinaeritäten werden als quadratische Ersatzfunktion abgebildet.
Bei einer linearen Maßkette weiß man, dass ein linearer Zusammenhang zwischen den unabhängigen Toleranzgrößen und der Schlussmaß-Toleranz besteht. Falls dies nicht augenscheinlich ist, hilft nur eine vergleichende Simulation mit unterschiedlicher Ordnung. Wir werden hoffentlich sehen, dass ein Ansatz erster Ordnung ausreicht:
- Das erste Bild zeigt die Verteilungsdichte des Schlussmaßes berechnet mit First-Order-Ansatz.
- Da es zur Berechnung nach dem Second-Order-Ansatz im zweiten Bild keinerlei Unterschied gibt, kann man im Weiteren für die Versuchsplanung den linearen Ansatz verwenden.
- Damit reduziert sich die Anzahl der Modellberechnung bei n Toleranzgrößen von (2n²+1) auf (2n²-n+1), was bei einer größeren Anzahl von Toleranzgrößen jedoch nur eine geringe Rechenzeit-Ersparnis bringt.
2. Interaktionen zwischen Toleranzgrößen
Wenn die Reaktion einer Bewertungsgröße auf die Änderung einer Toleranzgröße vom aktuellen Istwert einer anderen Toleranzgröße abhängt, spricht man von Interaktion. Die Berücksichtigung der Interaktionen zwischen den Toleranzgrößen erfordert den größten Anteil an der Anzahl der erforderlichen Modellberechnungen:
- Um zu erkennen, ob merkliche Interaktionen zwischen den Toleranzgrößen existieren, muss man eine probabilistische Simulation unter Berücksichtigung der Interaktionen durchführen (im Beispiel bereits mit "First Order").
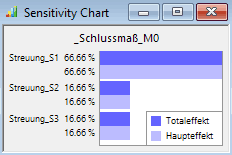
- Über Analyse > Sensitivität > Sensitivität-Chart erhält man ein leeres Grafikfenster, in welches man per Drag&Drop interessierende Bewertungsgrößen zieht (im Beispiel nur _Schlussmaß_M0).
- Entscheidend ist nun, ob es einen relevanten Unterschied zwischen Total- und Haupteffekt für die einzelnen Toleranzgrößen gibt. Der Totaleffekt berücksichtigt im Unterschied zum Haupteffekt auch den Einfluss der anderen Toleranzen:
- In unserem Beispiel ist erwartungsgemäß kein Unterschied zu erkennen, es existieren also keine Interaktionen.
- Im Weiteren können wir also lineare Maßketten grundsätzlich ohne Berücksichtigung von Interaktionen simulieren. Damit beträgt der Berechnungsaufwand nur noch (n+1). Die Berechnungszeit für die Simulation einer Stichprobe steigt also nur noch proportional zur Anzahl der Toleranzgrößen n.
Diese optimale Konfiguration der statistischen Versuchsplanung sollte man auch für das Optimierungsexperiment verwenden. Die damit erhaltenen Ergebnisse sind exakt die gleichen, wie mit dem aufwändigsten Momenten-Verfahren.