Grundlagen: Probabilistik - Analysen

Hinweis: Dieses Kapitel wird zur Zeit erarbeitet

Zielstellung

Mittels statistischer Versuchsplanung (DoE) kann auf der Grundlage deterministischer Modelle das Verhalten von Stichproben im Streu-Bereich der betrachteten Input-Größen simuliert werden. Dabei werden größere Mengen an Daten produziert.

Zielstellung für die probabilistischen Analyse ist die Aufbereitung dieser DoE-Daten in einer Form, welche die Wirkung der streuenden Input-Größen auf das Systemverhalten möglichst anschaulich und umfänglich darstellt. Für unterschiedliche Aspekte des Systemverhaltens werden dazu Diagramme mit unterschiedlichsten Darstellformen genutzt.

Welche Informationen man welchen Diagrammen entnehmen kann, wird bei der Beschreibung der einzelnen Diagramm-Typen erläutert.

Reale Stichprobe

Unabhängig vom gewählten DoE-Verfahren müssen entsprechend des zugehörigen Versuchsplans verschiedene Parameter-Kombinationen im Streu-Bereich der betrachteten Input-Größen mit dem Modell des realen Objektes berechnet werden. Im klassischem Sinne entspricht dies der Messung an Exemplaren einer "realen Stichprobe" bzw. an speziell konfigurierten realen Versuchsobjekten.

Die folgenden Analyse-Möglichkeiten beziehen sich auf die Daten, welche mittels eines speziellen Versuchsplans am "realen" (Modell-)Objekt berechnet bzw. gemessen wurden.

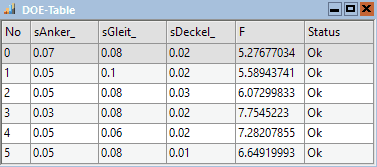
DoE-Tabelle

Jede Zeile dieser Tabelle entspricht einem Exemplar der realen Stichprobe (= eine Stützstelle im Streu-Bereich):

• Prinzipiell könnte man dort alle Datenwerte aufnehmen, welche bei der Berechnung / Messung der einzelnen Stützstellen anfallen.
• In praktischen Anwendungen muss man sich jedoch auf Grund der Datenmenge auf eine Teilmenge aussagekräftiger Daten beschränken.
• Man beschränkt sich meist auf die Werte der streuenden Input-Größen und der sich daraus ergebenden Output-Größen (z.B. Second Order Analyse ohne Interaktionen für die streuenden Luftspalte und die zugehörige Magnetkraft mit dem Modell eines Elektro-Magneten):
  
• Nur erfolgreiche Abtastungen erhalten den Status Ok. Dies hat insbesondere Bedeutung für die Moment-Methode, welche jede Abtastung für die Bildung der Taylorreihen-Ersatzmodelle benötigt.
• Stützstellen mit dem Status Failed sind für die weitere probabilistische Analyse nicht benutzbar. Dies hat nur geringe Bedeutung z.B. für Sample-Verfahren, solange noch hinreichend viele erfolgreiche Abtastungen existieren.

Anthill-Plot

Der "Ameisenhaufen" stand Pate für die Bezeichnung dieser Darstellform (Punktdiagramm), welche auch als Streudiagramm (engl. Scatterplot) bekannt ist. Man unterscheidet nach Anzahl der Koordinatenachsen 2D- und 3D-Anthill-Plots. In Abhängigkeit davon, welche Variablen man die Koordinaten-Achsen zuordnet, existieren drei grundsätzliche Zielstellungen:

1. Stützstellen im Streu-Bereich der Input-Größen

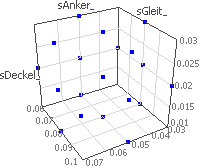
Belegt man alle Koordinatenachsen mit einer Teilmenge der streuenden Input-Größen, so erhält man einen Eindruck, wo innerhalb des gesamten Streu-Bereiches "Exemplare" der realen Stichprobe generiert wurden.

Im Beispiel wurde die drei toleranzbehafteten Luftspalte eines Elektro-Magneten den Koordinatenachsen eines 3D-Anthill-Plots zugewiesen. Dargestellt sind die Stützstellen des Second Ordner Moment-Verfahrens.

2. Zusammenhang zwischen Input-und Output-Größen

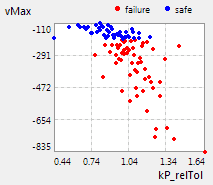
Belegt man die Abszissenachsen mit einer Teilmenge der streuenden Input-Größen und die Ordinatenachse mit einer Output-Größe, so erhält man einen Eindruck zu Korrelationen zwischen Input- und Output-Größen bzw. zu Clusterbildungen zwischen.

Im Beispiel wird die in der Spule eines Elektromagneten induzierte Abschaltspannung vMax in Abhängigkeit von der Steifigkeit kP eines mit Blindenschrift zu prägenden Papiers dargestellt.

3. Abhängigkeiten zwischen Output-Größen

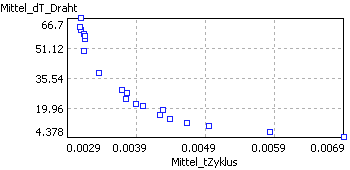
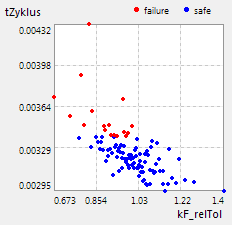
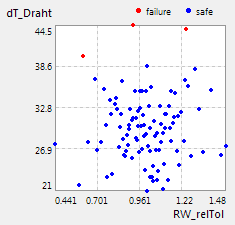
Die Gütekriterien eines Systems als Teilmenge der Output-Größen sind meist voneinander abhängig. Einen Eindruck zu diesen Abhängigkeiten erhält man, wenn man alle Achsen des Anthill-Plots nur mit Gütekriterien belegt.

Diese Kriterien sind miteinander oft nicht verträglich. Beim Versuch die Werte einiger Kriterien zu minimieren, können sich die Werte anderer Kriterien vergrößern. Im Beispiel des E-Magneten führt z.B. eine Verringerung der Zykluszeit tZyklus zu einer Temperaturerhöhung dT_Draht des Spulendrahtes.

Histogramme

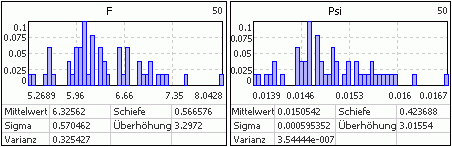
Histogramme stellen die Häufigkeitsverteilung der abgebildeten Größen innerhalb ihres Streubereiches dar. Diese Form der Darstellung ist nur sinnvoll für Sample-Methoden, um z.B. einen qualitativen Eindruck zu erhalten, in welchem Maße durch die Größe der realen Stichprobe die vorgegebene Verteilung der Input-Größen hinreichend nachgebildet wird:

Im Beispiel wird mit einer Stichprobengröße=50 die Normalverteilung der toleranzbehafteten Luftspalte eines E-Magneten zumindest andeutungsweise nachgebildet. Aus dieser diskreten Stichprobe ergibt sich dann eine Streuung der Output-Größen (im Beispiel die Magnetkraft F und der Koppelfluss Psi):

Korrelationen

Es wird für die reale Stichprobe die Korrelation zwischen allen Input-Streuungen und Output-Größen in Form von linearen Spearman Korrelationskoeffizienten dargestellt. Der Koeffizient K bewegt sich in einem Bereich von -1 bis +1:

• |K|=0 → keine Korrelation mit der Toleranzgröße
• |K|=1 → starke Korrelation mit der Toleranzgröße.
• Korrelationsmatrix: der Wert von K wird durch einen Farbwert gekennzeichnet.
• Korrelationstabelle: entspricht in ihrer Struktur der Korrelationsmatrix.
  
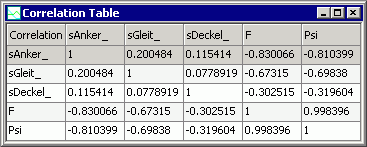
• Dargestellt werden die Werte konkreten Korrelationskoeffizienten.
• Damit erhält man für die echte Stichprobe nicht nur eine qualitative Orientierung zur Stärke der Korrelation, sondern auch die zugehörigen Korrelationswerte.

Interpretation:

• Entlang der Diagonalen ist K=1 (Jede Größe bildet mit sich selbst eine Gerade y=x).
• Eine starke Korrelation widerspiegelt sich in einem Anthill-Plot, indem die Lösungspunkte relativ dicht entlang einer gedachten Ausgleichsgeraden angeordnet sind:
  
• Kleine Korrelationskoeffizienten werden im Anthill-Plot durch eine ausgedehnte Punktwolke repräsentiert. D.h., die Werte der Ordinaten-Größe werden überwiegend von anderen Größen bestimmt:
  
• Zwischen den unterschiedlichen Input-Streuungen eines Modells darf keine Korrelation existieren (K=0), wenn die Bildung der Zufallszahlen gut funktioniert. Auf Grund relativ kleiner Stichproben ist z.B. K<0.2.

Wichtig: Korrelation bedeutet nicht "kausale Abhängigkeit"! In Modellen technischer Systeme verbirgt sich dahinter aber meist eine Ursache-Wirkungs-Beziehung.