Grundlagen: Optimierungsverfahren

Autor: Dr.-Ing. Alfred Kamusella

Globale Suchverfahren

Zielstellung

Die Zielstellung für globale Suchverfahren der Optimierung besteht darin, innerhalb eines vorgegebenen Suchraums den absoluten Extremwert (das globale Optimum) zu finden. Bei der Anwendung innerhalb eines Entwurfsprozesses entspricht dies der absolut besten Lösung. D.h., es existiert keine Lösung, welche der idealen Lösung näher kommt:

• Leider gibt es keine mathematischen oder numerischen Methoden, welche für Suchräume mit mehr als 2-3 Entwurfsparametern das Finden der absolut besten Lösung garantieren können. Findet man einen Extremwert auf Gütefunktion, so weiß man praktisch nie, ob es nicht doch noch eine bessere Lösung gibt.
• Deshalb setzt man globale Suchverfahren innerhalb von Entwurfsprozessen meist "nur" zu Analysezwecken ein. Man verschafft sich damit einen "Überblick" über die Zielfunktion im einen zuvor definierten Suchraum:
  • Innerhalb des Suchraums wird die Oberfläche der Zielfunktion in Form einzelner Abtastpunkte berechnet.
  • Man sollte versuchen, daraus die Eigenschaften der Zielfunktion zu erkennen:
    1. Vorhandensein lokaler Optima, Unstetigkeitsstellen,
    2. mögliche Position des globalen Optimums,
    3. sinnvolle Veränderung der Suchraums (Grenzen der Entwurfsparameter verschieben, erweitern oder einengen).
    4. sinnvolle Positionen von Startpunkten für lokale Suchverfahren.
• Ziel dieser Analyse ist das Ermitteln geeigneter Startpunkte für lokale Suchverfahren in einem sinnvoll definierten Suchraum.

Bei der globalen Analyse der Zielfunktion hat man mit diversen Problemen zu kämpfen:

• Der menschliche Blick auf mehrdimensionale Räume ist sehr eingeschränkt. So versagt bei mehr als 2 Entwurfsparametern recht schnell unsere Vorstellung.
• Man kann immer nur endlich viele ausgewählte Punkte des Suchraums berechnen und muss die Zielfunktion dann hinein interpolieren. Sind die Abstände zwischen den Punkten zu groß, gehen die Details dazwischen natürlich verloren.

Systematische Suche (Rastersuche)

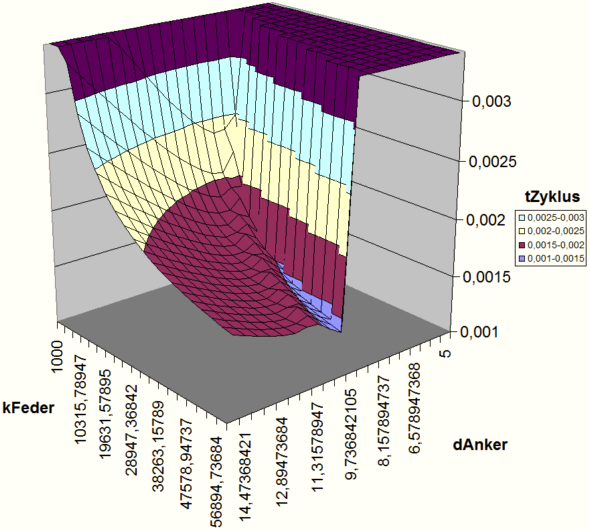
Die N Achsen der Entwurfsparameter werden innerhalb des Suchraums in gleichmäßige Abstände geteilt. Die Schnittpunkte der Rasterlinien definieren die Abtastpunkte auf der Oberfläche der Zielfunktion.

In der statistischen Versuchsplanung (design of experiments = DoE) ist dieses Verfahren auch als vollständiger Versuchsplan (full factorial design) bekannt:

• Im obigen Beispiel wurde für einen Elektromagneten die Zykluszeit in Abhängigkeit vom Ankerdurchmesser und der Rückholfeder untersucht.
• Das Verfahren der Rastersuche wird meist als Analyse-Werkzeug für die Eigenschaften einer Zielfunktion benutzt, um die Grundlage für den Einsatz lokaler Suchverfahren zu schaffen.
• Verfügt man über ein hinreichend schnell rechnendes Modell in einem kleinen Suchraum, kann man mit der Rastersuche natürlich auch iterativ recht schnell das mögliche Gebiet des globalen Optimums eingrenzen und dort sogar die exakte Position der bestmöglichen Lösung ermitteln:
  1. Voraussetzung ist eine Zielfunktion,welche in großen Bereichen monoton ist und Optima in ausgeprägten breiten Tälern aufweist.
  2. Unter dieser Voraussetzung gilt dann unabhängig von der Anzahl der Entwurfsparameter, dass man wahrscheinlich ein Optimum umschlossen hat, wenn der beste Abtastwert kein Randpunkt ist.
• Im Beispiel müsste man den Suchraum zu höheren Federkonstanten hin verschieben, um das globale Optimum zu umfassen.

Im obigen Diagramm wird nur die Gütefunktion "Zykluszeit" dargestellt, welche möglichst klein werden soll:

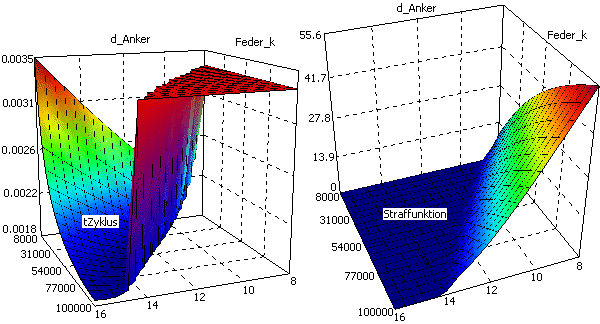
• Bei der Suche nach dem globalen Optimum muss man berücksichtigen, dass sich im abgetasteten Suchraum nur zulässige Lösungen befinden, wo keine Restriktionen für den Magnetantrieb verletzt werden (Wert der anhand der Restriktionen gebildeten Straf-Funktion = 0).
• Damit existiert zusätzlich zu den Werten der Gütefunktion für jeden Abtastpunkt mit dem Wert der Straf-Funtion eine Information, ob die für das Modell definierten Restriktionen eingehalten werden (ja/nein bzw. Grad der Verletzungsgrad).
• Der betrachtete Magnetantrieb soll mindestens eine Zykluszeit von 3,4 ms erreichen und seinen Bewegungsvorgang komplett ausführen:
  

Monte-Carlo-Simulation

Oft kann infolge langsamer Modelle oder einer Vielzahl von Entwurfsparametern mittels Rastersuche keine sinnvolle Analyse der Zielfunktion erfolgen. Die erforderliche Berechnungszeit für die notwendige Anzahl Stützstellen wäre einfach zu groß:

• Dann helfen zufällige Stützstellen (Monte-Carlo-Simulation) zumindest bei der Suche nach geeigneten Startpunkten für die lokale Suche:

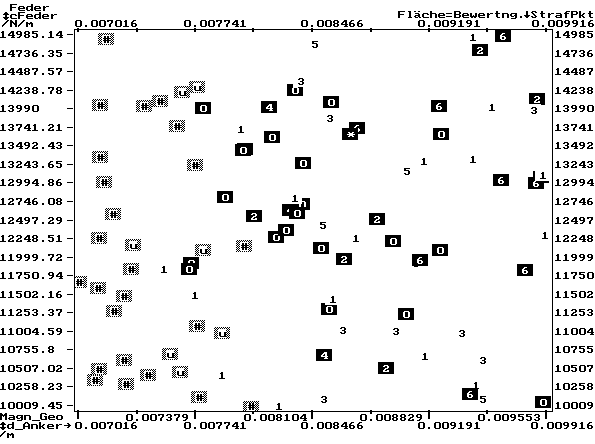
• Das Beispiel zeigt für den Magnetantrieb die Werte der Straffunktion in Abhängigkeit von Federkonstante und Ankerdurchmesser:
  • Der Stern * kennzeichnet die beste "erwürfelte" Lösung (Startpunkt für lokale Suche).
  • Die Ziffern repräsentieren den Wertebereich der Straffunktion.
  • Die anderen Symbole markieren Restriktionsverletzungen (z.B. u=überhöhte Spulenspannung / #=Mehrfach-Verletzungen))

Lokale Suchverfahren

Die Mehrzahl der verfügbaren Optimierungsverfahren sind Verfahren zur lokalen Suche:

• Lokale Suchverfahren sollen ausgehend von einem Startpunkt (Anfangslösung) möglichst das globale Optimum finden. In der Praxis wird jedoch nur ein lokales Minimum gefunden, welches vom Startpunkt aus durch schrittweise verbesserung der Lösung erreicht werden kann.
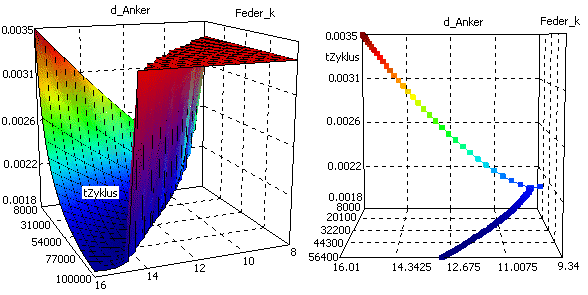
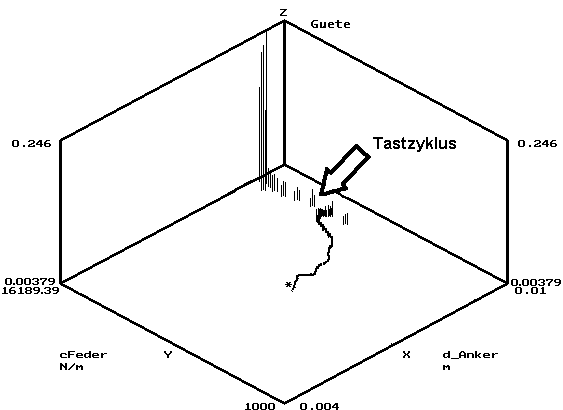
• Das folgende Bild zeigt den möglichen Pfad eines lokalen Suchverfahrens auf der Zielfunktion "Zykluszeit" des Magnetantriebes:

• Es erfolgt im Beispiel eine stetige Verbesserung der Zykluszeit entlang des "steilsten Abstiegs", bis die Lösung nicht mehr alle Forderungen erfüllt.
• Dann tastet sich das lokale Suchverfahren entlang der Restriktionsgrenze auf der Zielfunktion, bis keine bessere Lösung entlang dieser Grenze gefunden werden kann.

Zur Suche optimaler Lösungen für ein Entwurfsproblem eignen sich nur Methoden, welche keine analytische Ableitung der Zielfunktion benötigen:

• Die Zielfunktion in Entwurfsproblemen ist im Normalfall nicht als geschlossene Funktion gegeben. Sie ergibt sich nur punktuell durch Simulation einer konkreten Lösung im Suchraum der Entwurfsparameter.
• Eventuell vom Suchverfahren benötigte 1.Ableitungen können an einem Punkt im Suchraum näherungsweise durch Abtastung als Differenzenquotient gewonnen werden.
• Besonders effektiv sind Verfahren, welche wie im Beispiel ausgehend vom Startpunkt sich in Richtung des steilsten Abstiegs bewegen.
• Lokale Suchverfahren enden zwangsläufig, wenn sie auf dem Weg "nach Unten" eine Mulde erreicht haben. Ursache ist das "blinde" Abtasten einzelner Punkte der Oberfläche in der näheren Umgebung mit dem Ziel, beim nächsten Schritt etwas tiefer zu kommen. Deshalb sollte der Startpunkt im Bereich eines vermuteten globalen Optimums liegen.
• Klassische lokale Suchverfahren bewegen sich nur abwärts. Modernere Verfahren erlauben mit gewissen Wahrscheinlichkeiten auch eine Verschlechterung der Lösung, um aus kleineren Mulden wieder herauszufinden.

Abtastung der Zielfunktion mit Schrittweitenregelung (Beispiel "Hooke-Jeeves-Verfahren"):

• Die Steigung der Zielfunktion am Punkt der aktuell erreichten Lösung wird über kleine Tastschritte ermittelt. Die genutzte Tastschrittweite muss dabei der Oberfläche der Zielfunktion angepasst sein.
• In Richtung des ermittelten steilsten Abstiegs wird anschließend ein größerer Schritt ausgeführt:

• Die Tastschritte werden gleichzeitig zur Verbesserung der Lösung genutzt. Beim Tastzyklus wird von einem Startvektor aus nacheinander in jede Koordinatenrichtung ein diskreter Suchzyklus durchgeführt. Führt dabei der Tastschritt in einer Richtung nicht zum Erfolg (Verbesserung des Gütewertes), so wird zusätzlich die entgegen gesetzte Richtung abgetastet.
• Nach einem Tastphase erfolgt die Extrapolation. In Richtung des ermittelten steilsten Abstieges wird ein größerer Schritt ausgeführt. Ein erneuter Extrapolationsschritt ist immer doppelt so groß wie der vorherige, solange dabei eine Verbesserung des Zielfunktionswertes erreicht wird. Schießt das Verfahren über den tiefsten Punkt hinaus oder in einen verbotenen Bereich, erfolgt eine schrittweise Verringerung der Extrapolationsschrittweite.
• Das Hooke-Jeeves-Verfahren regelt die anfängliche Tastschrittweite herunter, wenn längere Zeit keine Verbesserung des Zielfunktionswertes mehr erreicht werden konnte. Meist gelangt dann diese Schrittweite in Größenordnungen der stochastischen Rauigkeiten der Zielfunktion und das Optimierungsverfahren bleibt hängen, weil die partiellen Ableitungen total verfälscht werden (die reale Steigung wird nicht mehr erkannt).

Optimierung nach biologischem Vorbild

Einfuehrung

Die natürliche Evolution der Lebewesen hat erstaunliche Lösungen für das Funktionieren von Organismen in unterschiedlichsten ökologischen Nischen hervorgebracht. Die einzelnen Arten von Lebewesen stellen offensichtlich optimierte Lösungen für das Überleben in ihrer jeweiligen Umwelt dar.

Schon sehr früh haben Menschen begonnen, "Lösungen" der Natur auf die Technik zu übertragen. Das älteste dokumentierte Beispiel der systematischen Übertragung solcher Natur-Phänomene auf technische Objekte ist Leonardo da Vincis Idee, den Vogelflug auf Flugapparate zu übertragen. Seit ca. 1/2 Jahrhundert fasst man solche Bestrebungen unter dem Begriff Bionik zusammen.

Die sogenannten evolutionären Algorithmen sind eine Klasse von Optimierungsverfahren, deren Funktionsweise von der Evolution der Lebewesen inspiriert wurde. Ausgangspunkt für die Entwicklung von evolutionären Algorithmen ist eine Abstraktion der realen natürlichen Evolution auf das Grundprinzip ihrer Wirkungsweise.

Grundprinzip:

• Evolutionäre Algorithmen erzeugen aus einer Elterngeneration (von Parametersätzen) durch die genetischen Prozeduren (Mutation, Rekombination) eine Kindergeneration. Eine Teilmenge der Kinder wird nach Fitness-Selektion (anhand des Verhaltens) zur neuen Elterngeneration.
• Die Parameter der genetischen Prozeduren sind selbst Bestandteil der Optimierung (Mutationsraten, Art der Rekombination).
• Voraussetzung der Anwendung evolutionärer Verfahren auf ein System (z.B. Zielfunktion) ist, dass dieses eine hinreichende Kausalität zwischen Ursachen (Parameteränderungen) und Wirkungen (Verhaltensänderungen) vermittelt.

===>>> Dieses Kapitel wird zur Zeit erarbeitet !!! <<<===

Vorläufige weitere Gliederung:

Optimierung nach biologischem Vorbild

• :
• Genetische Algorithmen und Evolutionsstrategie
• Grundlagen zur Evolutionsstrategie
  • Genotyp und Phänotyp
  • Das Evolutionsfenster
  • Evolution der Evolutionsstrategie
  • Anwendungsbereiche und Grenzen
• Konfiguration von Evolutionsstrategien
  • Notation (Basisalgorithmus)
  • Notation (Rekombination)
  • Optimale Eltern-Anzahl
  • Optimale Kinder-Anzahl
  • Überleben der Eltern
  • Rekombinationstypen
  • Mutationsschrittweite
• Co-Evolutionäre Strategien
  • Mehrkriterienoptimierung
  • Co-Existenz in Ökosystemen
  • Co-Evolutionäre Algorithmen