Software: FEMM - Stromfluss - Flaechenwiderstand: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
kleiner Formatierungsfehler |
||
| (12 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<div align="center"> [[Software:_FEMM_-_Stromfluss|←]] [[Software:_FEMM_-_Stromfluss_-_L-Schnitt|→]] </div> | [[Software:_FEM_-_Tutorial_-_Elektrofluss|↑]] <div align="center"> [[Software:_FEMM_-_Stromfluss|←]] [[Software:_FEMM_-_Stromfluss_-_L-Schnitt|→]] </div> | ||
[[ | <div align="center"> [[Bild:Software_FEMM_-_Stromfluss_-_Widerstand_ungetrimmt.gif]] </div> | ||
</div> | <div align="center"> '''Dimensionierung des ungetrimmten Widerstands'''</div> | ||
Der Widerstand der Pasten wird als Flächenwiderstand '''R<sub>F</sub>''' in '''Ω'''/□ angegeben: | Der Widerstand der Pasten wird als Flächenwiderstand '''R<sub>F</sub>''' in '''Ω'''/□ angegeben: | ||
| Zeile 18: | Zeile 17: | ||
* Um ganz sicher zu gehen, wird die Streuung von σ<sub>F</sub> auf R<sub>N</sub> bezogen, so dass der Streubereich etwas größer angesetzt wird, als er um den kleineren Widerstandswert R<sub>u</sub> dann auftritt. Die zulässige Streuung von R<sub>N</sub> wird so berücksichtigt, dass man möglichst wenig Trimmen muss, um einen zulässigen Widerstandswert zu erreichen. Damit ergibt sich für den zu druckenden (unabgeglichenen) Widerstandswert: | * Um ganz sicher zu gehen, wird die Streuung von σ<sub>F</sub> auf R<sub>N</sub> bezogen, so dass der Streubereich etwas größer angesetzt wird, als er um den kleineren Widerstandswert R<sub>u</sub> dann auftritt. Die zulässige Streuung von R<sub>N</sub> wird so berücksichtigt, dass man möglichst wenig Trimmen muss, um einen zulässigen Widerstandswert zu erreichen. Damit ergibt sich für den zu druckenden (unabgeglichenen) Widerstandswert: | ||
<div align="center"> '''R<sub>u</sub> = R<sub>N</sub> · (1 - σ<sub>F</sub>/100 ) · (1 + σ<sub>zul</sub>/100)''' </div> | <div align="center"> '''R<sub>u</sub> = R<sub>N</sub> · (1 - σ<sub>F</sub>/100 ) · (1 + σ<sub>zul</sub>/100)''' </div> | ||
* Im Gebiet des Widerstandes oberhalb der Trimmkerbe mit der verbleibenden Restbreite | * Im Gebiet des Widerstandes oberhalb der Trimmkerbe mit der verbleibenden Restbreite '''B<sub>getr</sub>''' des Widerstands tritt die maximale Verlustleistung auf (Worst Case Resistor '''WCR'''). Meist wird die halbe Breite des Widerstands als max. Tiefe der Trimmkerbe angesetzt. | ||
* Die Verlustleistungsdichte des Worst-Case-Resistors '''P<sub>WCR</sub>''' kann aus der max. Verlustleistungsdichte der Paste '''P<sub>max</sub>''', der Widerstandsbreite '''B<sub>u</sub>''' und der Rest-Stegbreite '''B<sub>getrWCR</sub>''' berechnet werden: | * Die Verlustleistungsdichte des Worst-Case-Resistors '''P<sub>WCR</sub>''' kann aus der max. Verlustleistungsdichte der Paste '''P<sub>max</sub>''', der Widerstandsbreite '''B<sub>u</sub>''' und der Rest-Stegbreite '''B<sub>getrWCR</sub>''' berechnet werden: | ||
<div align="center"> '''P<sub>WCR</sub> = P<sub>max</sub> · B<sub>getrWCR</sub> / B<sub>u</sub>'''</div> | <div align="center"> '''P<sub>WCR</sub> = P<sub>max</sub> · B<sub>getrWCR</sub> / B<sub>u</sub>'''</div> | ||
| Zeile 25: | Zeile 24: | ||
* Aus dem Wert des ungetrimmten Widerstands '''R<sub>u</sub>''' und einem zunächst vorgegebenem '''L:B'''-Verhältnis ergibt sich der Flächenwiderstand '''R<sub>F</sub>'''. Wird eine gestreckte Rechteck-Form gewählt ('''L>B'''), so wird zuerst die Breite des ungetrimmten Widerstands berechnet (hier ohne Herleitung): | * Aus dem Wert des ungetrimmten Widerstands '''R<sub>u</sub>''' und einem zunächst vorgegebenem '''L:B'''-Verhältnis ergibt sich der Flächenwiderstand '''R<sub>F</sub>'''. Wird eine gestreckte Rechteck-Form gewählt ('''L>B'''), so wird zuerst die Breite des ungetrimmten Widerstands berechnet (hier ohne Herleitung): | ||
<div align="center"> <math>B_u=\sqrt{\frac{P_v \cdot R_F}{P_{WCR} \cdot R_u}}</math> </div> | <div align="center"> <math>B_u=\sqrt{\frac{P_v \cdot R_F}{P_{WCR} \cdot R_u}}</math> </div> | ||
* Die Länge ergibt sich aus dem gewählten '''B<sub>u</sub>''' zu: | |||
<div align="center"> <math>B_u=\frac{R_F \cdot L}{R_u}</math> </div> | |||
Dies soll nun am Beispiel der Übung mit folgenden Werten nachvollzogen werden: | |||
* '''R<sub>N</sub> = 240 Ω''' (Nennwert nach Trimmen) | |||
* '''σ<sub>zul</sub> = ±2%''' (zulässige Toleranz von RN) | |||
* '''σ<sub>F</sub> = ±30%''' (Fertigungsstreuung ungetrimmt) | |||
* '''P<sub>V</sub> = 0,2 W''' (Verlustleistung im Betrieb) | |||
* '''P<sub>max</sub>= 6,2 W/cm²''' (max. Leistungsdichte der Paste) | |||
* '''R<sub>F</sub>= dekadisch gestuft''' (Flächenwiderstand Paste) | |||
* '''B<sub>getrWCR</sub> = 0,5 · B<sub>u</sub>''' (Trimmkerbe maximal) | |||
Damit errechnet man die Schnittgeometrie: | |||
# ''Ungetrimmter Widerstandswert'' | |||
#:'''R<sub>u</sub>''' = 240 Ω · 0,7 · 1,02 = '''171,36 Ω''' | |||
# ''Max. zul. Leistungsdichte im Worst-Case-Resistor'' | |||
#:'''P<sub>WCR</sub>''' = 0,5 · 6,2 W/cm² = '''3,1 W/cm²''' | |||
# ''Vorauswahl einer Paste (durch Wahl L>B)'' | |||
#:'''R<sub>u</sub>= 171 Ω''' mit '''L/B=1,71''' ergibt '''R<sub>F</sub>=100 Ω/'''□ | |||
# ''Breite ungetrimmter Widerstand'' | |||
#:<math>\mathbf{B_{u}}=\sqrt{\frac{0,2W\cdot100\,\Omega/\Box}{3,1W/cm²\cdot171\,\Omega}}\approx\mathbf{2,0\, mm} </math> | |||
#:(im optimalen Bereich '''0,5 mm < Bu < 5 mm''', deshalb kein Versuch mit L<B erforderlich!) | |||
# ''Länge ungetrimmter Widerstand'' | |||
#:'''L''' = 171 Ω · 2,0 mm / 100 Ω/□ ='''3,42 mm''' | |||
<div align="center"> ''Siehe Hanke u.a.: „Baugruppentechnologie der Elektronik - Band Hybridträger“, Verlag Technik 1994'' </div> | |||
<div align="center"> '' ISBN 3341010998, ISBN 9783341010990 '' </div> | |||
<div align="center"> [[Software:_FEMM_-_Stromfluss|←]] [[Software:_FEMM_-_Stromfluss_-_L-Schnitt|→]] </div> | <div align="center"> [[Software:_FEMM_-_Stromfluss|←]] [[Software:_FEMM_-_Stromfluss_-_L-Schnitt|→]] </div> | ||
Aktuelle Version vom 3. März 2022, 07:35 Uhr
Dimensionierung des ungetrimmten Widerstands
Der Widerstand der Pasten wird als Flächenwiderstand RF in Ω/□ angegeben:
- Dies ist auf den ersten Blick etwas ungewöhnlich, aber letztendlich sehr praktisch. Es bedeutet, dass unabhängig von der Größe eine quadratische Fläche immer den angegebenen Widerstand zwischen zwei gegenüberliegenden Seitenflächen besitzt.
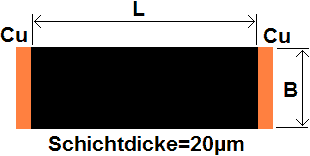
- D.h., bei einem Flächenwiderstand von 100 Ω/□ besitzen die folgenden Quadrate (unabhängig von ihrer Größe!) zwischen den Kontakten immer einen Widerstand Ru=100 Ω:
- Die unterschiedlich großen Widerstände besitzen jedoch eine unterschiedliche maximal mögliche Verlustleistung.
- Widerstandspasten werden für eine definierte Schichtdicke mit meist dekadisch gestaffelten RF=-Werten angeboten:20 Ω/□; 100 Ω/□; 1000 Ω/□; 10000 Ω/□; 100000 Ω/□.
- Weicht die Widerstandsform vom Quadrat ab, so berechnet sich der ungetrimmte Widerstand Ru eines Rechtecks zu
Ru = RF · L/B
Durch Lasertrimmen soll aus dem ungetrimmten Widerstand Ru (Fertigungstoleranz σF) ein Widerstandswert RN (mit der zulässigen Toleranz σzul) erzeugt werden:
- Durch das Trimmen wird der Widerstandswert vergrößert, d.h. der zu realisierende Widerstand RN muss größer sein als Ru.
- Die folgende Ungleichung sichert, dass alle gefertigten Widerstände in den Sollbereich hinein getrimmt werden können:
Ru + σF ≤ RN - σzul
- Um ganz sicher zu gehen, wird die Streuung von σF auf RN bezogen, so dass der Streubereich etwas größer angesetzt wird, als er um den kleineren Widerstandswert Ru dann auftritt. Die zulässige Streuung von RN wird so berücksichtigt, dass man möglichst wenig Trimmen muss, um einen zulässigen Widerstandswert zu erreichen. Damit ergibt sich für den zu druckenden (unabgeglichenen) Widerstandswert:
Ru = RN · (1 - σF/100 ) · (1 + σzul/100)
- Im Gebiet des Widerstandes oberhalb der Trimmkerbe mit der verbleibenden Restbreite Bgetr des Widerstands tritt die maximale Verlustleistung auf (Worst Case Resistor WCR). Meist wird die halbe Breite des Widerstands als max. Tiefe der Trimmkerbe angesetzt.
- Die Verlustleistungsdichte des Worst-Case-Resistors PWCR kann aus der max. Verlustleistungsdichte der Paste Pmax, der Widerstandsbreite Bu und der Rest-Stegbreite BgetrWCR berechnet werden:
PWCR = Pmax · BgetrWCR / Bu
- Die minimal erforderliche Fläche AW für den Widerstand ergibt sich dann aus der umzusetzenden Verlustleistung PV und der Verlustleistungsdichte für den Worst-Case-Resistor:
AW = PV / PWCR
- Aus dem Wert des ungetrimmten Widerstands Ru und einem zunächst vorgegebenem L:B-Verhältnis ergibt sich der Flächenwiderstand RF. Wird eine gestreckte Rechteck-Form gewählt (L>B), so wird zuerst die Breite des ungetrimmten Widerstands berechnet (hier ohne Herleitung):
[math]\displaystyle{ B_u=\sqrt{\frac{P_v \cdot R_F}{P_{WCR} \cdot R_u}} }[/math]
- Die Länge ergibt sich aus dem gewählten Bu zu:
[math]\displaystyle{ B_u=\frac{R_F \cdot L}{R_u} }[/math]
Dies soll nun am Beispiel der Übung mit folgenden Werten nachvollzogen werden:
- RN = 240 Ω (Nennwert nach Trimmen)
- σzul = ±2% (zulässige Toleranz von RN)
- σF = ±30% (Fertigungsstreuung ungetrimmt)
- PV = 0,2 W (Verlustleistung im Betrieb)
- Pmax= 6,2 W/cm² (max. Leistungsdichte der Paste)
- RF= dekadisch gestuft (Flächenwiderstand Paste)
- BgetrWCR = 0,5 · Bu (Trimmkerbe maximal)
Damit errechnet man die Schnittgeometrie:
- Ungetrimmter Widerstandswert
- Ru = 240 Ω · 0,7 · 1,02 = 171,36 Ω
- Max. zul. Leistungsdichte im Worst-Case-Resistor
- PWCR = 0,5 · 6,2 W/cm² = 3,1 W/cm²
- Vorauswahl einer Paste (durch Wahl L>B)
- Ru= 171 Ω mit L/B=1,71 ergibt RF=100 Ω/□
- Breite ungetrimmter Widerstand
- [math]\displaystyle{ \mathbf{B_{u}}=\sqrt{\frac{0,2W\cdot100\,\Omega/\Box}{3,1W/cm²\cdot171\,\Omega}}\approx\mathbf{2,0\, mm} }[/math]
- (im optimalen Bereich 0,5 mm < Bu < 5 mm, deshalb kein Versuch mit L<B erforderlich!)
- Länge ungetrimmter Widerstand
- L = 171 Ω · 2,0 mm / 100 Ω/□ =3,42 mm
Siehe Hanke u.a.: „Baugruppentechnologie der Elektronik - Band Hybridträger“, Verlag Technik 1994
ISBN 3341010998, ISBN 9783341010990