Software: FEM - Tutorial - Einleitung: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
|||
| (9 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Software:_FEM_-_Tutorial|↑]] <div align="center"> [[Software:_FEM_-_Tutorial|←]] [[Software:_FEM_-_Tutorial_-_Zielstellung|→]] </div> | [[Software:_FEM_-_Tutorial|↑]] <div align="center"> [[Software:_FEM_-_Tutorial|←]] [[Software:_FEM_-_Tutorial_-_Zielstellung|→]] </div> | ||
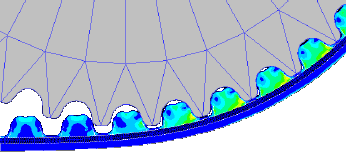
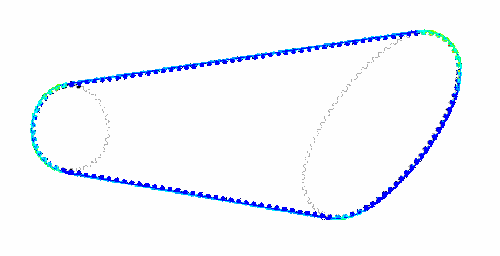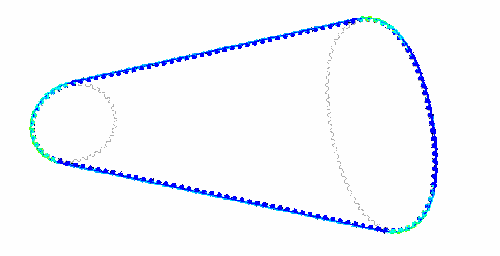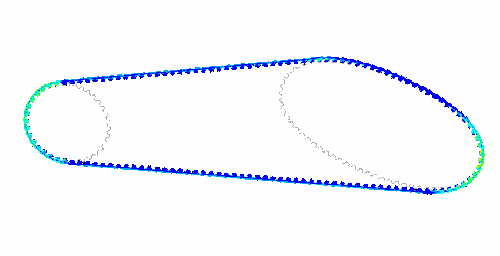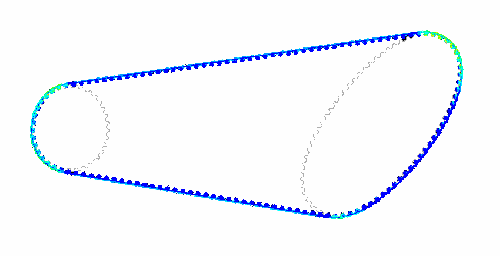
<div align="center"> Bild: Original und Finite-Element-Modell (Details von Zahnriemen und -scheibe):</div> | |||
<div align="center"> [[Bild:Software_FEM_-_Tutorial_-_Einleitung_-_zahnriemengetriebe_objekt.gif| ]] [[Bild:Software_FEM_-_Tutorial_-_Einleitung_-_zahnriemengetriebe_detail.gif| ]]</div> | <div align="center"> [[Bild:Software_FEM_-_Tutorial_-_Einleitung_-_zahnriemengetriebe_objekt.gif| ]] [[Bild:Software_FEM_-_Tutorial_-_Einleitung_-_zahnriemengetriebe_detail.gif| ]]</div> | ||
Die Finite-Elemente-Methode ([ | |||
Die Finite-Elemente-Methode ([https://de.wikipedia.org/wiki/Finite-Elemente-Methode '''FEM''']) ist ein numerisches Verfahren zur näherungsweisen Lösung von partiellen Differentialgleichungen mit Randbedingungen. | |||
Die Lösungen dieser partiellen Differentialgleichungen beschreiben die räumliche und auch zeitliche Verteilung der zugehörigen physikalischen Größen in einem betrachteten Raumgebiet. Man erhält im Ergebnis für das Innere eines räumlichen Objektes z.B.: | Die Lösungen dieser partiellen Differentialgleichungen beschreiben die räumliche und auch zeitliche Verteilung der zugehörigen physikalischen Größen in einem betrachteten Raumgebiet. Man erhält im Ergebnis für das Innere eines räumlichen Objektes z.B.: | ||
| Zeile 13: | Zeile 14: | ||
* Verläufe elektrischer und magnetischer Felder | * Verläufe elektrischer und magnetischer Felder | ||
Damit kann man sowohl die Belastung des betrachteten Objekts als auch seine Wirkung auf die Umgebung berechnen. Deshalb ist die praktische Anwendung dieser Methode für Konstrukteure sehr interessant, wenn da nicht die Hürden der Mathematik wären! Leider führt fast jede Einführung zur FEM unweigerlich über die grundlegenden Vektordifferentialgleichungen und über die Verfahren ihrer numerischen Lösung. Das kann den | Damit kann man sowohl die Belastung des betrachteten Objekts als auch seine Wirkung auf die Umgebung berechnen. Deshalb ist die praktische Anwendung dieser Methode für Konstrukteure sehr interessant, wenn da nicht die Hürden der Mathematik wären! Leider führt fast jede Einführung zur FEM unweigerlich über die grundlegenden Vektordifferentialgleichungen und über die Verfahren ihrer numerischen Lösung. Das kann den Einsteiger schon etwas abschrecken! | ||
=== FEM-Simulationen in CAD-Umgebungen === | === FEM-Simulationen in CAD-Umgebungen === | ||
| Zeile 20: | Zeile 22: | ||
Die Möglichkeiten solcher FEM-Simulationen innerhalb von CAD-Systemen sind im Vergleich zu FEM-Systemen zur Zeit noch begrenzt: | Die Möglichkeiten solcher FEM-Simulationen innerhalb von CAD-Systemen sind im Vergleich zu FEM-Systemen zur Zeit noch begrenzt: | ||
* | * Häufig nur für lineare Probleme, d.h. mit konstanten Materialkennwerten. | ||
* Strukturmechanik, teilweise in Wechselwirkung mit Temperaturfeldern. | * Strukturmechanik, teilweise in Wechselwirkung mit Temperaturfeldern. | ||
* Häufig schon Strömungsmechanik, zugeschnitten auf Spritzguss-Probleme. | * Häufig schon Strömungsmechanik, zugeschnitten auf Spritzguss-Probleme. | ||
| Zeile 26: | Zeile 28: | ||
* Die Generierung des FE-Modells aus dem CAD-Modell erfolgt automatisiert. Die Berechnungsgenauigkeit kann dabei durch Parameter für die globale und lokale Vernetzungsdichte beeinflusst werden. | * Die Generierung des FE-Modells aus dem CAD-Modell erfolgt automatisiert. Die Berechnungsgenauigkeit kann dabei durch Parameter für die globale und lokale Vernetzungsdichte beeinflusst werden. | ||
In modernen CAD-Systemen ist die FEM für den Nichtspezialisten bereits soweit aufbereitet, dass er damit viele | In modernen CAD-Systemen ist die FEM für den Nichtspezialisten bereits soweit aufbereitet, dass er damit viele seiner alltäglichen Dimensionierungsprobleme weitestgehend lösen kann. | ||
"Nichtspezialist" für FEM bedeutet jedoch auch dann nicht, keinerlei Wissen über die Grundprinzipien und Fehlermöglichkeiten der FEM-Simulation besitzen zu müssen. Erforderlich sind folgende Grundkenntnisse: | "Nichtspezialist" für FEM bedeutet jedoch auch dann nicht, keinerlei Wissen über die Grundprinzipien und Fehlermöglichkeiten der FEM-Simulation besitzen zu müssen. Erforderlich sind folgende Grundkenntnisse: | ||
| Zeile 35: | Zeile 37: | ||
* Welche Probleme existieren bei der Darstellung und Interpretation der Simulationsergebnisse? | * Welche Probleme existieren bei der Darstellung und Interpretation der Simulationsergebnisse? | ||
Fehlt dieses erforderliche Grundwissen, so ist die Gefahr einer Fehlinterpretation der erhaltenen Ergebnisse sehr groß. Z.B. lässt sich die Richtigkeit der berechneten Belastungen und Verformungen komplexer Bauteile nur mit "gesundem Menschverstand" im Detail nicht immer überprüfen. | Fehlt dieses erforderliche Grundwissen, so ist die Gefahr einer Fehlinterpretation der erhaltenen Ergebnisse sehr groß. Z.B. lässt sich die Richtigkeit der berechneten Belastungen und Verformungen komplexer Bauteile nur mit "gesundem Menschverstand" im Detail nicht immer überprüfen. | ||
=== Simulationen in FEM-Systemen === | === Simulationen in FEM-Systemen === | ||
| Zeile 49: | Zeile 52: | ||
Neben der Bedienung des FEM-Systems sind nun umfangreichere Kenntnisse zur Methode der Finiten Elemente erforderlich: | Neben der Bedienung des FEM-Systems sind nun umfangreichere Kenntnisse zur Methode der Finiten Elemente erforderlich: | ||
<div align="right"> Bild: FEMAP mit NX-NASTRAN </div> | <div align="right"> Bild: FEMAP mit NX-NASTRAN </div> | ||
<div align="right"> Quelle: [http://www. | <div align="right"> Quelle: [http://www.plm.automation.siemens.com/de_de/products/nx/simulation/nastran/index.shtml '''Siemens PLM Software''']</div> | ||
[[Bild:Software_FEM_-_Tutorial_-_Einleitung_-_netz-beispiel.gif|right]] | [[Bild:Software_FEM_-_Tutorial_-_Einleitung_-_netz-beispiel.gif|right]] | ||
* Welche Modell-Elemente sind für das konkrete Problem geeignet? | * Welche Modell-Elemente sind für das konkrete Problem geeignet? | ||
Aktuelle Version vom 14. Februar 2020, 09:59 Uhr
Die Finite-Elemente-Methode (FEM) ist ein numerisches Verfahren zur näherungsweisen Lösung von partiellen Differentialgleichungen mit Randbedingungen.
Die Lösungen dieser partiellen Differentialgleichungen beschreiben die räumliche und auch zeitliche Verteilung der zugehörigen physikalischen Größen in einem betrachteten Raumgebiet. Man erhält im Ergebnis für das Innere eines räumlichen Objektes z.B.:
- mechanische Spannungen und Verformungen
- Drücke und Strömungen
- Temperaturen
- Verläufe elektrischer und magnetischer Felder
Damit kann man sowohl die Belastung des betrachteten Objekts als auch seine Wirkung auf die Umgebung berechnen. Deshalb ist die praktische Anwendung dieser Methode für Konstrukteure sehr interessant, wenn da nicht die Hürden der Mathematik wären! Leider führt fast jede Einführung zur FEM unweigerlich über die grundlegenden Vektordifferentialgleichungen und über die Verfahren ihrer numerischen Lösung. Das kann den Einsteiger schon etwas abschrecken!
FEM-Simulationen in CAD-Umgebungen
Zum Glück gehört die FEM zu den erfolgreichen Technologien. Wer heutzutage mit einem modernen CAD-System arbeitet, wird früher oder später die FEM nutzen, ohne etwas von FEM auf der Bedienoberfläche zu sehen. Sie verbirgt sich dabei z.B. unter dem Begriff "Belastungsanalyse" und bietet dem Konstrukteur nur die ihm geläufigen Fachbegriffe zur Konfiguration des "Belastungsexperiments", zur Durchführung der Simulation und zur Aufbereitung der Simulationsergebnisse.
Die Möglichkeiten solcher FEM-Simulationen innerhalb von CAD-Systemen sind im Vergleich zu FEM-Systemen zur Zeit noch begrenzt:
- Häufig nur für lineare Probleme, d.h. mit konstanten Materialkennwerten.
- Strukturmechanik, teilweise in Wechselwirkung mit Temperaturfeldern.
- Häufig schon Strömungsmechanik, zugeschnitten auf Spritzguss-Probleme.
- Kaum Möglichkeiten zur Nutzung unterschiedlicher Finite-Element-Typen.
- Die Generierung des FE-Modells aus dem CAD-Modell erfolgt automatisiert. Die Berechnungsgenauigkeit kann dabei durch Parameter für die globale und lokale Vernetzungsdichte beeinflusst werden.
In modernen CAD-Systemen ist die FEM für den Nichtspezialisten bereits soweit aufbereitet, dass er damit viele seiner alltäglichen Dimensionierungsprobleme weitestgehend lösen kann.
"Nichtspezialist" für FEM bedeutet jedoch auch dann nicht, keinerlei Wissen über die Grundprinzipien und Fehlermöglichkeiten der FEM-Simulation besitzen zu müssen. Erforderlich sind folgende Grundkenntnisse:
- Ist ein linearer Ansatz im Sinne der erforderlichen Genauigkeit überhaupt zulässig?
- Sind die Vereinfachungen bei der Definition der Randbedingungen (Lager, Kräfte usw.) zulässig?
- Welche geometrischen Details des CAD-Modells sind kritisch in Hinblick auf die Bildung eines FE-Modells?
- Welche Auswirkungen haben die Möglichkeiten zur FEM-Konfiguration?
- Welche Probleme existieren bei der Darstellung und Interpretation der Simulationsergebnisse?
Fehlt dieses erforderliche Grundwissen, so ist die Gefahr einer Fehlinterpretation der erhaltenen Ergebnisse sehr groß. Z.B. lässt sich die Richtigkeit der berechneten Belastungen und Verformungen komplexer Bauteile nur mit "gesundem Menschverstand" im Detail nicht immer überprüfen.
Simulationen in FEM-Systemen
In absehbarer Zukunft wird es immer FEM-Probleme geben, welche man mit den in CAD-Systemen "versteckten" FEM-Tools nicht lösen kann. Ein repräsentatives Beispiel sind die Belastungen von Zahnriemen unter verschiedensten Betriebsbedingungen:
- Die Materialeigenschaften des Zahnriemens sind Belastungs- und Richtungsabhängig. Es handelt sich deshalb um ein nichtlineares Problem.
- Die Randbedingungen (Eingriff der Zähne des Riemens in die Scheibe) sind abhängig von der Riemen-Verformung und dem Drehwinkel der Scheibe. Normale Lagerstellen können diese Abhängigkeiten nicht abbilden.
- Der im Riemen-Elastomer eingebettete Zugstrang erfordert spezielle Maßnahmen bei der Bildung des FE-Modells.
- Die Simulation der Getriebe-Bewegung erfordert eine Vielzahl einzelner FE-Simulationen mit schrittweise verändertem Drehwinkel der Riemenscheibe.
- ... und viele Probleme mehr!
In solchen Fällen hilft nur der Übergang vom CAD-System zu einem ausgereiftem FEM-System. Anstatt des CAD-Modells mit Geometrie- und Materialeigenschaften arbeitet man im FEM-Programm mit einem 2D- oder 3D-Netz Finiter Elemente.
Neben der Bedienung des FEM-Systems sind nun umfangreichere Kenntnisse zur Methode der Finiten Elemente erforderlich:

- Welche Modell-Elemente sind für das konkrete Problem geeignet?
- Welche Vereinfachungen der Geometrie sind erforderlich bzw. zulässig, um dass Problem überhaupt mit der FEM behandeln zu können?
- Wie sind die Randbedingungen definierbar?
- Wie ist das FE-Netz aufzubauen, damit in möglichst kurzer Zeit hinreichend genaue Ergebnisse berechnet werden?
- Wie ist mit der gleichen Zielstellung der Gleichungslöser zu konfigurieren?
- ...
Obwohl alle FEM-Systeme letztendlich mit einem FE-Netz arbeiten, bieten sie dem Anwender unterschiedlichste Benutzer-Oberflächen:
- Je universeller die Möglichkeiten eines FEM-Systems sind, desto stärker orientiert sich die Funktionalität an der Bearbeitung von FE-Netzen (Editieren von Knoten, Elementen, Subnetzen).
- Je spezialisierter ein FEM-System in Hinblick auf die physikalischen Domänen oder den Benutzerkreis ist, desto mehr orientiert sich die Funktionalität am Anwendungsbereich bzw. an der Benutzergruppe (Editieren von Geometrie, Benutzung fachspezifischer Begriffe, Tendenz zum automatisierten Vernetzen).
Wer mit FEM-Systemen simuliert, sollte über das erforderliche Erfahrungswissen in einer möglichst allgemeinen Form verfügen. Die Grundlage dafür bietet der verallgemeinerte FEM-Prozess auf Basis des FE-Netzes. Dann existieren erfahrungsgemäß auch kaum Probleme bei der Einarbeitung in ein neues FEM-System.
Entwicklung eigener Element-Typen
FEM-Systeme stellen Bibliotheken von Element-Typen für die FE-Netze bereit. Diese Element-Typen entstanden im Verlaufe von Jahren auf Grund unterschiedlichster Anforderungen der Nutzer (2D/3D-Probleme, Axialsymmetrische Probleme, diverse Belastungsfälle der Strukturmechanik usw.).
Neue Element-Typen benötigt man nur, wenn man ein neues Feldproblem bearbeitet, für das im FEM-System noch keine Element-Typen existieren. Dies könnte erforderlich sein, wenn man z.B. in Nanostrukturen mit ihren Quanteneffekten vorstößt. Erst dann benötigt man dafür die gesamte Theorie, die man in den so genannten Einführungen zur FEM erhält. Die numerische Umsetzung der theoretischen Grundlagen erfordert Tage- bis Monatelanges Programmieren, bis ein neuer Element-Typ funktioniert.
Der normale FEM-Nutzer wird mit diesen anspruchsvollen Aufgaben kaum konfrontiert werden. Solche Entwicklungen bleiben Spezialisten vorbehalten, die sowohl über das nötige theoretische Rüstzeug als auch über tiefgründige Erfahrungen im Umgang mit FEM-Systemen verfügen müssen.