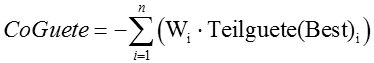Grundlagen: Optimierungsverfahren: Unterschied zwischen den Versionen
K (→Eltern-Anzahl) |
|||
| (34 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
Die Zielstellung für globale Suchverfahren der Optimierung besteht darin, innerhalb eines vorgegebenen Suchraums den absoluten Extremwert (das globale Optimum) zu finden. Bei der Anwendung innerhalb eines Entwurfsprozesses entspricht dies der absolut besten Lösung. D.h., es existiert keine Lösung, welche der idealen Lösung näher kommt: | Die Zielstellung für globale Suchverfahren der Optimierung besteht darin, innerhalb eines vorgegebenen Suchraums den absoluten Extremwert (das globale Optimum) zu finden. Bei der Anwendung innerhalb eines Entwurfsprozesses entspricht dies der absolut besten Lösung. D.h., es existiert keine Lösung, welche der idealen Lösung näher kommt: | ||
* Leider gibt es keine mathematischen oder numerischen [http://de.wikipedia.org/wiki/Optimierung_(Mathematik)#Methoden_der_globalen_nichtlinearen_Optimierung Methoden], welche für Suchräume mit mehr als 2-3 Entwurfsparametern das Finden der absolut besten Lösung garantieren können. Findet man einen Extremwert auf Gütefunktion, so weiß man praktisch nie, ob es nicht doch noch eine bessere Lösung gibt. | * Leider gibt es keine mathematischen oder numerischen [http://de.wikipedia.org/wiki/Optimierung_(Mathematik)#Methoden_der_globalen_nichtlinearen_Optimierung Methoden], welche für Suchräume mit mehr als 2-3 Entwurfsparametern das Finden der absolut besten Lösung garantieren können. Findet man einen Extremwert auf der Gütefunktion, so weiß man praktisch nie, ob es nicht doch noch eine bessere Lösung gibt. | ||
* Deshalb setzt man globale Suchverfahren innerhalb von Entwurfsprozessen meist "nur" zu Analysezwecken ein. Man verschafft sich damit einen "Überblick" über die Zielfunktion im einen zuvor definierten Suchraum: | * Deshalb setzt man globale Suchverfahren innerhalb von Entwurfsprozessen meist "nur" zu Analysezwecken ein. Man verschafft sich damit einen "Überblick" über die Zielfunktion im einen zuvor definierten Suchraum: | ||
** Innerhalb des Suchraums wird die Oberfläche der Zielfunktion in Form einzelner Abtastpunkte berechnet. | ** Innerhalb des Suchraums wird die Oberfläche der Zielfunktion in Form einzelner Abtastpunkte berechnet. | ||
| Zeile 14: | Zeile 14: | ||
**# sinnvolle Veränderung der Suchraums (Grenzen der Entwurfsparameter verschieben, erweitern oder einengen). | **# sinnvolle Veränderung der Suchraums (Grenzen der Entwurfsparameter verschieben, erweitern oder einengen). | ||
**# sinnvolle Positionen von Startpunkten für lokale Suchverfahren. | **# sinnvolle Positionen von Startpunkten für lokale Suchverfahren. | ||
* Ziel dieser Analyse ist das Ermitteln geeigneter Startpunkte für lokale Suchverfahren in einem sinnvoll definierten Suchraum. | * Ziel dieser Analyse ist das Ermitteln geeigneter Startpunkte für [[Grundlagen:_Optimierungsverfahren#Lokale_Suchverfahren|lokale Suchverfahren]] in einem sinnvoll definierten Suchraum. | ||
Bei der globalen Analyse der Zielfunktion hat man mit diversen Problemen zu kämpfen: | Bei der globalen Analyse der Zielfunktion hat man mit diversen Problemen zu kämpfen: | ||
* Der menschliche Blick auf mehrdimensionale Räume ist sehr eingeschränkt. So versagt bei mehr als 2 Entwurfsparametern recht schnell unsere Vorstellung. | * Der menschliche Blick auf mehrdimensionale Räume ist sehr eingeschränkt. So versagt bei mehr als 2 Entwurfsparametern recht schnell unsere Vorstellung. | ||
* Man kann immer nur endlich viele ausgewählte Punkte des Suchraums berechnen und muss die Zielfunktion dann hinein interpolieren. Sind die Abstände zwischen den Punkten zu groß, gehen die Details | * Man kann immer nur endlich viele ausgewählte Punkte des Suchraums berechnen und muss die Zielfunktion dann hinein interpolieren. Sind die Abstände zwischen den Punkten zu groß, gehen die Details verloren. | ||
Im Folgenden sollen die beiden Extrem-Beispiele für globale Suchverfahren dargestellt werden - das systematische Abtasten des Suchraumes ([http://de.wikipedia.org/wiki/Vollständiger_Versuchsplan Vollständiger Versuchsplan]) und das Erwürfeln zufälliger Lösungen im Suchraum ([http://de.wikipedia.org/wiki/Monte-Carlo-Simulation Monte Carlo Simulation]). Zwischen diesen beiden Extremen existiert eine Vielzahl von [http://de.wikipedia.org/wiki/Optimierung_(Mathematik)#Methoden_der_globalen_nichtlinearen_Optimierung heuristischen Methoden], um die Abtastungen auf erfolgversprechende Bereiche des Suchraums zu konzentrieren. | |||
=== Systematische Suche (Rastersuche) === | === Systematische Suche (Rastersuche) === | ||
| Zeile 28: | Zeile 30: | ||
* Das Verfahren der Rastersuche wird meist als Analyse-Werkzeug für die Eigenschaften einer Zielfunktion benutzt, um die Grundlage für den Einsatz lokaler Suchverfahren zu schaffen. | * Das Verfahren der Rastersuche wird meist als Analyse-Werkzeug für die Eigenschaften einer Zielfunktion benutzt, um die Grundlage für den Einsatz lokaler Suchverfahren zu schaffen. | ||
* Verfügt man über ein hinreichend schnell rechnendes Modell in einem kleinen Suchraum, kann man mit der Rastersuche natürlich auch iterativ recht schnell das mögliche Gebiet des globalen Optimums eingrenzen und dort sogar die exakte Position der bestmöglichen Lösung ermitteln: | * Verfügt man über ein hinreichend schnell rechnendes Modell in einem kleinen Suchraum, kann man mit der Rastersuche natürlich auch iterativ recht schnell das mögliche Gebiet des globalen Optimums eingrenzen und dort sogar die exakte Position der bestmöglichen Lösung ermitteln: | ||
*# Voraussetzung ist eine Zielfunktion,welche in großen Bereichen monoton ist und Optima in ausgeprägten breiten Tälern aufweist. | *# Voraussetzung ist eine Zielfunktion,welche in großen Bereichen [http://de.wikipedia.org/wiki/Monotonie_(Mathematik) monoton] ist und Optima in ausgeprägten breiten Tälern aufweist. | ||
*# Unter dieser Voraussetzung gilt dann unabhängig von der Anzahl der Entwurfsparameter, dass man wahrscheinlich ein Optimum umschlossen hat, wenn der beste Abtastwert kein Randpunkt ist. | *# Unter dieser Voraussetzung gilt dann unabhängig von der Anzahl der Entwurfsparameter, dass man wahrscheinlich ein Optimum umschlossen hat, wenn der beste Abtastwert kein Randpunkt ist. | ||
* Im Beispiel müsste man den Suchraum zu höheren Federkonstanten hin verschieben, um das globale Optimum zu umfassen. | * Im Beispiel müsste man den Suchraum zu höheren Federkonstanten '''''kFeder''''' hin verschieben, um das globale Optimum zu umfassen. | ||
Im obigen Diagramm wird nur die Gütefunktion "Zykluszeit" dargestellt, welche möglichst klein werden soll: | Im obigen Diagramm wird nur die Gütefunktion "Zykluszeit" dargestellt, welche möglichst klein werden soll: | ||
* Bei der Suche nach dem globalen Optimum muss man berücksichtigen, dass sich im abgetasteten Suchraum nur zulässige Lösungen befinden | * Bei der Suche nach dem globalen Optimum muss man berücksichtigen, dass sich im abgetasteten Suchraum nur zulässige Lösungen befinden (Wert der anhand der Restriktionen gebildeten Straf-Funktion = 0). | ||
* Damit existiert zusätzlich zu den Werten der Gütefunktion für jeden Abtastpunkt mit dem Wert der Straf-Funtion eine Information | * Damit existiert zusätzlich zu den Werten der Gütefunktion für jeden Abtastpunkt mit dem Wert der Straf-Funtion eine Information zum Grad der Restriktionsverletzung). | ||
* Der betrachtete Magnetantrieb soll mindestens eine Zykluszeit von 3,4 ms erreichen und seinen Bewegungsvorgang komplett ausführen:<div align="center"> [[Datei:Grundlagen_Optimierung_3d-Flaechen_Guete_und_Straffunktion.gif|.]] </div> | * Der betrachtete Magnetantrieb soll mindestens eine Zykluszeit von 3,4 ms erreichen und seinen Bewegungsvorgang komplett ausführen:<div align="center"> [[Datei:Grundlagen_Optimierung_3d-Flaechen_Guete_und_Straffunktion.gif|.]] </div> | ||
=== Monte-Carlo-Simulation === | === Monte-Carlo-Simulation === | ||
Oft kann infolge langsamer Modelle oder einer Vielzahl von Entwurfsparametern mittels Rastersuche keine sinnvolle Analyse der Zielfunktion erfolgen. Die erforderliche Berechnungszeit | Oft kann infolge langsamer Modelle oder einer Vielzahl von Entwurfsparametern mittels Rastersuche keine sinnvolle Analyse der Zielfunktion erfolgen. Die erforderliche Berechnungszeit wäre einfach zu groß:<div align="center"> [[Datei:Grundlagen_Optimierung_Monte_Carlo_Punkte.gif|.]] </div> | ||
* Dann | * Dann hilft die [http://de.wikipedia.org/wiki/Monte-Carlo-Simulation Monte-Carlo-Simulation] zumindest bei der Suche nach geeigneten Startpunkten für die lokale Suche: | ||
* Das Beispiel zeigt für den Magnetantrieb die Werte der Straffunktion ''StrafPkt'' in Abhängigkeit von Federkonstante ''cFeder'' und Ankerdurchmesser ''d_Anker'': | |||
* Das Beispiel zeigt für den Magnetantrieb die Werte der Straffunktion in Abhängigkeit von Federkonstante und Ankerdurchmesser: | ** Der Stern '''*''' kennzeichnet die beste "erwürfelte" Lösung (geeignet als Startpunkt für lokale Suche). | ||
** Der Stern * kennzeichnet die beste "erwürfelte" Lösung (Startpunkt für lokale Suche). | ** Die Ziffern 0…9 repräsentieren den Wertebereich der Straffunktion. | ||
** Die Ziffern repräsentieren den Wertebereich der Straffunktion. | ** Die anderen Symbole markieren Restriktionsverletzungen (z.B. '''u'''=überhöhte Spulenspannung / '''#'''=Mehrfach-Verletzungen)) | ||
** Die anderen Symbole markieren Restriktionsverletzungen (z.B. u=überhöhte Spulenspannung / #=Mehrfach-Verletzungen)) | |||
== Lokale Suchverfahren == | == Lokale Suchverfahren == | ||
Die Mehrzahl der verfügbaren Optimierungsverfahren sind Verfahren zur lokalen Suche: | Die Mehrzahl der verfügbaren Optimierungsverfahren sind Verfahren zur lokalen Suche: | ||
* [http://de.wikipedia.org/wiki/Nichtlineare_Optimierung#Methoden_der_lokalen_nichtlinearen_Optimierung_ohne_Nebenbedingungen Lokale Suchverfahren] sollen ausgehend von einem Startpunkt (Anfangslösung) möglichst das globale Optimum finden. In der Praxis wird jedoch nur ein lokales Minimum gefunden, welches vom Startpunkt aus durch schrittweise | * [http://de.wikipedia.org/wiki/Nichtlineare_Optimierung#Methoden_der_lokalen_nichtlinearen_Optimierung_ohne_Nebenbedingungen Lokale Suchverfahren] sollen ausgehend von einem Startpunkt (Anfangslösung) möglichst das globale Optimum finden. In der Praxis wird jedoch nur ein lokales Minimum gefunden, welches vom Startpunkt aus durch schrittweise Verbesserung der Lösung erreicht werden kann. | ||
* Das folgende Bild zeigt den möglichen Pfad eines lokalen Suchverfahrens auf der Zielfunktion "Zykluszeit" des Magnetantriebes: | * Das folgende Bild zeigt den möglichen Pfad eines lokalen Suchverfahrens auf der Zielfunktion "Zykluszeit" des Magnetantriebes: | ||
<div align="center"> [[Datei:Grundlagen_Optimierung_lokaler_Suchpfad.gif|.]] </div> | <div align="center"> [[Datei:Grundlagen_Optimierung_lokaler_Suchpfad.gif|.]] </div> | ||
| Zeile 57: | Zeile 57: | ||
* Dann tastet sich das lokale Suchverfahren entlang der Restriktionsgrenze auf der Zielfunktion, bis keine bessere Lösung entlang dieser Grenze gefunden werden kann. | * Dann tastet sich das lokale Suchverfahren entlang der Restriktionsgrenze auf der Zielfunktion, bis keine bessere Lösung entlang dieser Grenze gefunden werden kann. | ||
Zur Suche optimaler Lösungen für ein Entwurfsproblem eignen sich nur Methoden, welche keine analytische Ableitung der Zielfunktion benötigen: | Zur Suche optimaler Lösungen für ein Entwurfsproblem eignen sich meist nur Methoden, welche keine analytische Ableitung der Zielfunktion benötigen: | ||
* Die Zielfunktion in Entwurfsproblemen ist im Normalfall nicht als geschlossene Funktion gegeben. Sie ergibt sich nur punktuell durch Simulation einer konkreten Lösung im Suchraum der Entwurfsparameter. | * Die Zielfunktion in Entwurfsproblemen ist im Normalfall nicht als geschlossene Funktion gegeben. Sie ergibt sich nur punktuell durch Simulation einer konkreten Lösung im Suchraum der Entwurfsparameter. | ||
* Eventuell vom Suchverfahren benötigte 1.Ableitungen können an einem Punkt im Suchraum näherungsweise durch Abtastung als Differenzenquotient gewonnen werden. | * Eventuell vom Suchverfahren benötigte 1.Ableitungen können an einem Punkt im Suchraum näherungsweise durch Abtastung als Differenzenquotient gewonnen werden. | ||
* Besonders effektiv sind Verfahren, welche wie im Beispiel ausgehend vom Startpunkt sich in Richtung des steilsten Abstiegs bewegen. | * Besonders effektiv sind Verfahren, welche wie im Beispiel ausgehend vom Startpunkt sich in Richtung des steilsten Abstiegs bewegen. | ||
* Lokale Suchverfahren enden zwangsläufig, wenn sie auf dem Weg "nach | * Lokale Suchverfahren enden zwangsläufig, wenn sie auf dem Weg "nach unten" eine Mulde erreicht haben. Ursache ist das "blinde" Abtasten einzelner Punkte der Oberfläche in der näheren Umgebung mit dem Ziel, beim nächsten Schritt etwas tiefer zu kommen. Deshalb sollte der Startpunkt im Bereich eines vermuteten globalen Optimums liegen. | ||
* Klassische lokale Suchverfahren bewegen sich nur abwärts. Modernere Verfahren erlauben mit gewissen Wahrscheinlichkeiten auch eine Verschlechterung der Lösung, um aus kleineren Mulden wieder herauszufinden. | * Klassische lokale Suchverfahren bewegen sich nur abwärts. Modernere Verfahren erlauben mit gewissen Wahrscheinlichkeiten auch eine Verschlechterung der Lösung, um aus kleineren Mulden wieder herauszufinden. | ||
'''Abtastung der Zielfunktion mit Schrittweitenregelung (Beispiel "Hooke-Jeeves-Verfahren"):''' | '''Abtastung der Zielfunktion mit Schrittweitenregelung (Beispiel "Hooke-Jeeves-Verfahren"):''' | ||
* Die Wirkungsweise eines lokalen Suchverfahrens, welches die 1.Ableitung am aktuell erreichten Ort durch Abtastung der Zielfunktion ermittelt, soll am Beispiel des ''Hooke-Jeeves-Verfahrens'' erläutert werden. | |||
* Die Steigung der Zielfunktion am Punkt der aktuell erreichten Lösung wird über kleine Tastschritte ermittelt. Die genutzte Tastschrittweite muss dabei der Oberfläche der Zielfunktion angepasst sein. | * Die Steigung der Zielfunktion am Punkt der aktuell erreichten Lösung wird über kleine Tastschritte ermittelt. Die genutzte Tastschrittweite muss dabei der Oberfläche der Zielfunktion angepasst sein. | ||
* In Richtung des ermittelten steilsten Abstiegs wird anschließend ein größerer Schritt ausgeführt: | * In Richtung des ermittelten steilsten Abstiegs wird anschließend ein größerer Schritt ausgeführt:<div align="center"> [[Datei:Grundlagen_Optimierung__Pfad_Hooke_Jeeves.gif|.]] </div> | ||
<div align="center"> [[Datei:Grundlagen_Optimierung__Pfad_Hooke_Jeeves.gif|.]] </div> | |||
* Die Tastschritte werden gleichzeitig zur Verbesserung der Lösung genutzt. Beim Tastzyklus wird von einem Startvektor aus nacheinander in jede Koordinatenrichtung ein diskreter Suchzyklus durchgeführt. Führt dabei der Tastschritt in einer Richtung nicht zum Erfolg (Verbesserung des Gütewertes), so wird zusätzlich die entgegen gesetzte Richtung abgetastet. | * Die Tastschritte werden gleichzeitig zur Verbesserung der Lösung genutzt. Beim Tastzyklus wird von einem Startvektor aus nacheinander in jede Koordinatenrichtung ein diskreter Suchzyklus durchgeführt. Führt dabei der Tastschritt in einer Richtung nicht zum Erfolg (Verbesserung des Gütewertes), so wird zusätzlich die entgegen gesetzte Richtung abgetastet. | ||
* Nach einem Tastphase erfolgt die Extrapolation. In Richtung des ermittelten steilsten Abstieges wird ein größerer Schritt ausgeführt. Ein erneuter Extrapolationsschritt ist immer doppelt so groß wie der vorherige, solange dabei eine Verbesserung des Zielfunktionswertes erreicht wird. Schießt das Verfahren über den tiefsten Punkt hinaus oder in einen verbotenen Bereich, erfolgt eine schrittweise Verringerung der Extrapolationsschrittweite. | * Nach einem Tastphase erfolgt die Extrapolation. In Richtung des ermittelten steilsten Abstieges wird ein größerer Schritt ausgeführt. Ein erneuter Extrapolationsschritt ist immer doppelt so groß wie der vorherige, solange dabei eine Verbesserung des Zielfunktionswertes erreicht wird. Schießt das Verfahren über den tiefsten Punkt hinaus oder in einen verbotenen Bereich, erfolgt eine schrittweise Verringerung der Extrapolationsschrittweite. | ||
* Das Hooke-Jeeves-Verfahren regelt die anfängliche Tastschrittweite herunter, wenn längere Zeit keine Verbesserung des Zielfunktionswertes mehr erreicht werden konnte. Meist gelangt dann diese Schrittweite in Größenordnungen der stochastischen Rauigkeiten der Zielfunktion und das Optimierungsverfahren bleibt hängen, weil die partiellen Ableitungen total verfälscht werden (die reale Steigung wird nicht mehr erkannt). | * Das Hooke-Jeeves-Verfahren regelt die anfängliche Tastschrittweite herunter, wenn längere Zeit keine Verbesserung des Zielfunktionswertes mehr erreicht werden konnte. Meist gelangt dann diese Schrittweite in Größenordnungen der stochastischen Rauigkeiten der Zielfunktion und das Optimierungsverfahren bleibt hängen, weil die partiellen Ableitungen total verfälscht werden (die reale Steigung wird nicht mehr erkannt). | ||
'''Grenzen für den Einsatz lokaler Suchverfahren:''' | |||
* Der Einsatz ist problemlos möglich bei stetigen Zielfunktionen mit einem ausgeprägtem globalen Optimum, welches auf einem streng monotonen Pfad von jedem Punkt des Suchraums erreichbar ist, z.B.: | |||
<div align="center"> [[Datei:Grundlagen_Optimierung_Zielfunktion_glatt.gif|.]] </div> | |||
* Im Beispiel sind die '''Gesamtkosten z = Materialkosten + Verlustkosten''' für einen Hochstromleiter aus Kupfer zu minimieren. Gesucht sind Breite '''b''' und Höhe '''h''' für den optimalen Kupfer-Querschnitt. Die Kosten '''z''' wurden in obigem Diagramm wegen der Anschaulichkeit in der Form '''1/Ln(z)''' und gespiegelt dargestellt. Der Stern '''*''' des Optimums markiert also das globale Minimum, welches sich in einer gebogenen langen Mulde mit praktisch gleichberechtigten Lösungen befindet. | |||
* Existiert kein streng monotoner Pfad zum globalen Optimum (z.B. Stufen mit Gradient Null), so kann nur das lokale Minimum innerhalb der Stufe gefunden werden, auf welcher sich die Anfangslösung befand: | |||
<div align="center"> [[Datei:Grundlagen_Optimierung_Zielfunktion_Treppe.gif|.]] </div> | |||
* Klassische Verfahren der lokalen Suche versagen bei stark verrauschten Zielfunktionen, weil sie dann durch Abtastung der Umgebung fehlerhafte Informationen in Hinblick auf den Gradienten erhalten (Demo-Beispiel gewonnen durch Überlagerung einer Random-Funktion zur Zielfunktion des "Hochstromleiters"): | |||
<div align="center"> [[Datei:Grundlagen_Optimierung_Zielfunktion_verrauscht.gif|.]] </div> | |||
* Merkliches Rauschen entsteht bei der Gewinnung der Zielfunktionswerte mittels Messung oder durch die Nutzung instabiler numerischer Modelle. | |||
* Das immer vorhandene geringe Rauschen vieler Näherungsverfahren der numerischen Simulation bereitet erst Probleme, wenn die Abtastschrittweiten der lokalen Suchverfahren durch die automatische Schrittweitenregelung in die Größenordnung des Rauschanteils gelangen. Dies ist z.B. oft an Restriktionsgrenzen der Fall und verhindert dann die Konvergenz des Verfahrens. | |||
== Optimierung nach biologischem Vorbild == | == Optimierung nach biologischem Vorbild == | ||
| Zeile 216: | Zeile 229: | ||
* Mit der Zahl der Eltern muss proportional auch die Kinderzahl erhöht werden. Dies wird letztendlich durch die verfügbaren Ressourcen des Computers beschränkt. Bei rechenintensiven Simulationsmodellen wird z.B. die Rechenzeit für die Berechnung einer Generation so groß, dass dies durch den Fortschritt von Generation zu Generation nicht kompensiert wird. | * Mit der Zahl der Eltern muss proportional auch die Kinderzahl erhöht werden. Dies wird letztendlich durch die verfügbaren Ressourcen des Computers beschränkt. Bei rechenintensiven Simulationsmodellen wird z.B. die Rechenzeit für die Berechnung einer Generation so groß, dass dies durch den Fortschritt von Generation zu Generation nicht kompensiert wird. | ||
* Beginnend mit einer geringeren Elternanzahl kann man diese und die zugehörige Kinder-Anzahl durch Beobachtung des Fortschritts schrittweise anpassen, um möglichst schnell die optimale Lösung zu finden. | * Beginnend mit einer geringeren Elternanzahl kann man diese und die zugehörige Kinder-Anzahl durch Beobachtung des Fortschritts schrittweise anpassen, um möglichst schnell die optimale Lösung zu finden. | ||
'''Problem der 1. Eltern-Generation:''' | |||
# <u>ein Elter (lokales Suchverfahren):</u> | |||
#* Es wird die Anfangslösung sofort als 1. Eltern-Generation benutzt. | |||
#* Der Optimierungsverlauf entspricht einer lokalen Suche ausgehend von der Anfangslösung. | |||
#* Die generierten Kinder streuen ausgehend von den aktuellen Elter-Mutationsschrittweiten um das Elter. | |||
#* Die Mutationsschrittweiten passen sich im Verlaufe des Optimierungsfortschritts an den Gradienten der Zielfunktion an. | |||
# <u>mehrere Eltern (Start als globales Suchverfahren):</u> | |||
#* Die Anfangslösung (Startwerte) wird als ein Elter genutzt. | |||
#* Die Datensätze der zusätzlich benötigten Eltern werden im Suchraum im Sinne einer globalen Suche zufällig verteilt generiert. | |||
#* Beginnend mit diesen global verteilten Eltern der ersten Generation beginnt dann laut Konfiguration die ES mit der Generierung der Kinder und die Selektion der nächsten Eltern-Generation. | |||
#* Hierbei vergrößert sich die Gefahr, dass aus den weit von der Anfangslösung entfernt liegenden Eltern keine bewertbaren "Modell"-Kinder entstehen können. Ursachen sind z.B. physikalisch nicht realisierbare Exemplare bzw. aus Gründen der Modell-Stabilität numerisch nicht mehr berechenbaren Verhalten. | |||
#* Konvergiert die Lösung zu einem Optimum, so mündet der Prozess im Prinzip wieder in einer lokalen Suche. | |||
===== Kinder-Anzahl ===== | ===== Kinder-Anzahl ===== | ||
| Zeile 247: | Zeile 273: | ||
Ziel der Rekombination ist es, gute Eigenschaften verschiedener Eltern auf ein Kind zu übertragen: | Ziel der Rekombination ist es, gute Eigenschaften verschiedener Eltern auf ein Kind zu übertragen: | ||
* Es wurde mathematisch nachgewiesen, dass die Rekombination einen Anteil zur Fortschrittsgeschwindigkeit der ES beisteuert (Siehe: [http://www.bionik.tu-berlin.de/institut/skript/Fo10ES2.htm Rechenberg - Vorlesung Evolutionsstrategie II - Kapitel 5]) | * Es wurde mathematisch nachgewiesen, dass die Rekombination einen Anteil zur Fortschrittsgeschwindigkeit der ES beisteuert (Siehe: [http://www.bionik.tu-berlin.de/institut/skript/Fo10ES2.htm '''Rechenberg - Vorlesung Evolutionsstrategie II - Kapitel 5''']) | ||
* Ab zwei Eltern sollte die Multi-Rekombination angewandt werden, da die Rekombination der Datensätze aller Eltern immer einen größeren Evolutionsfortschritt bringt (in OptiY automatisch realisiert). | * Ab zwei Eltern sollte die Multi-Rekombination angewandt werden, da die Rekombination der Datensätze aller Eltern immer einen größeren Evolutionsfortschritt bringt (in OptiY automatisch realisiert). | ||
| Zeile 308: | Zeile 334: | ||
: '''1/5-Erfolgsregel''': | : '''1/5-Erfolgsregel''': | ||
:* Der Quotient aus den erfolgreichen Mutationen (also Mutationen, die eine Verbesserung der Fitness bewirken) zu allen Mutationen sollte etwa ein Fünftel betragen. | :* Der Quotient aus den erfolgreichen Mutationen (also Mutationen, die eine Verbesserung der Fitness bewirken) zu allen Mutationen sollte etwa ein Fünftel betragen. Dann befindet sich der Evolutionsprozess im Evolutionsfenster. | ||
:* Diese Regel kann die Grundlage für eine Anpassung der Mutationsschrittweite bilden. Ist der Quotient >1/5, so sollte die Varianz der Mutationen erhöht werden, bei einem kleineren Quotienten sollte sie verringert werden. | :* Diese Regel kann die Grundlage für eine Anpassung der Mutationsschrittweite bilden. Ist der Quotient >1/5, so sollte die Varianz der Mutationen erhöht werden, bei einem kleineren Quotienten sollte sie verringert werden. | ||
:* Infolge der Einbeziehung der Mutationsschrittweite in den Optimierungsprozess stellt sich diese automatisch so ein, dass sich der Prozess innerhalb des Evolutionsfensters befindet. | |||
=== Co-Evolutionaere Strategien === | |||
Die Prinzipien der Evolutionsstrategien sind auch nutzbar, um Problemstellungen der [[Grundlagen:_Optimierung#Mehrkriterien-Optimierung|Mehrkriterien-Optimierung]] zu lösen, wie sie in den [[Grundlagen:_Optimierung|Grundlagen zur Optimierung]] beschrieben sind: | |||
<div align="center"> [[Datei:Software_SimX_-_Nadelantrieb_-_Robust-Optimierung_-_paretomenge.gif|.]] </div> | |||
Das grundlegende Konzept co-evolutionärer Algorithmen basiert auf Ökosystemen mit stark [http://de.wikipedia.org/wiki/Populationsdynamik wechselwirkenden Populationen] verschiedener Arten ([http://de.wikipedia.org/wiki/Coevolution Coevolution]): | |||
* Co-Evolution ist der Antrieb für die ständige Weiterentwicklung der Arten innerhalb von Ökosystemen auch bei stabilen Umweltbedingungen. | |||
* Die Prinzipien der Co-Evolution kann man für die Mehrkriterien-Optimierung nutzen, indem man die normale Evolutionsstrategie erweitert. | |||
* Dazu wird speziell die wechselseitige Anpassung von [http://de.wikipedia.org/wiki/Lotka-Volterra-Gleichung Räuber- und Beutetieren] nachgebildet (schnellere Hasen sind von Nachteil für die Füchse und umgekehrt): | |||
** Der Wettbewerb existiert nicht nur innerhalb einer Art, sondern auch zwischen den co-existierenden Arten. | |||
** In den Fitnesswert eines Individuums muss auch die Fitness der jeweils anderen Art einfließen - die Räuber-Fitness wächst mit verminderter Beute-Fitness und umgekehrt. | |||
<div align="center"> | Ein Kunstgriff zur Nutzung der Co-Evolution für die Mehrkriterien-Optimierung kann darin bestehen, die Gewichtungsfaktoren der Teilgüten als Optimierungsvariablen der sogenannten Co-Individuen zu definieren: | ||
* '''Beutetiere:''' Individuen (Parametersätze) der aktuellen Population von Lösungen. | |||
* '''Räuber:''' Zusätzliche Population von Co-Individuen, welche die wertende Sicht der Nutzer auf die zu optimierende Lösung verkörpern: | |||
** Die Gewichtsfaktoren der Teilgüten stellen die Optimierungsvariablen der Räuber dar. | |||
** Diese Gewichtsfaktoren können sich damit ausgehend von einem vorgegebenen Anfangswert durch die Evolutionsstrategie verändern. | |||
** Die Summe aller Gewichtungsfaktoren jedes Räubers bleibt konstant =1 (Randbedingung). | |||
* Die Gesamt-Güte jeder Lösung ("Beutetier") wird durch die benutzten Gewichtsfaktoren für die Teilgüten bestimmt. Die Güte einer Lösung ist also Nutzerabhängig, da jeder Nutzer ("Räuber") eigene Gewichtsfaktoren besitzt: | |||
<div align="center"> [[Datei:Grundlagen_Optimierung_Gesamtguete_mit_Wichtung.gif|.]] </div> | |||
* Um an alle Lösungen (Individuen) einen einheitlichen Maßstab anzulegen, werden die Gewichtsfaktoren des besten Co-Individuums (der vorherigen Generation) benutzt. Damit widerspiegelt die berechnete Fitness der aktuellen Lösungen die Anpassung an den bisherigen besten Räuber: | |||
<div align="center"> [[Datei:Grundlagen_Optimierung_Guete_mit_Wichtung-co-best.gif|.]] </div> | |||
* Der Fitness-Wert eines Co-Individuums ("Räubers") wird mittels seiner eigenen Gewichtsfaktoren und den Teilgüten des besten Individuums (beste Lösung der vorherigen Generation) berechnet: | |||
<div align="center"> [[Datei:Grundlagen_Optimierung_Co-Guete_mit_Wichtung-best.gif|.]] </div> | |||
* Ein Räuber ist umso besser, je schlechter in Hinblick auf seine Eigenschaften (W<sub>i</sub>) die zur Zeit bestangepasste Beute erscheint. Dies widerspiegelt sich im negativen Vorzeichen nach der Summenbildung. | |||
* Der Bezug auf die vorherige Generation erfolgt aus Vereinfachungsgründen, weil sich die Fitness-Werte innerhalb der aktuellen Generation wechselseitig bedingen. | |||
* Die Population der Lösungen ("Beutetiere") driftet zur Pareto-Menge. Die unterlegte "normale" Evolutionsstrategie bevorzugt Lösungen in Richtung dieser Pareto-Menge. | |||
* Das Prinzip der wechselseitigen Anpassung zwischen Individuen und Co-Individuen führt zu endlosen Schwingungen entlang der Pareto-Menge. | |||
''' | '''''Hinweis:''''' Im OptiY ist ein abgewandelter Algorithmus implementiert! | ||
Aktuelle Version vom 11. Oktober 2019, 14:40 Uhr
Globale Suchverfahren
Zielstellung
Die Zielstellung für globale Suchverfahren der Optimierung besteht darin, innerhalb eines vorgegebenen Suchraums den absoluten Extremwert (das globale Optimum) zu finden. Bei der Anwendung innerhalb eines Entwurfsprozesses entspricht dies der absolut besten Lösung. D.h., es existiert keine Lösung, welche der idealen Lösung näher kommt:
- Leider gibt es keine mathematischen oder numerischen Methoden, welche für Suchräume mit mehr als 2-3 Entwurfsparametern das Finden der absolut besten Lösung garantieren können. Findet man einen Extremwert auf der Gütefunktion, so weiß man praktisch nie, ob es nicht doch noch eine bessere Lösung gibt.
- Deshalb setzt man globale Suchverfahren innerhalb von Entwurfsprozessen meist "nur" zu Analysezwecken ein. Man verschafft sich damit einen "Überblick" über die Zielfunktion im einen zuvor definierten Suchraum:
- Innerhalb des Suchraums wird die Oberfläche der Zielfunktion in Form einzelner Abtastpunkte berechnet.
- Man sollte versuchen, daraus die Eigenschaften der Zielfunktion zu erkennen:
- Vorhandensein lokaler Optima, Unstetigkeitsstellen,
- mögliche Position des globalen Optimums,
- sinnvolle Veränderung der Suchraums (Grenzen der Entwurfsparameter verschieben, erweitern oder einengen).
- sinnvolle Positionen von Startpunkten für lokale Suchverfahren.
- Ziel dieser Analyse ist das Ermitteln geeigneter Startpunkte für lokale Suchverfahren in einem sinnvoll definierten Suchraum.
Bei der globalen Analyse der Zielfunktion hat man mit diversen Problemen zu kämpfen:
- Der menschliche Blick auf mehrdimensionale Räume ist sehr eingeschränkt. So versagt bei mehr als 2 Entwurfsparametern recht schnell unsere Vorstellung.
- Man kann immer nur endlich viele ausgewählte Punkte des Suchraums berechnen und muss die Zielfunktion dann hinein interpolieren. Sind die Abstände zwischen den Punkten zu groß, gehen die Details verloren.
Im Folgenden sollen die beiden Extrem-Beispiele für globale Suchverfahren dargestellt werden - das systematische Abtasten des Suchraumes (Vollständiger Versuchsplan) und das Erwürfeln zufälliger Lösungen im Suchraum (Monte Carlo Simulation). Zwischen diesen beiden Extremen existiert eine Vielzahl von heuristischen Methoden, um die Abtastungen auf erfolgversprechende Bereiche des Suchraums zu konzentrieren.
Systematische Suche (Rastersuche)
Die N Achsen der Entwurfsparameter werden innerhalb des Suchraums in gleichmäßige Abstände geteilt. Die Schnittpunkte der Rasterlinien definieren die Abtastpunkte auf der Oberfläche der Zielfunktion.
In der statistischen Versuchsplanung (design of experiments = DoE) ist dieses Verfahren auch als vollständiger Versuchsplan (full factorial design) bekannt:
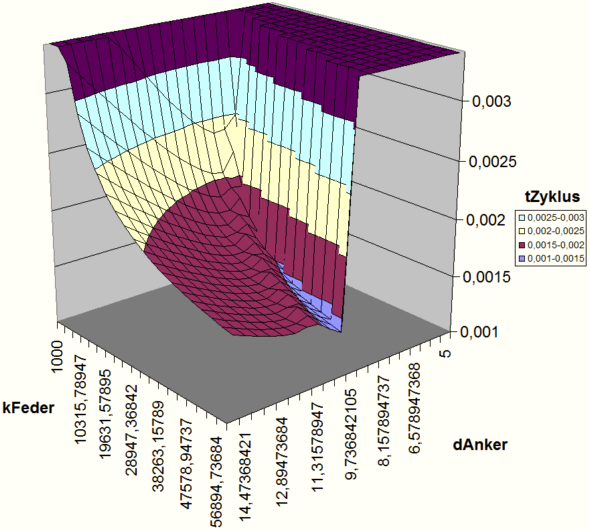
- Im obigen Beispiel wurde für einen Elektromagneten die Zykluszeit in Abhängigkeit vom Ankerdurchmesser und der Rückholfeder untersucht.
- Das Verfahren der Rastersuche wird meist als Analyse-Werkzeug für die Eigenschaften einer Zielfunktion benutzt, um die Grundlage für den Einsatz lokaler Suchverfahren zu schaffen.
- Verfügt man über ein hinreichend schnell rechnendes Modell in einem kleinen Suchraum, kann man mit der Rastersuche natürlich auch iterativ recht schnell das mögliche Gebiet des globalen Optimums eingrenzen und dort sogar die exakte Position der bestmöglichen Lösung ermitteln:
- Voraussetzung ist eine Zielfunktion,welche in großen Bereichen monoton ist und Optima in ausgeprägten breiten Tälern aufweist.
- Unter dieser Voraussetzung gilt dann unabhängig von der Anzahl der Entwurfsparameter, dass man wahrscheinlich ein Optimum umschlossen hat, wenn der beste Abtastwert kein Randpunkt ist.
- Im Beispiel müsste man den Suchraum zu höheren Federkonstanten kFeder hin verschieben, um das globale Optimum zu umfassen.
Im obigen Diagramm wird nur die Gütefunktion "Zykluszeit" dargestellt, welche möglichst klein werden soll:
- Bei der Suche nach dem globalen Optimum muss man berücksichtigen, dass sich im abgetasteten Suchraum nur zulässige Lösungen befinden (Wert der anhand der Restriktionen gebildeten Straf-Funktion = 0).
- Damit existiert zusätzlich zu den Werten der Gütefunktion für jeden Abtastpunkt mit dem Wert der Straf-Funtion eine Information zum Grad der Restriktionsverletzung).
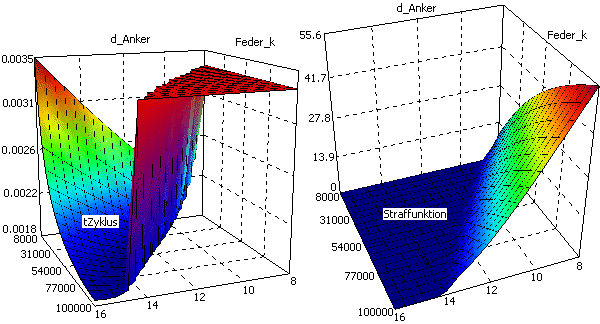
- Der betrachtete Magnetantrieb soll mindestens eine Zykluszeit von 3,4 ms erreichen und seinen Bewegungsvorgang komplett ausführen:
Monte-Carlo-Simulation
Oft kann infolge langsamer Modelle oder einer Vielzahl von Entwurfsparametern mittels Rastersuche keine sinnvolle Analyse der Zielfunktion erfolgen. Die erforderliche Berechnungszeit wäre einfach zu groß:
- Dann hilft die Monte-Carlo-Simulation zumindest bei der Suche nach geeigneten Startpunkten für die lokale Suche:
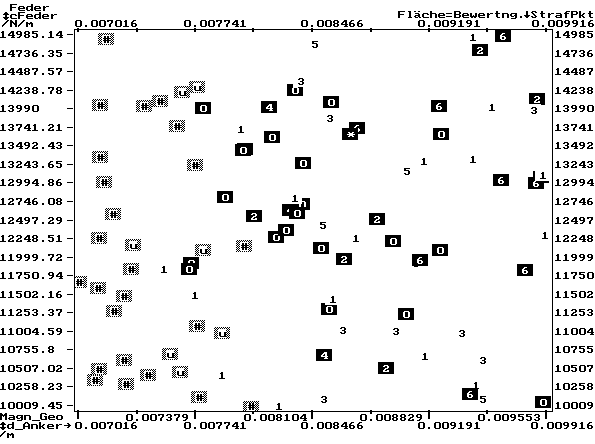
- Das Beispiel zeigt für den Magnetantrieb die Werte der Straffunktion StrafPkt in Abhängigkeit von Federkonstante cFeder und Ankerdurchmesser d_Anker:
- Der Stern * kennzeichnet die beste "erwürfelte" Lösung (geeignet als Startpunkt für lokale Suche).
- Die Ziffern 0…9 repräsentieren den Wertebereich der Straffunktion.
- Die anderen Symbole markieren Restriktionsverletzungen (z.B. u=überhöhte Spulenspannung / #=Mehrfach-Verletzungen))
Lokale Suchverfahren
Die Mehrzahl der verfügbaren Optimierungsverfahren sind Verfahren zur lokalen Suche:
- Lokale Suchverfahren sollen ausgehend von einem Startpunkt (Anfangslösung) möglichst das globale Optimum finden. In der Praxis wird jedoch nur ein lokales Minimum gefunden, welches vom Startpunkt aus durch schrittweise Verbesserung der Lösung erreicht werden kann.
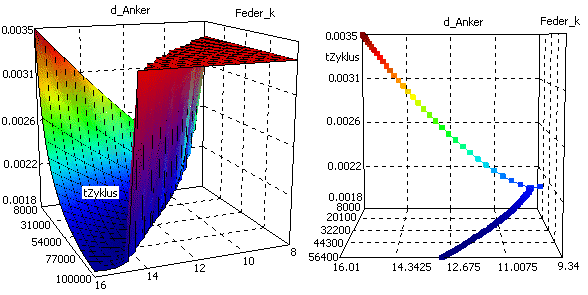
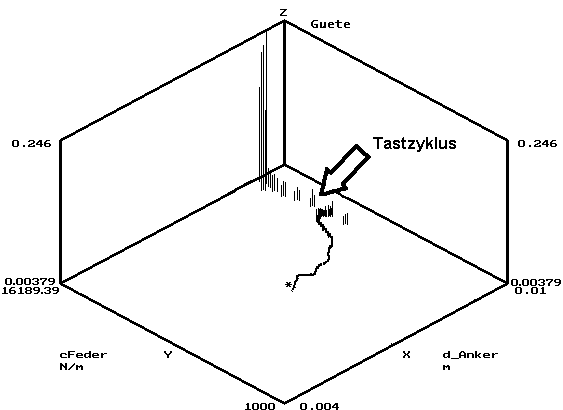
- Das folgende Bild zeigt den möglichen Pfad eines lokalen Suchverfahrens auf der Zielfunktion "Zykluszeit" des Magnetantriebes:
- Es erfolgt im Beispiel eine stetige Verbesserung der Zykluszeit entlang des "steilsten Abstiegs", bis die Lösung nicht mehr alle Forderungen erfüllt.
- Dann tastet sich das lokale Suchverfahren entlang der Restriktionsgrenze auf der Zielfunktion, bis keine bessere Lösung entlang dieser Grenze gefunden werden kann.
Zur Suche optimaler Lösungen für ein Entwurfsproblem eignen sich meist nur Methoden, welche keine analytische Ableitung der Zielfunktion benötigen:
- Die Zielfunktion in Entwurfsproblemen ist im Normalfall nicht als geschlossene Funktion gegeben. Sie ergibt sich nur punktuell durch Simulation einer konkreten Lösung im Suchraum der Entwurfsparameter.
- Eventuell vom Suchverfahren benötigte 1.Ableitungen können an einem Punkt im Suchraum näherungsweise durch Abtastung als Differenzenquotient gewonnen werden.
- Besonders effektiv sind Verfahren, welche wie im Beispiel ausgehend vom Startpunkt sich in Richtung des steilsten Abstiegs bewegen.
- Lokale Suchverfahren enden zwangsläufig, wenn sie auf dem Weg "nach unten" eine Mulde erreicht haben. Ursache ist das "blinde" Abtasten einzelner Punkte der Oberfläche in der näheren Umgebung mit dem Ziel, beim nächsten Schritt etwas tiefer zu kommen. Deshalb sollte der Startpunkt im Bereich eines vermuteten globalen Optimums liegen.
- Klassische lokale Suchverfahren bewegen sich nur abwärts. Modernere Verfahren erlauben mit gewissen Wahrscheinlichkeiten auch eine Verschlechterung der Lösung, um aus kleineren Mulden wieder herauszufinden.
Abtastung der Zielfunktion mit Schrittweitenregelung (Beispiel "Hooke-Jeeves-Verfahren"):
- Die Wirkungsweise eines lokalen Suchverfahrens, welches die 1.Ableitung am aktuell erreichten Ort durch Abtastung der Zielfunktion ermittelt, soll am Beispiel des Hooke-Jeeves-Verfahrens erläutert werden.
- Die Steigung der Zielfunktion am Punkt der aktuell erreichten Lösung wird über kleine Tastschritte ermittelt. Die genutzte Tastschrittweite muss dabei der Oberfläche der Zielfunktion angepasst sein.
- In Richtung des ermittelten steilsten Abstiegs wird anschließend ein größerer Schritt ausgeführt:
- Die Tastschritte werden gleichzeitig zur Verbesserung der Lösung genutzt. Beim Tastzyklus wird von einem Startvektor aus nacheinander in jede Koordinatenrichtung ein diskreter Suchzyklus durchgeführt. Führt dabei der Tastschritt in einer Richtung nicht zum Erfolg (Verbesserung des Gütewertes), so wird zusätzlich die entgegen gesetzte Richtung abgetastet.
- Nach einem Tastphase erfolgt die Extrapolation. In Richtung des ermittelten steilsten Abstieges wird ein größerer Schritt ausgeführt. Ein erneuter Extrapolationsschritt ist immer doppelt so groß wie der vorherige, solange dabei eine Verbesserung des Zielfunktionswertes erreicht wird. Schießt das Verfahren über den tiefsten Punkt hinaus oder in einen verbotenen Bereich, erfolgt eine schrittweise Verringerung der Extrapolationsschrittweite.
- Das Hooke-Jeeves-Verfahren regelt die anfängliche Tastschrittweite herunter, wenn längere Zeit keine Verbesserung des Zielfunktionswertes mehr erreicht werden konnte. Meist gelangt dann diese Schrittweite in Größenordnungen der stochastischen Rauigkeiten der Zielfunktion und das Optimierungsverfahren bleibt hängen, weil die partiellen Ableitungen total verfälscht werden (die reale Steigung wird nicht mehr erkannt).
Grenzen für den Einsatz lokaler Suchverfahren:
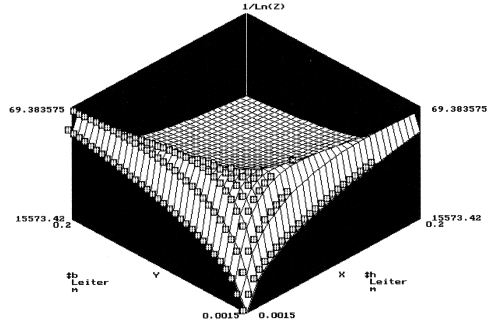
- Der Einsatz ist problemlos möglich bei stetigen Zielfunktionen mit einem ausgeprägtem globalen Optimum, welches auf einem streng monotonen Pfad von jedem Punkt des Suchraums erreichbar ist, z.B.:
- Im Beispiel sind die Gesamtkosten z = Materialkosten + Verlustkosten für einen Hochstromleiter aus Kupfer zu minimieren. Gesucht sind Breite b und Höhe h für den optimalen Kupfer-Querschnitt. Die Kosten z wurden in obigem Diagramm wegen der Anschaulichkeit in der Form 1/Ln(z) und gespiegelt dargestellt. Der Stern * des Optimums markiert also das globale Minimum, welches sich in einer gebogenen langen Mulde mit praktisch gleichberechtigten Lösungen befindet.
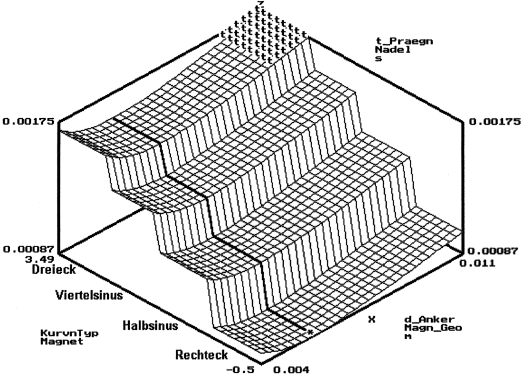
- Existiert kein streng monotoner Pfad zum globalen Optimum (z.B. Stufen mit Gradient Null), so kann nur das lokale Minimum innerhalb der Stufe gefunden werden, auf welcher sich die Anfangslösung befand:
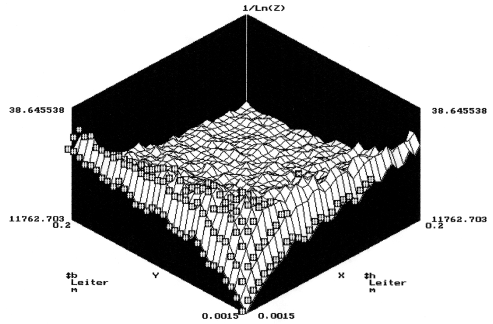
- Klassische Verfahren der lokalen Suche versagen bei stark verrauschten Zielfunktionen, weil sie dann durch Abtastung der Umgebung fehlerhafte Informationen in Hinblick auf den Gradienten erhalten (Demo-Beispiel gewonnen durch Überlagerung einer Random-Funktion zur Zielfunktion des "Hochstromleiters"):
- Merkliches Rauschen entsteht bei der Gewinnung der Zielfunktionswerte mittels Messung oder durch die Nutzung instabiler numerischer Modelle.
- Das immer vorhandene geringe Rauschen vieler Näherungsverfahren der numerischen Simulation bereitet erst Probleme, wenn die Abtastschrittweiten der lokalen Suchverfahren durch die automatische Schrittweitenregelung in die Größenordnung des Rauschanteils gelangen. Dies ist z.B. oft an Restriktionsgrenzen der Fall und verhindert dann die Konvergenz des Verfahrens.
Optimierung nach biologischem Vorbild
Einfuehrung
Die natürliche Evolution der Lebewesen hat erstaunliche Lösungen für das Funktionieren von Organismen in unterschiedlichsten ökologischen Nischen hervorgebracht. Die einzelnen Arten von Lebewesen stellen offensichtlich optimierte Lösungen für das Überleben in ihrer jeweiligen Umwelt dar.
Schon sehr früh haben Menschen begonnen, "Lösungen" der Natur auf die Technik zu übertragen. Das älteste dokumentierte Beispiel der systematischen Übertragung solcher Natur-Phänomene auf technische Objekte ist Leonardo da Vincis Idee, den Vogelflug auf Flugapparate zu übertragen. Seit ca. 1/2 Jahrhundert fasst man solche Bestrebungen unter dem Begriff Bionik zusammen.
Die sogenannten evolutionären Algorithmen sind eine Klasse von Optimierungsverfahren, deren Funktionsweise von der Evolution der Lebewesen inspiriert wurde. Ausgangspunkt für die Entwicklung von evolutionären Algorithmen ist eine Abstraktion der realen natürlichen Evolution auf das Grundprinzip ihrer Wirkungsweise.
Grundprinzip:
- Evolutionäre Algorithmen erzeugen aus einer Elterngeneration (von Parametersätzen) durch die genetischen Prozeduren (Mutation, Rekombination) eine Kindergeneration. Eine Teilmenge der Kinder wird nach Fitness-Selektion (anhand des Verhaltens) zur neuen Elterngeneration.
- Die Parameter der genetischen Prozeduren sind selbst Bestandteil der Optimierung (Mutationsraten, Art der Rekombination).
- Voraussetzung der Anwendung evolutionärer Verfahren auf ein System (z.B. Zielfunktion) ist, dass dieses eine hinreichende Kausalität zwischen Ursachen (Parameteränderungen) und Wirkungen (Verhaltensänderungen) vermittelt.
Analogiebeziehungen "Natur - Technik":
- Individuum: Anstatt eines lebenden Organismus wird von den evolutionären Algorithmen ein numerisches Modell des zu optimierenden Objektes benutzt.
- Population: Die Vielzahl von Individuen einer Art wird durch unterschiedliche Parametersätze eines numerischen Modells abgebildet.
- Genotyp: Der genetische Code eines Individuums (ATGC-Basen in DNA bzw. RNA) wird durch den binären Code des Modells repräsentiert (Modell-Parameter und -Algorithmen).
- Phänotyp: Das einzelne Individuum entsteht auf der Basis von Strukturbildungsprozessen ausgehend vom Genotyp in einer geeigneten Umgebung. Das konkrete Modellverhalten als Analogie zum Phänotyp entsteht im Prozess der Simulation des parametrisierten Modells in einer geeigneten Hard- und Software-Umgebung.
- Fortpflanzung: die Erzeugung von Kind-Genotypen mittels Rekombination und Mutation wird abgebildet durch Varianten-Generierung mittels genetischer Operatoren angewandt auf die Optimierungsvariablen als Teilmenge eines Parametersatzes.
- Selektion: In der Natur erfolgt die Selektion anhand des Fortpflanzungserfolges (Fitness) der Kind-Phänotypen. Dies entspricht der Varianten-Reduktion auf Basis der für die unterschiedlichen Parametersätze berechneten Zielfunktionswerte.
Genetische Algorithmen und Evolutionsstrategien
Die Entwicklung universeller Optimierungsverfahren nach dem Grundprinzip der natürlichen Evolution verlief seit den 1960-er Jahren in den USA und Deutschland in zwei unterschiedliche Richtungen:
1. Genetische Algorithmen (GA)
Dieser Typ von evolutionären Algorithmen wurde bekannt durch die Arbeiten der US-Amerikaner Holland und Goldberg. Die GA versuchen das biologische Vorbild möglichst 1:1 nachzubilden:
- Das Bit ist in Analogie zu den Nuklein-Basen die grundlegende Einheit für das Wirken der genetischen Operatoren:
- Problematisch ist die Aufbereitung des Modells und seiner Parameter zur Erzielung einer hinreichend starken Kausalität zwischen Parameter- und Verhaltensänderung.
- So ist z.B. die klassische binäre Codierung von reellen Zahlen als Gleitkommazahlen mit Exponent und Mantisse sehr ungünstig, da Änderungen von Bits im Exponenten unverhältnismäßig große Auswirkungen auf den Wert der Zahl besitzen.
- Mutation bewirkt das "Umklappen" von Bits in der Problem-Repräsentation entsprechend vorgegebener Wahrscheinlichkeiten:
- Nachgebildet wird damit die Ursache von Mutationen im Sinne des Austauschs von Nuklein-Basen im Genotyp:
- Die Veränderung einzelner Bit kann in Abhängigkeit von der Bit-Position in der Problem-Repräsentation zu extrem unterschiedlichen Verhaltensänderungen des Modells führen (von praktisch unmerklich bis katastrophal).
- Die extremen Verhaltensänderungen ermöglichen freie Sprünge innerhalb des Suchraums. Damit können mit geringer Wahrscheinlichkeit auch Lösungen gefunden werden, welche durch stetige Verbesserung einer vorhandenen Lösung nicht erreichbar sind.
- Anwendungsschwerpunkt der GA ist deshalb die Strukturoptimierung (ein Bit verkörpert z.B. eine Relation zwischen zwei Komponenten).
- Rekombination erfolgt nach dem Schema der Natur (dominant bzw. rezessiv).
Dieser Typ von evolutionären Algorithmen wurde vor allem durch die Arbeiten von Schwefel und Rechenberg an der TU Berlin entwickelt. Die ES versucht, die Wirkung der natürlichen Evolution auf einem höheren Abstraktionsniveau nachzubilden, als die GA:
- Die reelle Zahl ist die grundlegende Einheit für das Wirken der genetischen Operatoren:
- Geometrisch-stoffliche Parameter technischer Objekte können meist problemlos in Form reeller Zahlen repräsentiert werden.
- Das ist günstig für eine starken Kausalität zwischen Parameter- und Verhaltensänderung.
- Anwendungsschwerpunkt der ES ist deshalb die Parameteroptimierung für vorgegebene Systemstrukturen.
- Mutation bewirkt eine Zufallswahl aus einer Verteilungsfunktion um den aktuellen Wert der reell-wertigen Optimierungsvariablen:
- Die durch Mutation erzeugten Parametersätze der Kindergeneration befinden sich auf der Zielfunktion immer in der Nähe der Elterngeneration (Diffusion anstatt Fluktuation).
- ES finden im Unterschied zu GA ausgehend von einer Anfangslösung nur Optima, welche überwiegend durch kontinuierliche Verbesserungen erreichbar sind. Die ES kann deshalb meist nicht den gesamten Suchraum erkunden.
- Rekombination bewirkt eine gewichtete Mittelwertbildung aus beteiligten Optimierungsvariablen. Die kombinierten Parameter der Kinder liegen mit ihren Werten zwischen denen der an der Rekombination beteiligten Eltern.
Grundlagen zu den Evolutionsstrategien (ES)
Anwendungsbereich
Im Weiteren wird hier nur die ES vertieft betrachtet, weil Sie für ingenieurtechnische Optimierungen im Vergleich zu den genetischen Algorithmen (GA) einfacher und anschaulicher zu nutzen ist:
- Da die ES eine direkte Problem-Präsentation in Form z.B. der reellen Zahlen benutzt, entfällt eine aufwändige Transformation für die Parameter-Optimierung bei vergebener Struktur des zu optimierenden Systems.
- Der Optimierungsfortschritt ist für den menschlichen Beobachter als Driften einer Lösungsmenge auf der Zielfunktion zum Optimum nachvollziehbar, da chaotische Fluktuationen der Lösungen nicht stattfinden bzw. schnell eliminiert werden.
Die ES wurden ursprünglich entwickelt für die Optimierung mit verrauschter Zielfunktion bei Messungen am realen Objekt:
- Damit bewältigen die ES auch das Rauschen numerischer Modelle infolge Rundungs- und Approximationsfehler der numerischen Lösung.
- Die ES konvergieren über vereinzelte Unstetigkeitsstellen hinweg, wenn global im Suchraum hinreichend starke Kausalität besteht (ähnliche Ursachen führen zu ähnlichen Wirkungen).
- Sie sind einsetzbar in Suchräumen, bei denen auf Grund der Mächtigkeit (Zahl der Optimierungsvariablen) klassische Verfahren versagen.
Auch ES können keine Wunder vollbringen und besitzen Grenzen bei der Anwendung:
- Zielfunktionen mit vielen lokalen Optima verhindern meist das Finden des globalen Optimums.
- Ist die Kausalität zu schwach, "zerfällt" die Lösung, indem es zu keiner Konvergenz kommt.
- Bei wenigen Optimierungsvariablen und hinreichend glatten (nicht verrauschten) Zielfunktionen ohne Unstetigkeitsstellen sind klassische Gradienten- und Abtastverfahren besser geeignet. Es lohnt sich deshalb, Aufwand in die Realisierung einer "glatten" Zielfunktion zu investieren!
Notation von Evolutionsstrategien
Die folgenden Schreibweisen wurde von H.-P. Schwefel in seiner Dissertation 1975 eingeführt:
+ (µ λ) - Basisalgorithmus der Evolutionsstrategie ,
- µ Eltern erzeugen in willkürlicher Folge
- λ mutierte Nachkommen.
- Komma:
- die Eltern sterben sofort nach der "Fortpflanzung"
- nur Nachkommen werden nach der Selektion zu Eltern einer neuen Generation
- der erreichte Zielfunktionswert kann sich dadurch auch verschlechtern
- Plus:
- auch die Eltern nehmen gleichberechtigt mit den Nachkommen an der Selektion für die nächste Generation teil
- es können theoretisch (und praktisch) unsterbliche Eltern entstehen
Beispiele:
- (1+1)-ES :
- einfachste Evolutionsstrategie mit 1 Elter und 1 Kind;
der Bessere von Beiden wird zum Elter der nächsten Generation.
- einfachste Evolutionsstrategie mit 1 Elter und 1 Kind;
- (1,7)-ES :
- 1 Elter und 7 Kinder;
von den 7 Kindern wird das Beste zum Elter der nächsten Generation.
- 1 Elter und 7 Kinder;
+
(µ/p λ) - Evolutionsstrategie mit Rekombination
,
- Der zusätzliche Parameter p beschreibt, wie viele Eltern jeweils an der Erzeugung eines Nachkommen beteiligt sind.
- Es hat sich gezeigt, dass p<µ keine Vorteile für den Evolutionsfortschritt bringt. Die Multi-Rekombination mit p=µ erweist sich für den Praktiker als sinnvoll.
Beispiele:
- (5/2,20)-ES - 5 Eltern erzeugen insgesamt 20 Kinder:
- für die Erzeugung 1 Kindes werden jeweils 2 Eltern zufällig ausgewählt;
- die ausgewählten 2 Eltern werden jeweils rekombiniert und das entstandene Kind mutiert;
- die besten 5 Kinder werden zu Eltern der nächsten Generation.
- (4/4+10)-ES - 4 Eltern erzeugen insgesamt 10 Kinder:
- für die Erzeugung 1 Kindes werden immer alle Eltern genutzt;
- die Eltern nehmen an der Selektion für die nächste Generation teil.
Hinweis:
Die ES-Notation bietet auch Möglichkeiten zur Beschreibung geschachtelter Strategien, welche z.B. konkurrierende, zeitweilig isolierte Populationen mit einbeziehen. Das ist für den Optimierungspraktiker zur Zeit jedoch noch nicht von Bedeutung!
Konfiguration von Evolutionsstrategien
Eine optimale Konfiguration einer Evolutionsstrategie soll mit einem Minimum an Rechenzeit hinreichend stabil zu einer nutzbaren optimalen Lösung führen:
+
(µ/p λ) - Evolutionsstrategie mit Rekombination
,
- die ES mit Rekombination wird durch fünf Haupt-Parameter beschrieben:
- µ … Eltern-Anzahl
- λ … Kinder-Anzahl
- +,… Selektionsart (Überleben der Eltern)
- Typ der Rekombination (mit p = µ, da optimal!)
- Mutationsteuerung (Schrittweite incl. Regelungstyp)
Eltern-Anzahl
- Die Zahl der Eltern µ gibt vor, wie viele unterschiedliche Parametersätze nach der Selektion für die nächste Generation erhalten bleiben (Populationsgröße)
- Für hinreichend glatte Zielfunktionsoberflächen (kein Rauschen, stückweise kontinuierlich) ist 1 Elter ausreichend. Mehrere Eltern bremsen dann nur die Fortschrittsgeschwindigkeit!
- Mit der Zunahme des stochastischen Anteils der Zielfunktion sollte die Zahl der Eltern erhöht werden. Dies bewirkt eine Art Mittelwertbildung der stochastischen Zielfunktionsschwankungen über die Streubreite der selektierten Eltern.
- Mit der Zahl der Eltern muss proportional auch die Kinderzahl erhöht werden. Dies wird letztendlich durch die verfügbaren Ressourcen des Computers beschränkt. Bei rechenintensiven Simulationsmodellen wird z.B. die Rechenzeit für die Berechnung einer Generation so groß, dass dies durch den Fortschritt von Generation zu Generation nicht kompensiert wird.
- Beginnend mit einer geringeren Elternanzahl kann man diese und die zugehörige Kinder-Anzahl durch Beobachtung des Fortschritts schrittweise anpassen, um möglichst schnell die optimale Lösung zu finden.
Problem der 1. Eltern-Generation:
- ein Elter (lokales Suchverfahren):
- Es wird die Anfangslösung sofort als 1. Eltern-Generation benutzt.
- Der Optimierungsverlauf entspricht einer lokalen Suche ausgehend von der Anfangslösung.
- Die generierten Kinder streuen ausgehend von den aktuellen Elter-Mutationsschrittweiten um das Elter.
- Die Mutationsschrittweiten passen sich im Verlaufe des Optimierungsfortschritts an den Gradienten der Zielfunktion an.
- mehrere Eltern (Start als globales Suchverfahren):
- Die Anfangslösung (Startwerte) wird als ein Elter genutzt.
- Die Datensätze der zusätzlich benötigten Eltern werden im Suchraum im Sinne einer globalen Suche zufällig verteilt generiert.
- Beginnend mit diesen global verteilten Eltern der ersten Generation beginnt dann laut Konfiguration die ES mit der Generierung der Kinder und die Selektion der nächsten Eltern-Generation.
- Hierbei vergrößert sich die Gefahr, dass aus den weit von der Anfangslösung entfernt liegenden Eltern keine bewertbaren "Modell"-Kinder entstehen können. Ursachen sind z.B. physikalisch nicht realisierbare Exemplare bzw. aus Gründen der Modell-Stabilität numerisch nicht mehr berechenbaren Verhalten.
- Konvergiert die Lösung zu einem Optimum, so mündet der Prozess im Prinzip wieder in einer lokalen Suche.
Kinder-Anzahl
- Die Zahl der Kinder λ legt fest, wie viele Parameterkombinationen innerhalb des Mutations- und Rekombinationsbereiches der Eltern erzeugt werden.
- Auf die Zielfunktion bezogen ist dies praktisch die Zahl der Tastschritte um die vorhandenen Ausgangslösungen der Eltern herum.
- Für hinreichend glatte Zielfunktionen ist bereits 1 Kind ausreichend, welches im Rahmen der (1+1)-ES mit dem 1 Elter konkurriert.
- Die Anzahl der Kinder muss zumindest so groß sein, dass für die nächste Elterngeneration genügend Individuen zur Auswahl stehen.
- Das Zahlen-Verhältnis Eltern/Kinder ist ein Maß für den Selektionsdruck:
- Für glatte Zielfunktionen wird z.B. eine (1,5)-ES empfohlen.
- Um eine gleichmäßigere Konvergenz zu erreichen, kann man die Zahl der Kinder auf eine (1,10)-ES erhöhen.
- Bei Vorliegen einer verrauschten Zielfunktion bringt es keinen Effekt, allein die Zahl der Kinder zu erhöhen! Hier hilft nur eine Erhöhung der Elternzahl mit proportionaler Erhöhung der Kinderzahl.
Selektionsart (Ueberleben der Eltern)
Selektion nennt man den Vorgang, um aus der Menge alle Individuen der aktuellen Lösungspopulation die Individuen der nächsten Eltern-Generation zu bestimmen. Das Überleben der Eltern ist dabei nur der erste Schritt des Selektionsprozesses:
- In der Natur können Eltern meist über mehrere Generationen hinweg leben und Nachkommen erzeugen. Sie konkurrieren dabei mit den jeweiligen Folge-Generationen. Die Eltern sind aber nie unsterblich.
- In der Evolutionsstrategie wird dies vereinfacht. Entweder werden die Datensätze der Eltern sofort nach dem Erzeugen der Kinder vernichtet oder sie können beliebig oft an der Selektion für die nächste Elterngeneration teilnehmen:
- Komma - Eltern dürfen nicht überleben:
- Der erreichte Zielfunktionswert kann sich dabei auch verschlechtern. Dies geschieht immer dann, wenn alle Kinder schlechter sind als das beste Elternindividuum.
- Ein 'Verklemmen' der Evolutionsstrategie infolge unsterblicher Eltern wird verhindert.
- Plus - Eltern dürfen überleben:
- Da keine Verschlechterungen möglich sind, führt dies bei gutmütigen Zielfunktionen (glatt mit einem ausgeprägtem Optimum) meist zu einem schnelleren Finden des Optimums.
- Es können aber unsterbliche Eltern entstehen. Dies geschieht z.B., wenn die ebenfalls vererbte Mutationsschrittweite für die Zielfunktion viel zu groß ist und demzufolge alle Kinder zwangsläufig schlechter werden.
- Komma - Eltern dürfen nicht überleben:
Im zweiten Schritt wird dann meist eine Besten-Selektion vorgenommen:
- Die verbliebene Population wird nach Ihrem Fitness-Wert sortiert.
- Die besten µ Individuen werden danach als neue Eltern-Generation benutzt.
Rekombinationstypen
Ziel der Rekombination ist es, gute Eigenschaften verschiedener Eltern auf ein Kind zu übertragen:
- Es wurde mathematisch nachgewiesen, dass die Rekombination einen Anteil zur Fortschrittsgeschwindigkeit der ES beisteuert (Siehe: Rechenberg - Vorlesung Evolutionsstrategie II - Kapitel 5)
- Ab zwei Eltern sollte die Multi-Rekombination angewandt werden, da die Rekombination der Datensätze aller Eltern immer einen größeren Evolutionsfortschritt bringt (in OptiY automatisch realisiert).
Es existieren verschiedene Ansätze, wie die Datensätze der Eltern zum Kinderdatensatz zusammengeführt werden, z.B.:
- diskrete Multi-Rekombination
- Der Datensatz eines Kindes entsteht durch zufällige Kombination der Datensätze aller Eltern. Z.B. steuert Elter1 die Wert einer Länge, Elter5 den Wert eines Durchmessers, Elter3 den Wert einer Dicke usw. bei. Die Kinderdatensätze liegen bei der diskreten Multi-Rekombination auf der Oberfläche einer Hyperkugel um den Schwerpunkt der Elterndatensätze.
- Durch die anschließende Mutation der rekombinierten Datensätze wird die Oberfläche dieser Hyperkugel normalverteilt aufgeweitet.
- Mittelwertbildung
- Der Datensatz eines Kindes entsteht aus den Mittelwerten der kombinierten Elternwerte.
- Die Kinder-Datensätze werden anschließend mutiert.
- kontinuierliche Verteilungen (z.B. Gleich, Normal, Rampe)
- Der Datensatz eines Kindes entsteht aus "Zufallswerten" entsprechend der gewählten Verteilungsfunktion zwischen den beteiligten Elternwerten.
- Diese Zufallswerte werden anschließend noch mutiert.
- diskrete Multi-Rekombination
- Multi-Rekombination bedeutet immer Beteiligung aller Eltern bei der Erzeugung eines Kindes.
- Einfache Rekombination würde zufällig zwei Eltern aus der Elternmenge auswählen.
Mutationssteuerung
Die richtige Anpassung der Mutationsschrittweite an die lokale Topologie der Zielfunktion ist das A und O zur Erzielung eines möglichst guten Optimierungsfortschritts.
A. Art der Schrittweitenregelung
- Multischritt-Option:
für jede Optimierungsvariable wird eine separate Streubreite (Mutationsschrittweite) vererbt, so dass Anpassungen an richtungsabhängige Steigungen der Zielfunktion möglich sind. - Einzelschritt-Option:
gemeinsamer Betrag der Mutationsschrittweite für alle Optimierungsvariablen wird vererbt, so ist die Anpassungen an richtungsabhängige Steigungen der Zielfunktion nicht mehr möglich.
- Multischritt-Option:
B. Ermittlung der aktuellen Mutationsschrittweite
- Mittelwert:
- Im Sinne der Multi-Rekombination wird die Mutationsschrittweite für jede Optimierungsvariable des Kindes als Mittelwert der zugehörigen Eltern-Schrittweiten gebildet.
- Damit werden bei verrauschten Zielfunktionen stochastische Fluktuationen der Mutationsschrittweite vermindert, da die Anzahl der Eltern eine integrierende, glättende Wirkung auf die Änderung der Schrittweite ausübt.
- Der gebildete Mittelwert wird anschließend mutiert (normalverteilt aufgeweitet).
- Bestwert:
- Es wird jeweils die Schrittweite des besten Eltern-Individuums übernommen.
- Dieser Wert wird danach ebenfalls mutiert.
- Mittelwert:
- Mutation der Mutationsschrittweite:
- Sowohl bei Mittel- als auch bei Bestwert-Nutzung wird zusätzlich eine globale Mutationsschrittweite an jedes Kind vererbt.
- Diese globale Schrittweite wird bei jedem Kind über einen auf 1 normierten Zufallsfaktor "mutiert".
- Die Mutation der einzelnen Mutationsschrittweiten erfolgt bei jedem Kind mit der individuellen globalen Mutationsschrittweite.
- Mutation der Mutationsschrittweite:
- Wichtig:
Da die Mutationsschrittweiten mit vererbt und selektiert werden, erfolgt eine Optimierung dieser Schrittweiten in Hinblick auf einen schnellen Fortschritt.
C. Das Evolutionsfenster
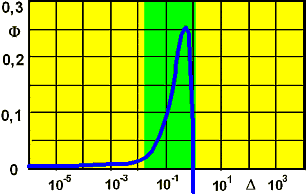
- Bei der ungeschlechtlichen Vermehrung wird z.B. die Fähigkeit zur hinreichend schnellen Anpassung an sich verändernde Bedingungen wesentlich durch die Mutationsrate bestimmt:
- Wird der Einfluss des Zufalls gering gehalten (z.B. durch Reparaturmechanismen), so entstehen fast gleiche Kinder und die Möglichkeit einer schnellen Veränderung ist gering.
- Wird die Mutationsrate sehr groß, so sind die meisten Kinder so stark geschädigt, dass sie keine Fortpflanzungschance haben (nicht funktionieren!).
- Es existiert in Abhängigkeit von der Umwelt (zu der auch die anderen Mitglieder der eigenen Population gehören) immer eine optimale Mutationsrate, welche den schnellsten Entwicklungsfortschritt erlaubt. Den Bereich um die optimale Mutationsrate, der zu einem Entwicklungsfortschritt führt, nennt man auch Evolutionsfenster:
- Die Mutationsrate gehört zur Evolutionsstrategie auf unterstem Niveau. Darüber liegen dann die Strategien der Rekombination von Genen mittels geschlechtlichen Fortpflanzung oder Gentransfer.
- Für die Mutationsrate existiert eine Codierung im Genotyp, die ebenfalls der Evolution unterworfen ist. Die momentan bessere Fitness ist auch ein Resultat der besseren Evolutionsstrategie.
- Die momentane Mutationsrate als Teil der Evolutionsstrategie wird mit vererbt. Praktisch erfolgt damit eine Schrittweitenregelung, welche die Mutationsschrittweite an die lokale Topologie der Zielfunktion anpasst.
- 1/5-Erfolgsregel:
- Der Quotient aus den erfolgreichen Mutationen (also Mutationen, die eine Verbesserung der Fitness bewirken) zu allen Mutationen sollte etwa ein Fünftel betragen. Dann befindet sich der Evolutionsprozess im Evolutionsfenster.
- Diese Regel kann die Grundlage für eine Anpassung der Mutationsschrittweite bilden. Ist der Quotient >1/5, so sollte die Varianz der Mutationen erhöht werden, bei einem kleineren Quotienten sollte sie verringert werden.
- Infolge der Einbeziehung der Mutationsschrittweite in den Optimierungsprozess stellt sich diese automatisch so ein, dass sich der Prozess innerhalb des Evolutionsfensters befindet.
Co-Evolutionaere Strategien
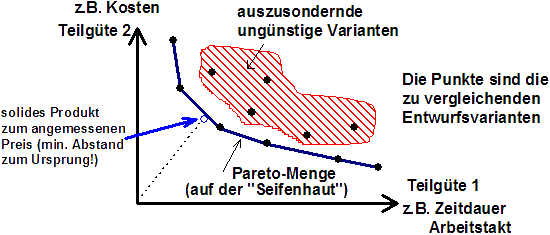
Die Prinzipien der Evolutionsstrategien sind auch nutzbar, um Problemstellungen der Mehrkriterien-Optimierung zu lösen, wie sie in den Grundlagen zur Optimierung beschrieben sind:
Das grundlegende Konzept co-evolutionärer Algorithmen basiert auf Ökosystemen mit stark wechselwirkenden Populationen verschiedener Arten (Coevolution):
- Co-Evolution ist der Antrieb für die ständige Weiterentwicklung der Arten innerhalb von Ökosystemen auch bei stabilen Umweltbedingungen.
- Die Prinzipien der Co-Evolution kann man für die Mehrkriterien-Optimierung nutzen, indem man die normale Evolutionsstrategie erweitert.
- Dazu wird speziell die wechselseitige Anpassung von Räuber- und Beutetieren nachgebildet (schnellere Hasen sind von Nachteil für die Füchse und umgekehrt):
- Der Wettbewerb existiert nicht nur innerhalb einer Art, sondern auch zwischen den co-existierenden Arten.
- In den Fitnesswert eines Individuums muss auch die Fitness der jeweils anderen Art einfließen - die Räuber-Fitness wächst mit verminderter Beute-Fitness und umgekehrt.
Ein Kunstgriff zur Nutzung der Co-Evolution für die Mehrkriterien-Optimierung kann darin bestehen, die Gewichtungsfaktoren der Teilgüten als Optimierungsvariablen der sogenannten Co-Individuen zu definieren:
- Beutetiere: Individuen (Parametersätze) der aktuellen Population von Lösungen.
- Räuber: Zusätzliche Population von Co-Individuen, welche die wertende Sicht der Nutzer auf die zu optimierende Lösung verkörpern:
- Die Gewichtsfaktoren der Teilgüten stellen die Optimierungsvariablen der Räuber dar.
- Diese Gewichtsfaktoren können sich damit ausgehend von einem vorgegebenen Anfangswert durch die Evolutionsstrategie verändern.
- Die Summe aller Gewichtungsfaktoren jedes Räubers bleibt konstant =1 (Randbedingung).
- Die Gesamt-Güte jeder Lösung ("Beutetier") wird durch die benutzten Gewichtsfaktoren für die Teilgüten bestimmt. Die Güte einer Lösung ist also Nutzerabhängig, da jeder Nutzer ("Räuber") eigene Gewichtsfaktoren besitzt:
- Um an alle Lösungen (Individuen) einen einheitlichen Maßstab anzulegen, werden die Gewichtsfaktoren des besten Co-Individuums (der vorherigen Generation) benutzt. Damit widerspiegelt die berechnete Fitness der aktuellen Lösungen die Anpassung an den bisherigen besten Räuber:
- Der Fitness-Wert eines Co-Individuums ("Räubers") wird mittels seiner eigenen Gewichtsfaktoren und den Teilgüten des besten Individuums (beste Lösung der vorherigen Generation) berechnet:
- Ein Räuber ist umso besser, je schlechter in Hinblick auf seine Eigenschaften (Wi) die zur Zeit bestangepasste Beute erscheint. Dies widerspiegelt sich im negativen Vorzeichen nach der Summenbildung.
- Der Bezug auf die vorherige Generation erfolgt aus Vereinfachungsgründen, weil sich die Fitness-Werte innerhalb der aktuellen Generation wechselseitig bedingen.
- Die Population der Lösungen ("Beutetiere") driftet zur Pareto-Menge. Die unterlegte "normale" Evolutionsstrategie bevorzugt Lösungen in Richtung dieser Pareto-Menge.
- Das Prinzip der wechselseitigen Anpassung zwischen Individuen und Co-Individuen führt zu endlosen Schwingungen entlang der Pareto-Menge.
Hinweis: Im OptiY ist ein abgewandelter Algorithmus implementiert!