Software: OptiY-Workflow - Einfache Toleranzkette: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
<div align="center">'''Autoren:''' [http://www.ifte.de/mitarbeiter/nagel.html '''Dr.-Ing. PD Thomas Nagel'''], [http://www.ifte.de/mitarbeiter/kamusella.html ''' Dr.-Ing. Alfred Kamusella'''] </div> | <div align="center">'''Autoren:''' [http://www.ifte.de/mitarbeiter/nagel.html '''Dr.-Ing. PD Thomas Nagel'''], [http://www.ifte.de/mitarbeiter/kamusella.html ''' Dr.-Ing. Alfred Kamusella'''] </div> | ||
<div align="center">'''Dieser Beitrag wird gerade erstellt und ist unvollständig!''' </div> | <div align="center">'''Dieser Beitrag wird gerade erstellt und ist noch unvollständig!''' </div> | ||
== Aufgabenstellung == | |||
Am Beispiel einer einfachen Maßkette soll gezeigt werden, welche neuen Möglichkeiten die probabilistische Simulation im Vergleich zu klassischen, analytischen Methoden eröffnet: | Am Beispiel einer einfachen Maßkette soll gezeigt werden, welche neuen Möglichkeiten die probabilistische Simulation im Vergleich zu klassischen, analytischen Methoden eröffnet: | ||
Version vom 27. Juni 2008, 14:12 Uhr
Dieser Beitrag wird gerade erstellt und ist noch unvollständig!
Aufgabenstellung
Am Beispiel einer einfachen Maßkette soll gezeigt werden, welche neuen Möglichkeiten die probabilistische Simulation im Vergleich zu klassischen, analytischen Methoden eröffnet:
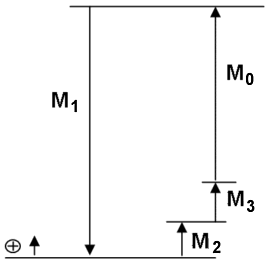
Das Schlussmaß M0 ergibt sich aus der Gesamt-Abmessung Ma abzüglich der Teilmaße Mb und Mb.
Vorgegeben:
- zulässige Toleranz T0 des Schlussmaßes M0 (unter Montage- und Funktionsaspekten):
- T0= 0,4 (obere Grenze!)
- als Ausgangslösung stehen folgende Maße in der Maßkette:
- Ma= 11,8-0,2
- Mb= 1,3-0,1
- Nc= 1,5±0,05
- diese Ausgangslösung besitzt die Nennmaße Ni mit Toleranzmittenabmaßen Eci und Toleranzen Tci:
- Na= 11,8 / Eca=-0,1 / Ta=0,2
- Nb= 1,3 / Eca=-0.05 / Tb=0,1
- Nc= 1,5 / Eca=0 / Tc=0,1
Gesucht:
- das Nennmaß des Schlussmaßes N0
- Toleranzmittenabmaß des Schlussmaßes Ec0
- eine Aussage, ob die geforderte Toleranz des Schlussmaßes mit der Ausgangslösung eingehalten wird.
- günstigere Toleranzen für die Maßglieder der Toleranzkette, um die zulässige Toleranz des Schlussmaßes eventuell voll auszuschöpfen.
Workflow-Modell der Maßkette
Maxima-Minima-Methode
Diese Methode berücksichtigt bei der Berechnung der Schlussmaß-Toleranz die Worst-Case-Fälle und gewährleistet damit eine 100%-ige Einhaltung des Schlussmaßes. Zum gleichen Ergebnis gelangt man mit der probabilistischen Simulation einer Maßkette, wenn man jedes Maß als gleichverteilt betrachtet. Damit liegen alle einzelnen Ist-Maße innerhalb ihres vorgegebenen Toleranz-Bereiches.