Startseite: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung |
||
| (20 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<div align="center">'''''Wenn zwei Knaben jeder einen Apfel haben und sie diese Äpfel tauschen,'''''</div> | <div align="center">'''''Wenn zwei Knaben jeder einen Apfel haben und sie diese Äpfel tauschen,'''''</div> | ||
<div align="center">'''''hat am Ende auch nur jeder einen.'''''</div> | <div align="center">'''''hat am Ende auch nur jeder einen.'''''</div> | ||
| Zeile 7: | Zeile 5: | ||
<div align="center">---</div> | <div align="center">---</div> | ||
<div align="center">''Platon (ca. 427 v.Chr.-347 v.Chr.)''</div> | <div align="center">''Platon (ca. 427 v.Chr.-347 v.Chr.)''</div> | ||
=== Simulationen erzeugen Interpretationen der Welt=== | === Simulationen erzeugen Interpretationen der Welt=== | ||
Für Techniker oder Wissenschaftler ist es inzwischen Alltag, sich an Ergebnissen numerischer Simulationen zu erfreuen oder sich über Probleme beim Erstellen der erforderlichen numerischen Modelle zu ärgern. <br />In vielen Bereichen funktionieren die Modelle zuverlässig, man denke nur an das rechnergestützte Konstruieren (CAD). Probleme mit der Modellgenauigkeit und numerischen Stabilität gibt es jedoch nicht nur bei der Wettervorhersage. Diese Probleme treten überall auf, wo die nichtlinearen Effekte komplexer Systeme mathematisch behandelt werden sollen. | Für Techniker oder Wissenschaftler ist es inzwischen Alltag, sich an Ergebnissen numerischer Simulationen zu erfreuen oder sich über Probleme beim Erstellen der erforderlichen numerischen Modelle zu ärgern. <br />In vielen Bereichen funktionieren die Modelle zuverlässig, man denke nur an das rechnergestützte Konstruieren (CAD). Probleme mit der Modellgenauigkeit und numerischen Stabilität gibt es jedoch nicht nur bei der Wettervorhersage. Diese Probleme treten überall auf, wo die nichtlinearen Effekte komplexer Systeme mathematisch behandelt werden sollen. Erschwerend wirkt weiterhin, dass fast alle Parameter realer Systeme keine exakten Werte besitzen, sondern nur über statistische Verteilungsfunktionen beschreibbar sind: | ||
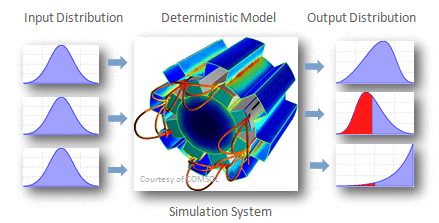
<div align="center">[[Bild:Titelbild_Probabilistische_Simulation.gif| ]]</div> | |||
=== Numerische Optimierung wird die Welt verändern=== | === Numerische Optimierung wird die Welt verändern=== | ||
| Zeile 16: | Zeile 13: | ||
=== OptiYummy - denn Optimieren darf Spaß machen!=== | === OptiYummy - denn Optimieren darf Spaß machen!=== | ||
Leider sind solche Idealfälle bei der Anwendung der numerischen Optimierung nicht die Regel. Im Normalfall fehlt dem Nutzer noch das erforderliche Methodenwissen und er kämpft mit einer Vielzahl numerischer Probleme.<br />OptiYummy soll Technikern und Wissenschaftlern den Einstieg in diese neue Technologie erleichtern, indem die Grundlagen zur numerischen Optimierung hier in möglichst leicht verständlicher und anwendbarer Form dargestellt werden. Ein Schwerpunkt ist dabei die Robust-Optimierung durch Einbeziehung der Parameter-Streuungen mittels probabilistischer Simulation.[[Bild:Logo-ifte.gif|left|IFTE]] | Leider sind solche Idealfälle bei der Anwendung der numerischen Optimierung nicht die Regel. Im Normalfall fehlt dem Nutzer noch das erforderliche Methodenwissen und er kämpft mit einer Vielzahl numerischer Probleme.<br />OptiYummy soll Technikern und Wissenschaftlern den Einstieg in diese neue Technologie erleichtern, indem die Grundlagen zur numerischen Optimierung hier in möglichst leicht verständlicher und anwendbarer Form dargestellt werden. Ein Schwerpunkt ist dabei die Robust-Optimierung durch Einbeziehung der Parameter-Streuungen mittels probabilistischer Simulation. <br /> <div align="right">'''Hoffentlich gelingt es!'''</div> | ||
[[Bild:Logo-ifte.gif|left|IFTE]] | |||
[ | [https://www.ifte.de ''Institut für Feinwerktechnik und Elektronik-Design (IFTE)''] <br /> | ||
der Technischen Universität Dresden<br /> | der Technischen Universität Dresden<br /> | ||
in Zusammenarbeit mit [ | |||
<br />in Zusammenarbeit mit [https://www.optiy.eu ''OptiY GmbH''] <br /> | |||
[[Bild:Banner-optiy.gif|left|OptiY]] | [[Bild:Banner-optiy.gif|left|OptiY]] | ||
Aktuelle Version vom 21. Dezember 2018, 16:56 Uhr
Simulationen erzeugen Interpretationen der Welt
Für Techniker oder Wissenschaftler ist es inzwischen Alltag, sich an Ergebnissen numerischer Simulationen zu erfreuen oder sich über Probleme beim Erstellen der erforderlichen numerischen Modelle zu ärgern.
In vielen Bereichen funktionieren die Modelle zuverlässig, man denke nur an das rechnergestützte Konstruieren (CAD). Probleme mit der Modellgenauigkeit und numerischen Stabilität gibt es jedoch nicht nur bei der Wettervorhersage. Diese Probleme treten überall auf, wo die nichtlinearen Effekte komplexer Systeme mathematisch behandelt werden sollen. Erschwerend wirkt weiterhin, dass fast alle Parameter realer Systeme keine exakten Werte besitzen, sondern nur über statistische Verteilungsfunktionen beschreibbar sind:
Numerische Optimierung wird die Welt verändern
Auch bei hinreichend validierten und numerisch stabilen Modellen scheitert der Mensch an der Komplexität der nichtlinearen Wechselwirkungen. Eine zielgerichtete Veränderung von Parametern, um ein gewünschtes Verhalten zu erreichen, ist mit "gesundem Menschenverstand" dann meist unmöglich.
Hier können die modernen Verfahren der numerischen Optimierung helfen. Der Mensch beschreibt im Idealfall, welche Ziele er erreichen möchte und der Computer findet dafür eine optimale Lösung.
OptiYummy - denn Optimieren darf Spaß machen!
Leider sind solche Idealfälle bei der Anwendung der numerischen Optimierung nicht die Regel. Im Normalfall fehlt dem Nutzer noch das erforderliche Methodenwissen und er kämpft mit einer Vielzahl numerischer Probleme.
OptiYummy soll Technikern und Wissenschaftlern den Einstieg in diese neue Technologie erleichtern, indem die Grundlagen zur numerischen Optimierung hier in möglichst leicht verständlicher und anwendbarer Form dargestellt werden. Ein Schwerpunkt ist dabei die Robust-Optimierung durch Einbeziehung der Parameter-Streuungen mittels probabilistischer Simulation.

Institut für Feinwerktechnik und Elektronik-Design (IFTE)
der Technischen Universität Dresden
in Zusammenarbeit mit OptiY GmbH